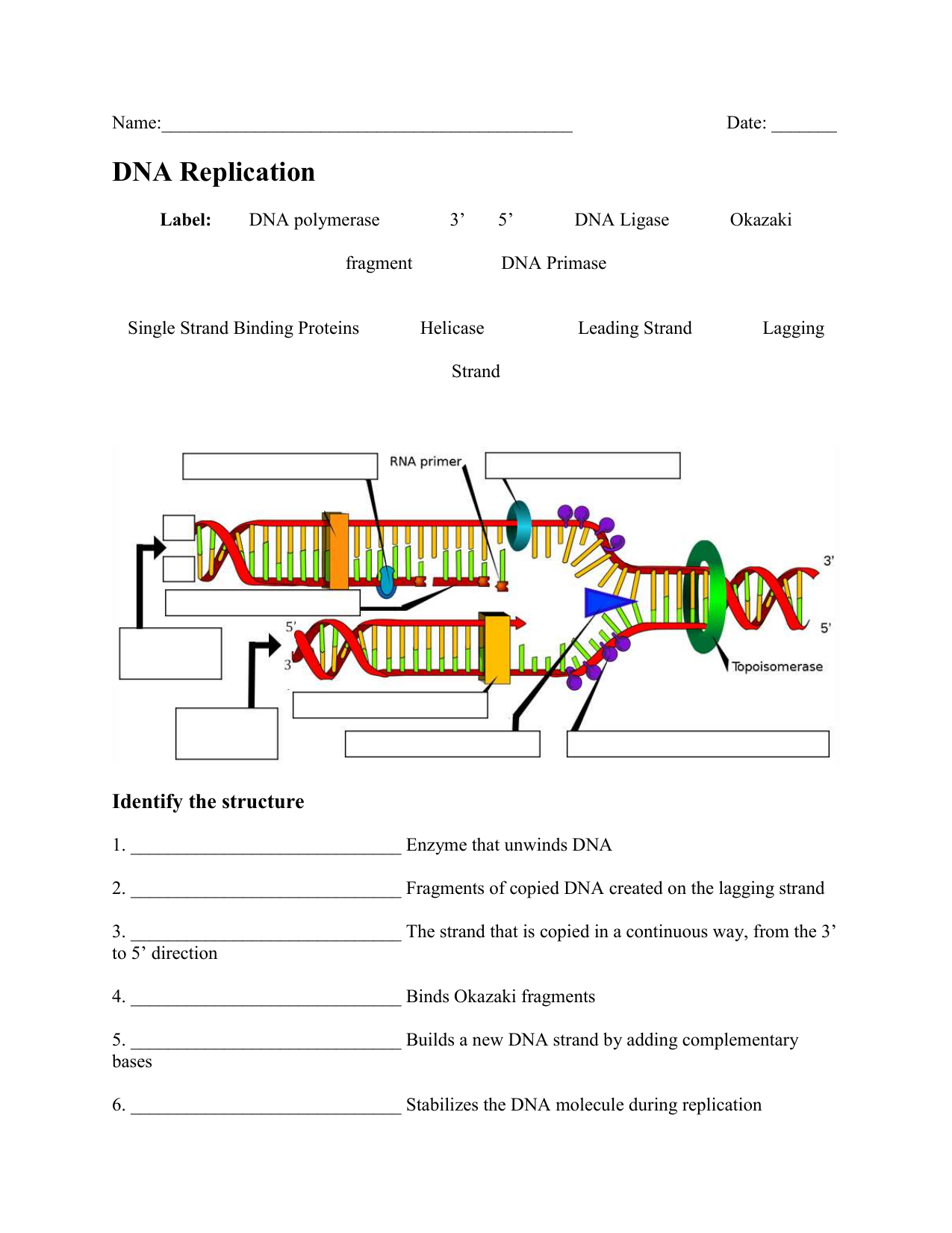
Master Fractions with Engaging Mixed Numbers Worksheets

In the quest for mathematical proficiency, mixed numbers often represent a pivotal concept for learners. Understanding these fractions, which combine whole numbers and proper fractions, not only enriches a student's fraction knowledge but also paves the way for more complex mathematical operations. This post aims to provide a detailed guide on how to master mixed numbers using thoughtfully crafted worksheets and strategies.
Understanding Mixed Numbers

Mixed numbers are a special type of fraction that consists of:
- A whole number part.
- A fractional part where the numerator is less than the denominator, making it a proper fraction.
For example, 3 1⁄2, 7 3⁄4, or 11 1⁄8 are all mixed numbers. They are written as a whole number followed by a fraction with a space in between.
Converting Between Improper Fractions and Mixed Numbers

To convert an improper fraction to a mixed number, follow these steps:
- Divide the numerator by the denominator to find the whole number part. Keep the remainder as your new numerator.
- The original denominator remains unchanged.
- Combine the whole number and the new fraction with a space in between.
📝 Note: To convert a mixed number back to an improper fraction, multiply the whole number by the denominator, then add the numerator of the fractional part to get the new numerator. The denominator remains the same.
Adding and Subtracting Mixed Numbers

Adding or subtracting mixed numbers involves several steps:
- When denominators match: Simply add or subtract the numerators, keeping the whole number part separate, then adjust if the fraction goes over one whole.
- When denominators differ:
- Convert the mixed numbers to improper fractions.
- Find a common denominator.
- Add or subtract the numerators, then simplify the resulting fraction.
- Convert the result back to a mixed number if necessary.
Multiplication and Division of Mixed Numbers

Here’s how to approach multiplication and division with mixed numbers:
- Multiplication: Convert the mixed numbers to improper fractions, then multiply as with regular fractions, and simplify.
- Division: Again, convert to improper fractions. Invert the divisor (turn it upside down), then multiply, and simplify the result.
Engaging Mixed Numbers Worksheets
Here are some ways to create engaging worksheets that will enhance students’ understanding of mixed numbers:
| Worksheet Type | Description |
|---|---|
| Conversion Puzzles | Puzzles where students convert improper fractions to mixed numbers or vice versa in a fun, puzzle-like format. |
| Story Problems | Real-life scenarios involving mixed numbers to make the learning practical and interesting. |
| Math Drills | Timed exercises focused on speed and accuracy in performing operations with mixed numbers. |
| Visual Aids | Worksheets with diagrams or charts to help students visualize mixed numbers and their operations. |
| Mixed Number Bingo | A game that combines learning with fun, where students match fractions and mixed numbers to numbers on their bingo card. |

📚 Note: Always tailor the complexity of the worksheets to the students' current understanding, gradually introducing more complex scenarios.
By now, we've covered the fundamentals of mixed numbers, provided strategies for conversions, operations, and the design of engaging worksheets. Here are a few crucial points to remember:
- Understanding mixed numbers is key to mastering fractions and advancing in math.
- Converting between improper fractions and mixed numbers is essential for simplifying calculations.
- Worksheets should be engaging, varied, and aligned with the student's skill level to ensure effective learning.
How do you convert a mixed number to an improper fraction?

+
To convert a mixed number to an improper fraction, multiply the whole number by the denominator of the fraction, then add the numerator. This new value becomes the numerator of the improper fraction, with the denominator remaining the same.
Why are mixed numbers useful in real-life scenarios?

+
Mixed numbers are useful because they provide a clearer representation of quantities that are larger than one but not whole. For instance, measuring lengths, cooking (like 1 1⁄2 cups of sugar), or even financial situations (2 1⁄4 loans) where it’s more practical to show the whole and the fraction separately.
What are the best practices for teaching mixed numbers?

+
Start with visual aids to help students conceptualize the idea, gradually introduce operations, use real-life contexts to explain the relevance, and incorporate interactive and varied activities like games and puzzles to keep engagement high. Also, always review conversions frequently to solidify understanding.