5 Quick Tips for Mastering Fraction to Decimal Worksheets

In today's digital age, where proficiency in mathematics is more crucial than ever, understanding how to convert fractions to decimals is a fundamental skill that can benefit students, professionals, and anyone dealing with numbers in their daily life. Whether you're tackling complex equations or simply ensuring your budget calculations are accurate, mastering fraction to decimal conversion can streamline your mathematical processes. Here are five quick tips to master fraction to decimal worksheets, ensuring you become adept at this vital arithmetic operation.
Understand the Basics

Before diving into the complexities of fraction to decimal conversion, it’s imperative to grasp the underlying principles:
- Fraction to Decimal Conversion: A fraction represents a part of a whole, where the numerator (top number) shows how many parts we have, and the denominator (bottom number) indicates into how many equal parts the whole has been divided.
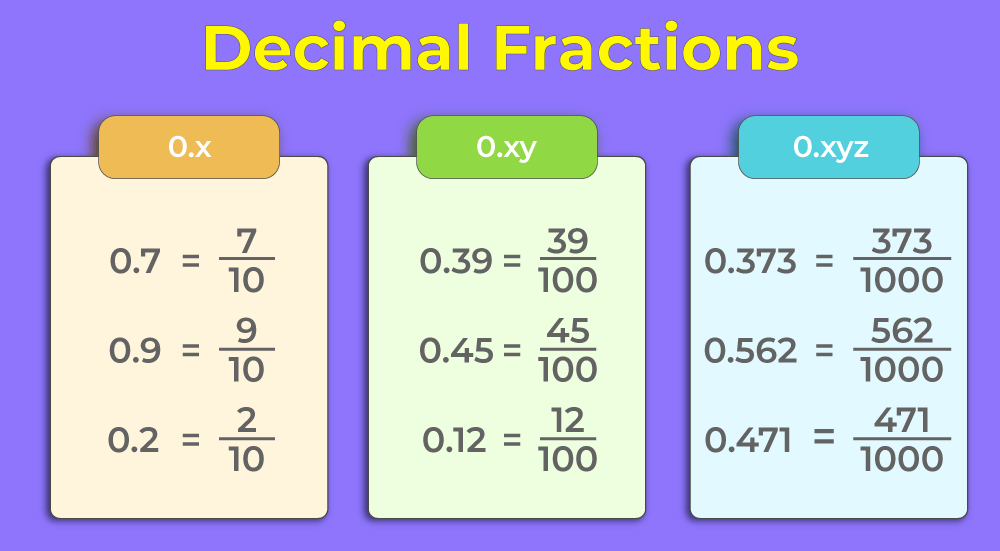
- Decimal Representation: Decimals are another way of writing fractions with a denominator of 10, 100, 1000, etc.
💡 Note: The relationship between fractions and decimals is foundational; understanding one helps in understanding the other.
Employ Long Division
The most straightforward method to convert fractions to decimals involves long division:
- Set up the division problem where the numerator is divided by the denominator.
- Perform the division until you get a result, which could be a terminating decimal or a repeating decimal. Here’s how:
| Example | Steps | Result |
|---|---|---|
| 3⁄4 | Divide 3 by 4 | 0.75 (terminating) |
| 1⁄3 | Divide 1 by 3 | 0.333… (repeating) |

Recognize Common Conversions
Certain fractions convert into decimals easily, and recognizing these can save time:
- 1⁄2 = 0.5
- 1⁄4 = 0.25
- 1⁄8 = 0.125
Getting acquainted with these common conversions can make the process of working with fractions much quicker.
Utilize Mental Math for Simplicity

Mastering mental math tricks can significantly enhance your speed in fraction to decimal conversion:
- Dividing by 2: Simply halve the numerator for halves and quarters.
- Dividing by 5: Multiply the numerator by 2 and then divide by 10 for easy conversions.
- Dividing by 10: Move the decimal point one place to the left.
These tricks work particularly well when dealing with simple fractions or when time is of the essence.
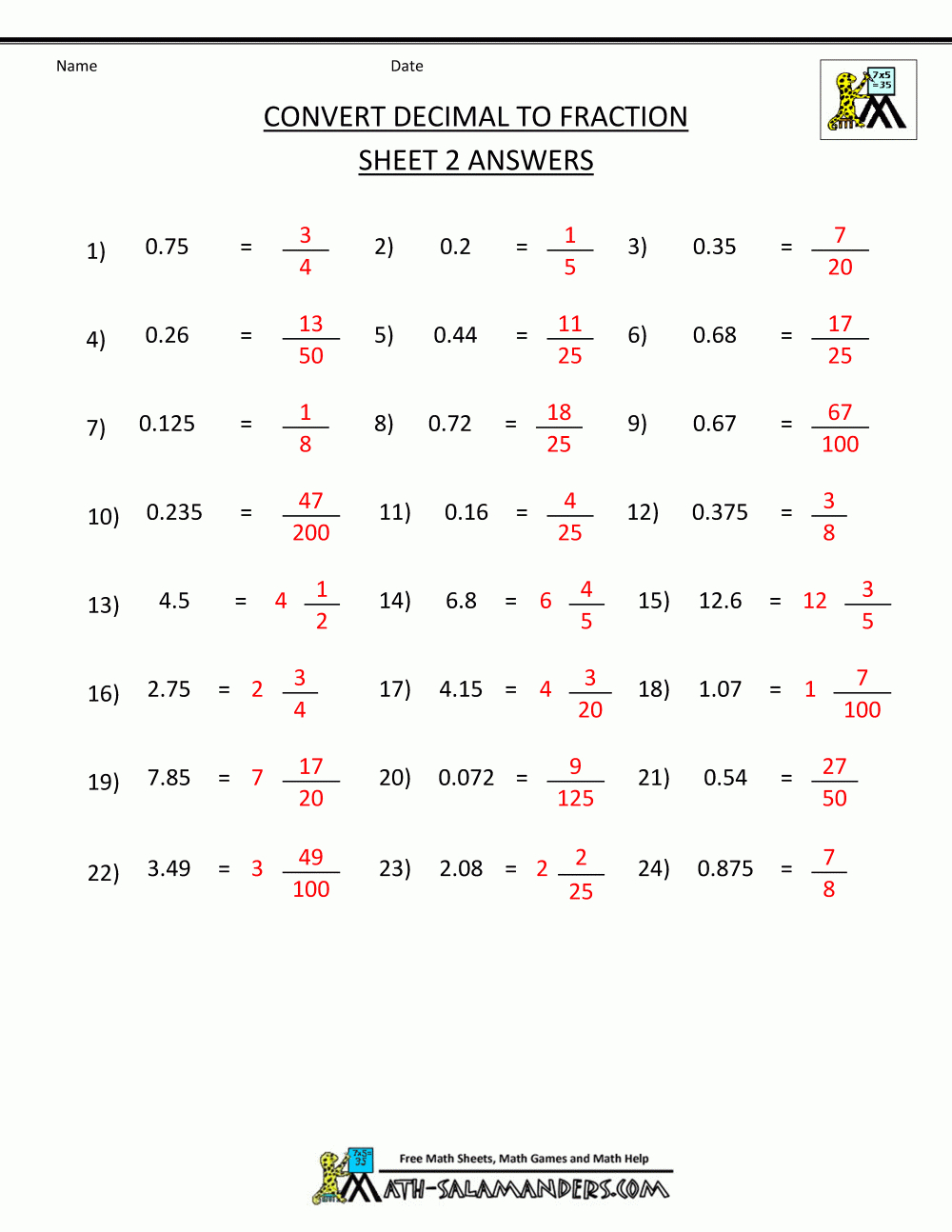
Practice Regularly with Worksheets

The key to mastering any skill is consistent practice. Here’s how you can practice:
- Worksheet Selection: Choose worksheets that challenge your current skill level, from basic to advanced problems.
- Time Yourself: Use a timer to assess how long it takes to complete a set of conversions, aiming to reduce this time gradually.
- Review and Correct: After completing a worksheet, review your work, identify common errors, and understand why they occurred to prevent them in the future.
Regular practice with varying difficulty levels will not only reinforce your conversion skills but also build your confidence in handling any fraction to decimal problem.
By following these five quick tips, you're well on your way to mastering fraction to decimal worksheets. Converting fractions to decimals becomes less of a chore and more of a straightforward mathematical operation you can perform with ease. Keep practicing, be mindful of common conversions, and leverage mental math techniques for faster results. Over time, you'll find this skill becoming second nature, allowing you to solve mathematical problems with increased efficiency.
What’s the best method to memorize common fraction to decimal conversions?

+
The best method involves regular repetition and integration into everyday activities. Flashcards, quizzes, and applying the conversions in practical scenarios can reinforce your memory.
Can a fraction have more than one decimal representation?

+
No, a fraction has one unique decimal representation. For example, 1⁄2 can only be 0.5 and not any other value.
How can I check if my fraction to decimal conversion is correct?

+
You can check by converting the decimal back to a fraction. If the fraction you get matches the original, the conversion was correct.
Is there a way to convert repeating decimals back to fractions?

+
Yes, there are methods like setting up equations to solve for repeating decimals or using algebraic techniques to revert the decimal back to its original fraction form.
Why should I learn to convert fractions to decimals?

+
Understanding this conversion is crucial for accuracy in math, engineering, finance, and everyday calculations where decimals provide a clearer picture of quantities.



