Master Dividing Whole Numbers by Fractions with Our Worksheet
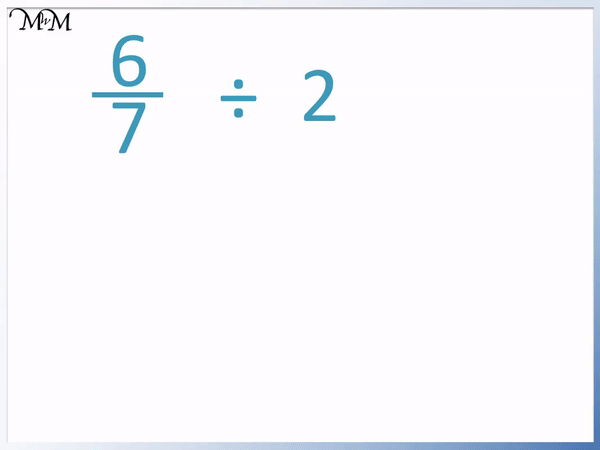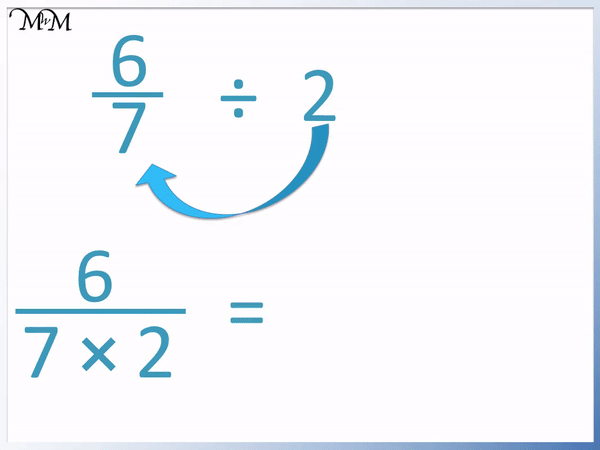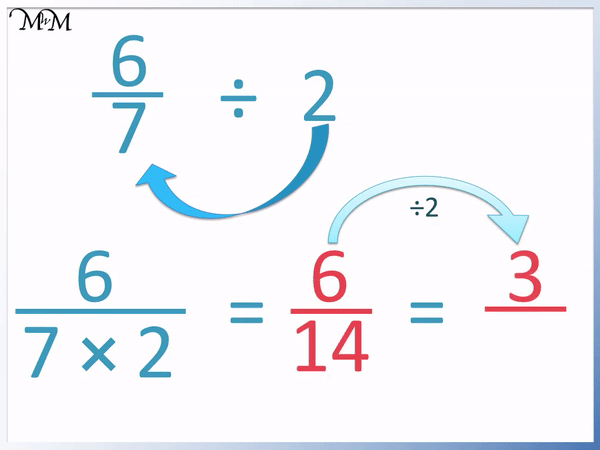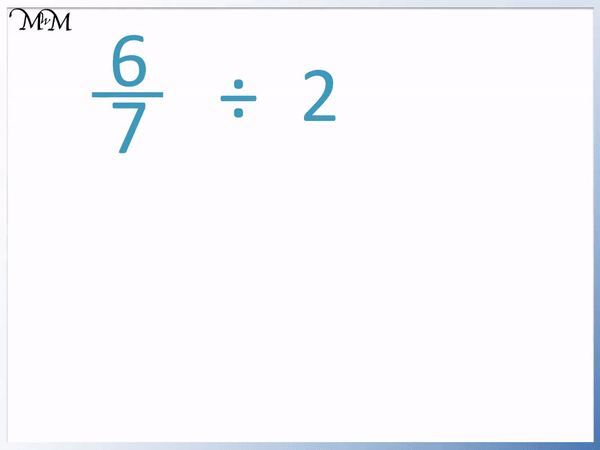
Teaching math concepts, especially those involving fractions and whole numbers, can be a daunting task. However, our worksheet on "Dividing Whole Numbers by Fractions" simplifies this process, making it both accessible and engaging. This blog post will guide you through the steps to effectively use our worksheet, offer some math teaching strategies, and enhance your understanding of how dividing by fractions works.
Understanding the Basics of Division with Fractions

Before delving into the worksheet, let's briefly revisit why dividing by fractions might confuse some students. Traditionally, when we divide by a number, we make pieces smaller. However, with fractions, we're dividing by something smaller than 1, which, counterintuitively, results in a larger number:
- A whole number divided by a fraction bigger than 1 results in a smaller number.
- A whole number divided by a fraction smaller than 1 results in a bigger number.
How Does Division by Fractions Work?

Here's the rule: Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped over. For example, the reciprocal of 3/4 is 4/3. So, if you want to divide 6 by 3/4, you multiply 6 by 4/3, resulting in 8. Here's how it goes:
6 ÷ 3/4 = 6 * 4/3 = 24/3 = 8
Maximizing the Worksheet: A Comprehensive Guide

Preparation for Teaching

Before you dive into the worksheet:
- Ensure students have a solid grasp of basic multiplication and division with whole numbers.
- Introduce the concept of reciprocals and illustrate with examples.
Worksheet Structure and Content

Our worksheet is structured to build students' confidence step-by-step:
- Simple Division: Starting with whole numbers divided by unit fractions like 1/2, 1/3.
- Intermediate Division: Progressing to dividing by proper fractions such as 2/3, 3/4.
- Challenge Division: Tackle whole numbers divided by mixed numbers, like 4 ÷ 1 1/2.
Guiding Students Through the Worksheet

- Start with clear instructions. Show them how to rewrite the division as a multiplication by the reciprocal.
- Encourage them to write down each step to understand the process.
- Have students verbalize their thought process to reinforce understanding.
- Use real-life scenarios or visual aids to illustrate the division by fractions.
Practical Examples
Here’s a visual aid to illustrate the concept:

Assessing Students’ Work

When marking, look for:
- Correct conversion from division to multiplication by the reciprocal.
- Accurate calculations in both the numerator and denominator.
- Proper handling of mixed numbers and reducing fractions when necessary.
🎓 Note: Ensure students have space to work out their solutions to avoid confusion with other steps or crowded sheets.
Strategies for Teaching Division by Fractions

- Analogies and Visuals: Use pie charts or segmented pizzas to show parts of wholes.
- Building a Number Sense: Guide students to understand why dividing by a fraction makes the result larger.
- Word Problems: Help students relate division to everyday situations to make it more tangible.
- Peer Learning: Group work can be very effective for sharing strategies and understanding.
- Reinforcement: Use software or online platforms for additional practice.
💡 Note: Encourage students to explore different strategies to find what works best for them.
Wrapping Up

The journey of teaching division by fractions through our worksheet has shown us various ways to approach this concept. By starting with the basics, gradually introducing complexity, and using a variety of teaching strategies, we provide students with a well-rounded understanding. Remember, the goal is not just to solve the problems but to understand why these mathematical operations work. Encourage persistence and continuous learning, as math is a skill that develops over time.
Why does dividing by a fraction make the result larger?

+
Dividing by a fraction is equivalent to multiplying by its reciprocal, which, in many cases, results in a larger number because you’re multiplying by a value greater than 1.
Can you give me a real-life example of dividing whole numbers by fractions?

+
Sure! If you have 10 apples and you need to divide them among 1⁄2 of the people, you’re effectively giving 10 apples to each person, making the division result in 20 apples per person (10 ÷ 1⁄2 = 10 * 2 = 20).
How can I help my students remember the rule for dividing by fractions?

+
Use mnemonic devices like “KCF” (Keep, Change, Flip) where you keep the first fraction, change the division to multiplication, and flip the second fraction.