Master Fraction, Decimal, and Percent Conversions Easily

The mastery of converting between fractions, decimals, and percentages is not just a basic mathematical skill; it's a fundamental tool for practical applications in everyday life, including financial literacy, cooking, and even data analysis. Understanding these conversions allows individuals to better manage their money, interpret nutritional labels, analyze statistics, or even complete household DIY projects with precision. In this post, we delve into the techniques for effortless conversion, ensuring you can transition smoothly between these numerical representations.
Understanding the Basics

Fractions, decimals, and percentages all represent parts of a whole, but they do so in different ways:
- Fractions: Represented as one number over another, like ( \frac{1}{4} ), indicating a part divided by the whole.
- Decimals: Numbers that extend beyond the decimal point, like 0.25, showing parts of a whole as tenths, hundredths, etc.
- Percentages: A special type of fraction where the denominator is always 100, expressed as 25%, for instance.
Converting Fractions to Decimals


The process of converting a fraction to a decimal involves:
- Divide the numerator (top number) by the denominator (bottom number).
- For example, ( \frac{3}{4} ) becomes ( 3 \div 4 = 0.75 ).
Converting Decimals to Fractions


The steps to convert a decimal to a fraction are as follows:
- Take the decimal number, remove the decimal point, and write it as the numerator.
- Count the number of decimal places as the power of 10 for the denominator.
- So, 0.75 would become ( \frac{75}{100} ), which simplifies to ( \frac{3}{4} ).
Converting Percentages to Decimals and Fractions
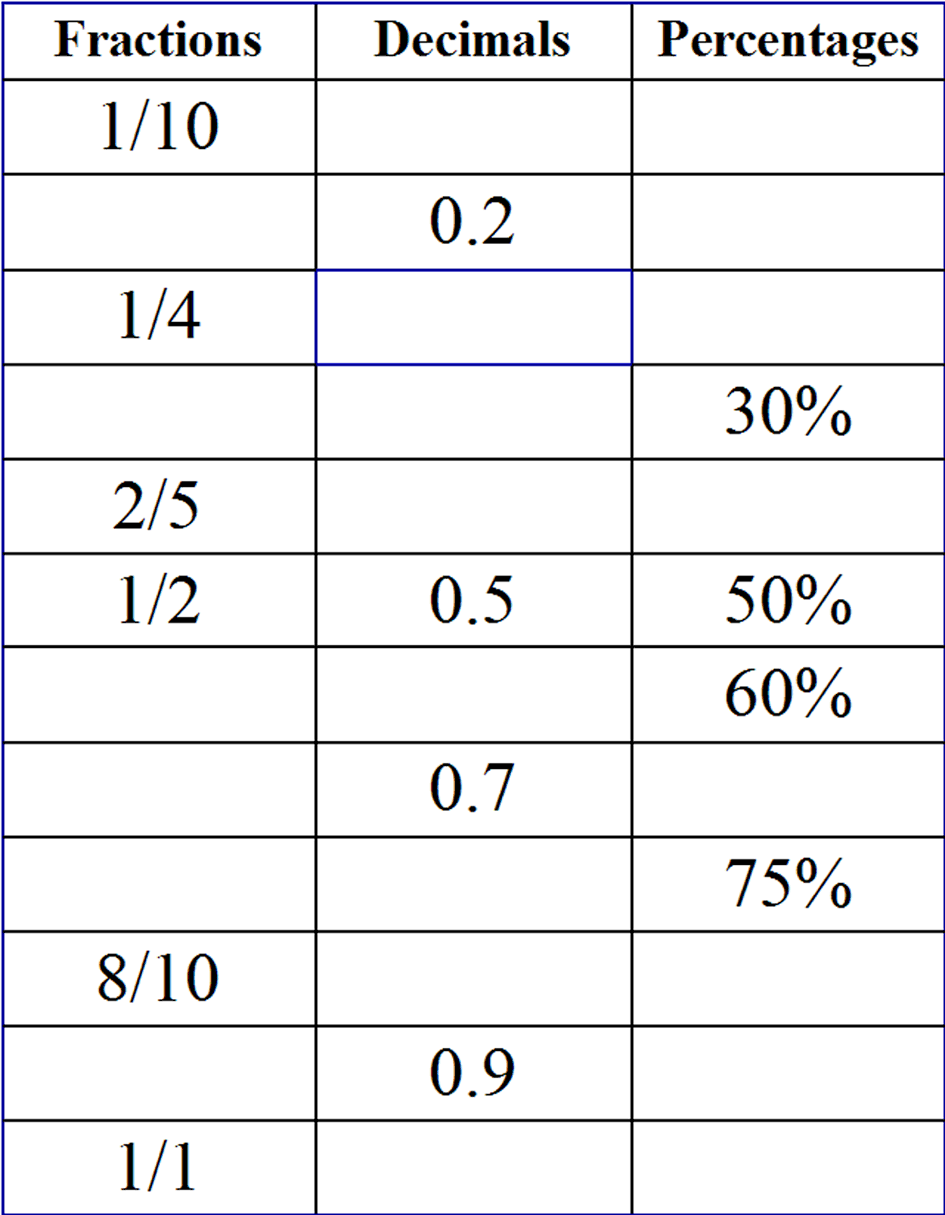

To convert a percentage to a decimal or fraction:
- Divide the percentage by 100 to get the decimal, like 25% becomes 0.25.
- For fractions, you’re converting ( \frac{25}{100} ), which simplifies to ( \frac{1}{4} ).
Practical Applications

Conversions between these forms are used in:
- Financial Calculations: When dealing with interest rates, discounts, taxes, or tips.
- Cooking: Recipes often list ingredients in fractions or percentages, requiring conversion for accurate measurements.
- Data Analysis: Statistics and surveys use percentages to represent data, requiring conversions for visualization and comparison.
- DIY Projects: Precise measurements are needed for cutting, mixing materials, etc.
Let's consider some practical examples:
| Situation | Original Number | Conversion |
|---|---|---|
| Shopping Discount | 25% off | 0.25 or \frac{1}{4} off |
| Mixing Ingredients | 3/4 cup of flour | 0.75 cup or 75% of the total |
| Statistical Data | 52% Approval | 0.52 or \frac{52}{100} , simplifies to \frac{13}{25} |

🔍 Note: Simplify your fractions whenever possible to keep your math straightforward.
In summary, the ability to convert effortlessly between fractions, decimals, and percentages not only aids in mathematical computations but also serves as an invaluable skill in various real-world scenarios. By mastering these conversions, you'll be better equipped to handle the complexities of financial transactions, culinary measurements, and data interpretation, fostering a deeper understanding and application of numerical concepts.
Why is it important to learn about conversions?
+
Understanding conversions between different numerical forms (fractions, decimals, and percentages) enables clearer communication of quantitative information and is crucial for accurate calculations in everyday applications, from financial analysis to culinary arts and beyond.
Can converting numbers be done automatically?

+
Yes, there are many online calculators and software tools that can perform these conversions automatically, but understanding the process manually is beneficial for quick mental conversions and to comprehend how these tools work.
What should I do if a decimal has a repeating pattern?

+
Repeating decimals can be represented as fractions by recognizing their repeating sequence. For example, ( 0.\overline{3} ) (which means 0.3 repeating) can be expressed as ( \frac{1}{3} ). There are specific techniques to convert such decimals to fractions, like multiplying by a power of 10 to remove the decimal point and then subtract the original number.


