Master Parallel Lines with Easy Proof Worksheets

Understanding parallel lines is fundamental in geometry and it forms the basis for much of the analytical reasoning required in math. Not only do they enhance our understanding of spatial relationships, but they also are crucial in various real-world applications like engineering, architecture, and even in computer graphics. In this extensive guide, we'll delve into parallel lines, explore their proofs, and provide you with worksheets to practice and solidify your understanding.
What Are Parallel Lines?

Parallel lines refer to two lines within the same plane that do not intersect at any point. Here are some key points about parallel lines:
- They maintain a constant distance from each other, known as the perpendicular distance.
- They never meet, which means they have no points in common.
- They can be vertical or horizontal on a plane but must not share any angle.
Understanding Parallel Line Proofs
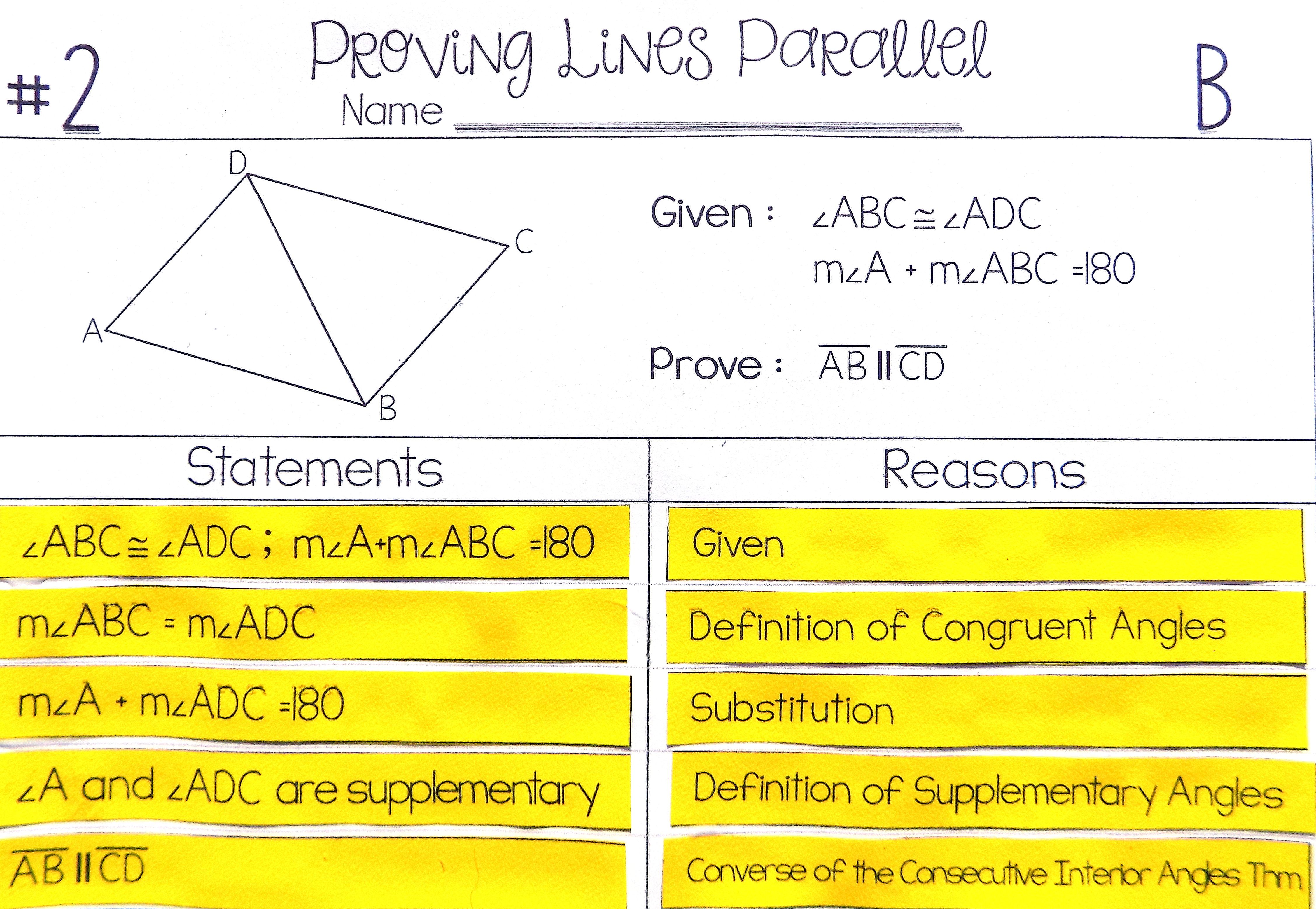
Proving that lines are parallel involves demonstrating that certain conditions hold true. These conditions often involve angles formed when a transversal cuts through the lines. Here are the main methods:
1. Converse of the Corresponding Angles Postulate

If two lines are cut by a transversal so that the corresponding angles are congruent, then the lines are parallel.
2. Converse of the Alternate Interior Angles Theorem

If two lines are cut by a transversal so that alternate interior angles are congruent, then the lines are parallel.
3. Converse of the Same-Side Interior Angles Theorem

If two lines are cut by a transversal so that same-side interior angles are supplementary, then the lines are parallel.
Here's a simple example to illustrate:
| Method | Condition |
|---|---|
| Corresponding Angles | If ∠1 ≅ ∠2, then lines are || |
| Alternate Interior Angles | If ∠3 ≅ ∠4, then lines are || |
| Same-Side Interior Angles | If ∠5 + ∠6 = 180°, then lines are || |

Practicing Parallel Line Proofs with Worksheets

To master parallel line proofs, practicing with worksheets is invaluable. Here's how you can effectively use worksheets:
- Identify Angles: Label all angles formed by the transversal and parallel lines.
- Use Properties: Apply the properties of parallel lines to deduce which angles are congruent or supplementary.
- Set Up Proofs: Construct logical arguments based on these properties.
📚 Note: Not all worksheets provide answers; solving without solutions helps develop critical thinking.
Benefits of Practicing with Proof Worksheets

Engaging with proof worksheets offers several benefits:
- Enhances Problem-Solving Skills: Regular practice improves your ability to analyze geometric relationships.
- Builds Confidence: Successfully proving lines are parallel boosts your confidence in geometry.
- Prepares for Advanced Math: This foundational knowledge is critical for advanced math topics like trigonometry and calculus.
- Reinforces Visual-Spatial Skills: Working with lines and angles improves spatial awareness.
Worksheet Design and Usage

When creating or using parallel line proof worksheets, consider the following:
Structure

- Diagrams: Clearly drawn with labeled angles for clarity.
- Questions: Progress from simple to more complex proofs.
- Hints and Steps: Sometimes provide partial proofs to guide learners.
Sample Problems

Here are some exercises you might encounter:
- Prove that line L is parallel to line M if ∠1 and ∠2 are supplementary.
- Given ∠A ≅ ∠B, show that lines X and Y are parallel.
📝 Note: Using varied diagrams helps learners recognize patterns across different setups.
In summary, mastering parallel lines involves understanding their definitions, recognizing the angles formed by transversals, and being adept at proving these relationships through logical arguments. Worksheets serve as an excellent tool to reinforce this knowledge, offering practical exercises that challenge and solidify your understanding of these geometric principles. Whether you're a student, teacher, or enthusiast, the consistent practice of parallel line proofs will enhance your mathematical thinking and prepare you for more complex geometry topics.
Why are parallel lines important in geometry?

+
Parallel lines are fundamental because they help in understanding spatial relationships, form the basis for various geometric theorems, and are applicable in real-world scenarios where maintaining constant distances or avoiding intersections is crucial.
Can lines that look parallel on paper be parallel in real space?
+
Not always. In Euclidean geometry, lines can be proved parallel if they meet certain conditions, but in non-Euclidean spaces, such visual parallels might not hold true.
How can I use parallel line properties in real life?

+
Architects use parallel lines to ensure stability in building structures, engineers design roads and tracks with parallel lines to avoid collisions, and graphic designers use them for aesthetic and functional design.

