Master Percentages Easily: Percent of a Number Worksheet

Understanding Percentages: An Essential Skill for Everyday Life

Percentages are an integral part of our daily lives, from calculating discounts while shopping to understanding tax rates, and even gauging progress in personal goals. This blog post will guide you through the process of mastering percentages, particularly in the context of finding the percent of a number, a skill that can be incredibly useful in a variety of real-world scenarios.
The Basics of Percentages

Before diving into the specifics, let’s clarify what percentages are. A percentage, denoted by the symbol %, represents a number or ratio expressed as a fraction of 100. Here are some key points:
- A percentage can be calculated by dividing a number by 100.
- For example, 50% means 50 out of 100, or 0.5 when expressed as a decimal.
Finding the Percent of a Number

Here’s how you can find the percent of any number:
Step-by-Step Process:

- Identify the percentage: Let’s say you want to find 25% of a number.
- Convert the percentage to a decimal: Divide by 100. So, 25% becomes 0.25.
- Multiply: Multiply the decimal by the number in question. If the number is 80, then 0.25 x 80 = 20. Hence, 25% of 80 is 20.
Common Percentage Calculations:

To make life easier, here are some common percentages and their decimal equivalents:
| Percentage | Decimal |
|---|---|
| 1% | 0.01 |
| 10% | 0.10 |
| 25% | 0.25 |
| 50% | 0.50 |
| 100% | 1.00 |

💡 Note: These values can make mental calculations much quicker!
Practical Applications

Percentages aren’t just a math concept; they’re practically everywhere:
- Finance: Interest rates, loans, and investment returns.
- Health: BMI calculations, nutritional values.
- Statistics: Polling, survey analysis, and data interpretation.
- Sales: Calculating discounts, commissions, and VAT.
Worksheet Practice for Mastery

To become proficient in percentages, consistent practice is crucial. Here are some worksheets that can help:
- Basic Percentage Problems: Practice finding percentages of given numbers.
- Converting Between Forms: Exercises on converting between percentages, fractions, and decimals.
- Application Problems: Real-life scenarios where you apply percentage calculations.
Advanced Techniques

Proportional Reasoning:
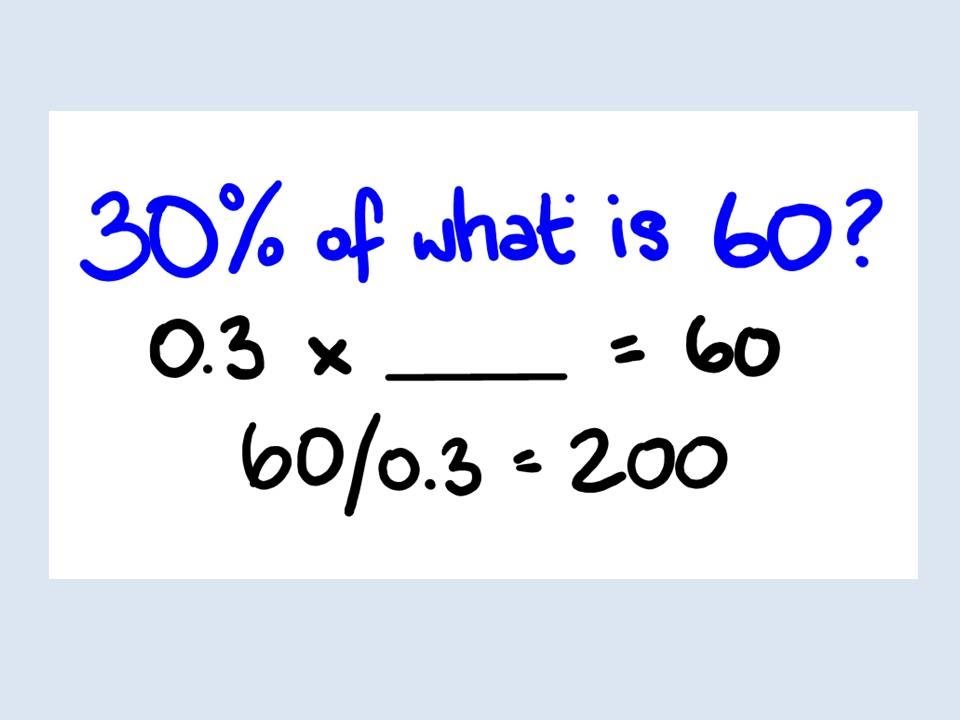
If you know one part of a percentage and need the other, use the concept of proportion:
If x% of a number A is B, then A/B = 100/x. This formula helps in solving a wide range of percentage problems.
Estimating Percentages:
Many times, precise calculations aren’t necessary; estimation can be handy:
- Round numbers up or down to the nearest tens or hundreds for quicker computations.
- Use fractions when percentage values are common. For example, 50% is the same as a half, 25% is a quarter, etc.
💡 Note: Learning these shortcuts can significantly speed up your problem-solving abilities.
Wrapping Up

Mastering percentages is not just about memorizing formulas or methods; it’s about understanding the concept and applying it to real-life situations. From everyday financial decisions to academic problem-solving, percentages play a critical role. By engaging with practice worksheets, employing quick estimation techniques, and understanding advanced applications, you can become adept at manipulating percentages to your advantage.
Having a solid grasp of percentages means you can:
- Confidently make informed financial decisions.
- Calculate discounts and savings with ease.
- Interpret data and statistics more accurately.
This knowledge empowers you in both personal and professional spheres, equipping you to navigate through various quantitative challenges with confidence and precision.
How can I find 15% of 200 without a calculator?

+
You can mentally calculate 10% of 200, which is 20. Then, since 15% is half of 10% plus another 10%, you add half of 20 (which is 10) to 20 to get 15% of 200, equalling 30.
Why are percentages important in finance?

+
Percentages are fundamental in finance for calculating interest rates, determining investment growth or loss, understanding tax implications, and figuring out loan repayments, among other uses.
Can percentages be over 100%?

+
Absolutely, percentages can exceed 100%. For example, a 200% increase means doubling the original value, which is essentially a growth of 100% from the base plus another 100%.



