5 Ways to Ace Factoring Ax2 Bx C Worksheets
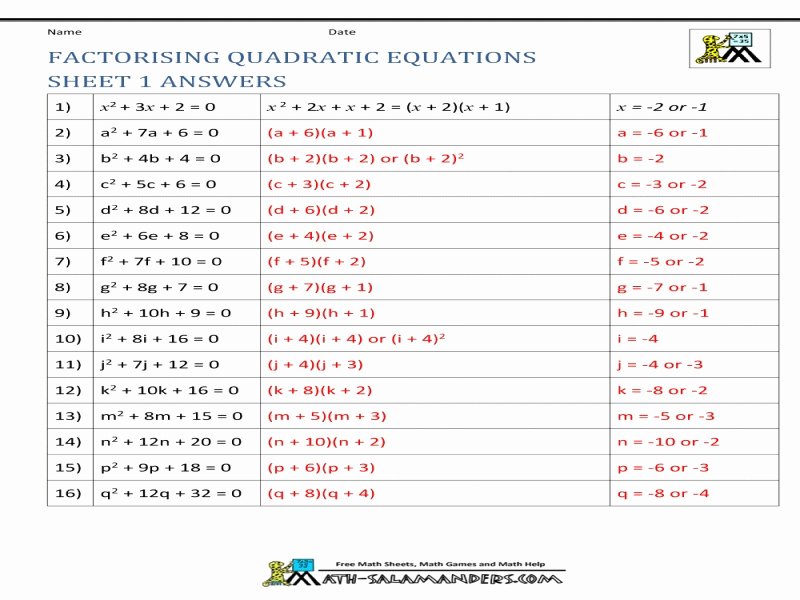
Whether you're a student tackling algebra or an educator trying to assist in your students' understanding of quadratic equations, mastering factoring ax2 + bx + c worksheets can be a pivotal skill. Factoring is not just a step in solving quadratic equations; it's a bridge to understanding more complex algebraic concepts. Here are five strategies to ensure success in factoring, ensuring both effectiveness and efficiency.
Understanding the Basics

Before you dive into the depths of factoring, it’s crucial to grasp the fundamental concepts:
- Factoring Definition: Factoring is the process of breaking down an expression into its prime factors, or its constituent parts.
- Polynomials: Recognize that ax2 + bx + c is a polynomial, and its roots are the solutions to when it equals zero.
- Quadratic Trinomials: Learn to identify trinomials in the form of ax2 + bx + c, where a, b, and c are constants.
Image showcasing a quadratic trinomial can be placed here
Mastering the Box Method

The box method, or area model, helps visually break down the polynomial into simpler factors:
- Draw a box with four cells.
- Fill in the cells with the product of a * c and factors of b that when added, equal b.
- Group the factors in a way that allows you to factor by grouping.
- Factor out common terms to find the factors of the polynomial.
✅ Note: Practice with various values of a, b, and c will make you more adept with this method.
Using the AC Method

The AC method leverages the relationship between the coefficients:
- Multiply a by c (the constant term).
- Find two numbers that multiply to ac and add up to b.
- Factor the middle term using these numbers.
- Group terms to factor out common factors.
🔎 Note: The AC method is useful when the polynomial does not factor easily by inspection.
Implementing the Quadratic Formula

The quadratic formula, x = (-b ± √(b2 - 4ac)) / (2a), can be your backup plan:
- It’s particularly handy for non-factorable quadratics.
- Practice using it to understand how it relates to factoring.
- It’s a quick check for potential errors in factoring.
Practicing with Real-World Problems

Applying factoring to real-world scenarios can solidify your understanding:
- Projectile Motion: Use factoring to determine when an object will hit the ground.
- Area and Perimeter: Factor to find unknown dimensions of shapes.
- Optimization Problems: In business, understand when to maximize or minimize functions.
| Strategy | When to Use |
|---|---|
| Box Method | When polynomial is factorable and you need a visual aid. |
| AC Method | When the polynomial does not factor easily by inspection. |
| Quadratic Formula | As a last resort or to double-check your factoring work. |
| Real-World Problems | To understand the practical implications of factoring. |

Each of these strategies enhances your factoring prowess. The key to acing factoring ax2 + bx + c worksheets is consistent practice, understanding of the methods, and recognizing when to apply each technique. Remember, the path to algebraic mastery involves not just solving but also deeply understanding the underlying principles.
Why is factoring important in algebra?

+
Factoring is essential in algebra because it allows you to solve equations, simplify expressions, and understand the structure of polynomials. It’s foundational for more advanced algebraic concepts like polynomial division and calculus.
What do I do if I can’t factor a quadratic equation?

+
If you can’t factor a quadratic equation by standard methods, use the quadratic formula to find the roots directly or check for prime polynomials (those that can’t be factored over the integers).
How can real-world problems help in understanding factoring?

+
Real-world problems provide context, showing why factoring is useful. For example, factoring can help determine when a projectile will hit the ground, how to optimize manufacturing processes, or understand financial investments.


