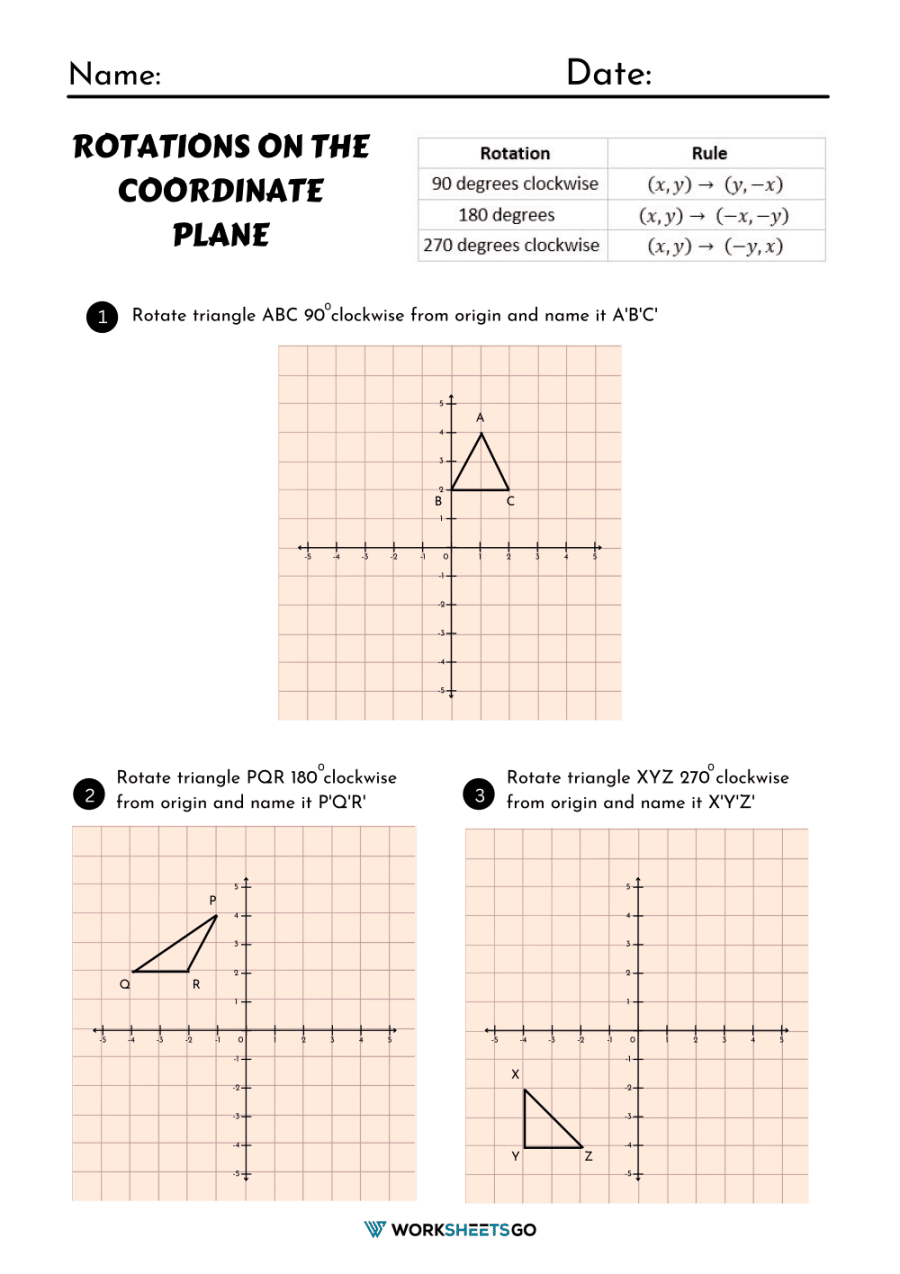
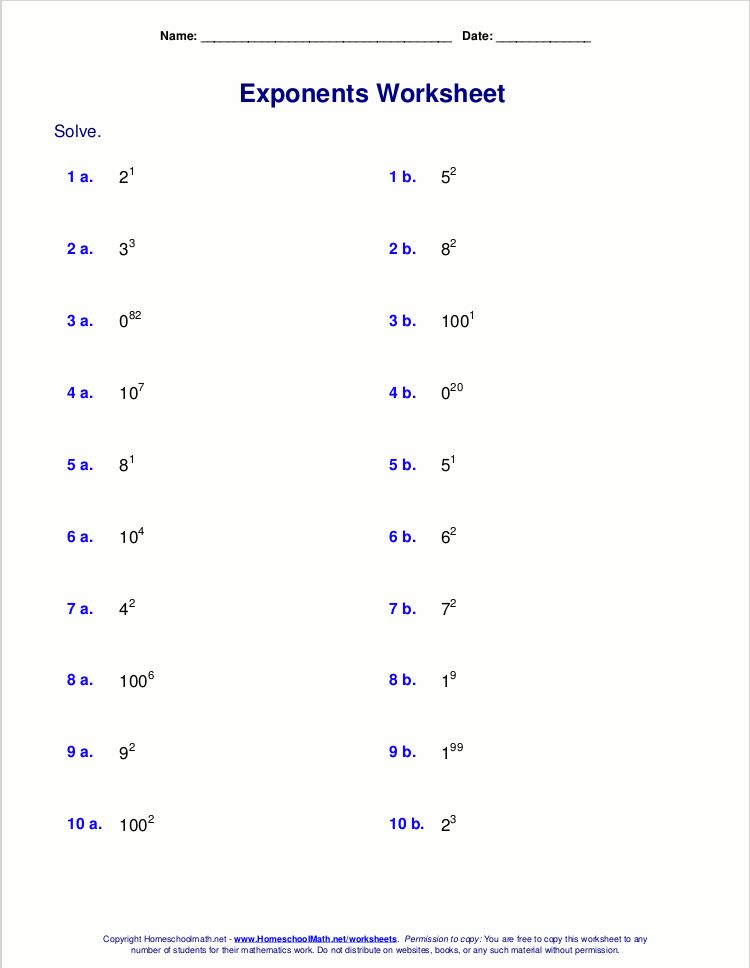
Exponent Rules Worksheet Answers: Simplify Your Learning

Understanding exponent rules is crucial in mathematics, as they provide the foundation for handling complex algebraic expressions and solving equations with ease. This guide walks you through the key exponent rules, presents practical examples, and includes a comprehensive worksheet to help solidify your understanding.
Exponent Rules: The Basics

Here are the fundamental rules you need to know:
- Product Rule:
(a^m * a^n) = a^(m + n) - Quotient Rule:
(a^m / a^n) = a^(m - n) - Power of a Power:
(a^m)^n = a^(m * n) - Power of a Product:
(a * b)^m = a^m * b^m - Power of a Quotient:
(a / b)^m = a^m / b^m - Zero Exponent:
a^0 = 1 (a ≠ 0) - Negative Exponent:
a^(-n) = 1 / a^n - Exponents with Fractional Bases:
(a/b)^n = a^n / b^n
🔍 Note: It's essential to remember that these rules apply when the base is the same in operations like multiplication and division.
Examples of Exponent Rules in Action

Let's explore each rule with examples:
Product Rule Example

Given
(x^3 * x^5), apply the product rule:x^3 * x^5 = x^(3+5) = x^8Quotient Rule Example
To simplify
(x^10 / x^7), use the quotient rule:x^(10-7) = x^3Power of a Power Example

If you need to simplify
(x^4)^2, apply the power rule:(x^4)^2 = x^(4*2) = x^8Power of a Product Example

For
(2y)^3, distribute the exponent:(2y)^3 = 2^3 * y^3 = 8y^3Power of a Quotient Example

For
(3/4)^2, distribute the exponent to both terms:(3/4)^2 = 3^2 / 4^2 = 9/16Zero Exponent Example

Any non-zero number raised to the power of zero equals one:
7^0 = 1Negative Exponent Example

When dealing with negative exponents:
5^(-3) = 1/5^3 = 1/125
By practicing these rules with different numbers and variables, you can become proficient in simplifying complex expressions.
Exponent Rules Worksheet

To practice, here is a worksheet:
| Expression | Simplify |
|---|---|
| (3^2 * 3^3) | 3^5 |
| (2/3)^2 | 4/9 |
| (x^6)^3 | x^18 |
| 7^0 | 1 |
| 6^(-2) | 1/36 |

📝 Note: Always check your answers by back-substituting to ensure your simplification is correct.
Tips for Mastering Exponent Rules

- Practice Regularly: Repetition is the key to mastery in exponent rules.
- Understand each rule: Go beyond memorization by understanding why each rule works.
- Check for Common Mistakes: Look out for errors like misapplying negative exponents or not considering fractional bases correctly.
In summary, this guide has explored the basics of exponent rules, given you plenty of examples to practice, and provided a worksheet for further practice. By understanding these rules, you're well on your way to simplifying algebraic expressions with confidence. Remember, the key to mastering these rules is consistent practice, understanding the logic behind each rule, and avoiding common pitfalls. Whether you're preparing for an exam or working on real-life problems, these exponent rules will be invaluable in your mathematical journey.
Why is understanding exponent rules important?

+
Exponent rules are essential because they simplify the manipulation of numbers in powers, making mathematical operations faster and easier to understand. They are foundational in algebra, calculus, and many scientific fields.
How do I remember all these rules?

+
Practice is crucial. Create flashcards, use mnemonics, and engage with problems that require applying these rules. Over time, they become second nature.
Can I apply these rules to fractional or negative exponents?

+
Absolutely! Fractional exponents introduce roots, while negative exponents indicate a reciprocal. Understanding how these rules interact with these types of exponents is fundamental for advanced math.