Exponential Functions Worksheet Answers: Quick Evaluation Guide

In the realm of mathematics, understanding exponential functions is pivotal for students aiming to excel in various mathematical applications, ranging from algebra to calculus and beyond. These functions are not only fundamental in theoretical mathematics but also play a crucial role in real-life scenarios involving growth rates, decay processes, and financial calculations. This blog post serves as a comprehensive guide to evaluating your understanding of exponential functions through a series of worksheet answers. Here, we will explore definitions, properties, transformations, and applications of exponential functions, providing insights into quick and effective evaluation methods.

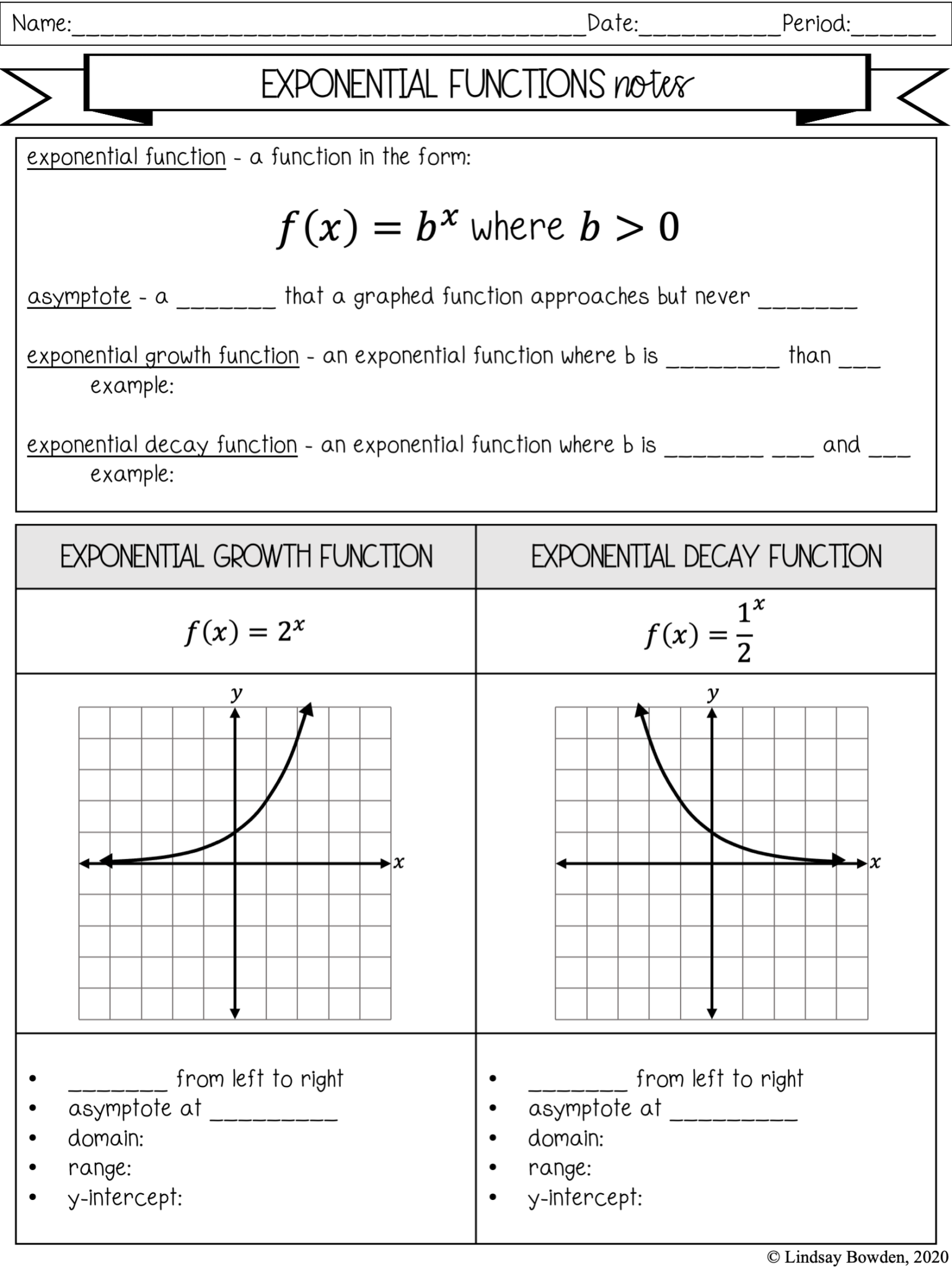
Understanding Exponential Functions

Exponential functions are mathematical expressions where the variable appears as an exponent. The general form of an exponential function is:

f(x) = a * b^x

• a represents the initial value or the amplitude of the function.
• b is the base, which must be positive and not equal to 1. If b > 1, the function models exponential growth; if 0 < b < 1, it represents exponential decay.
• x is the exponent, which can be any real number.

Properties of Exponential Functions

Here are some essential properties:

• Domain: The set of all real numbers, R.
• Range: If a > 0, the range is (0, ∞).
• The function is one-to-one, making it invertible.
• The function crosses the y-axis at a.
• The graph of f(x) never touches the x-axis; it either approaches it or infinity.

Worksheet Evaluation Guide

Here are several questions from a typical worksheet on exponential functions, along with quick evaluation answers:

Basic Understanding

1. Identify the Base

Given the function f(x) = 2 * 3^x, identify the base of the exponential growth:

Answer: The base here is 3.

2. Determine the Growth or Decay

Classify the function g(x) = 0.5^x+1 as growth or decay:

Answer: Since 0.5 < 1, this represents exponential decay.

Transformations

3. Horizontal and Vertical Shifts

Consider the function h(x) = 2^x-2 + 3. Describe the transformation:

• The function has been shifted right 2 units (h(x) = 2^x-2)
• It has also been shifted up 3 units (adding 3).

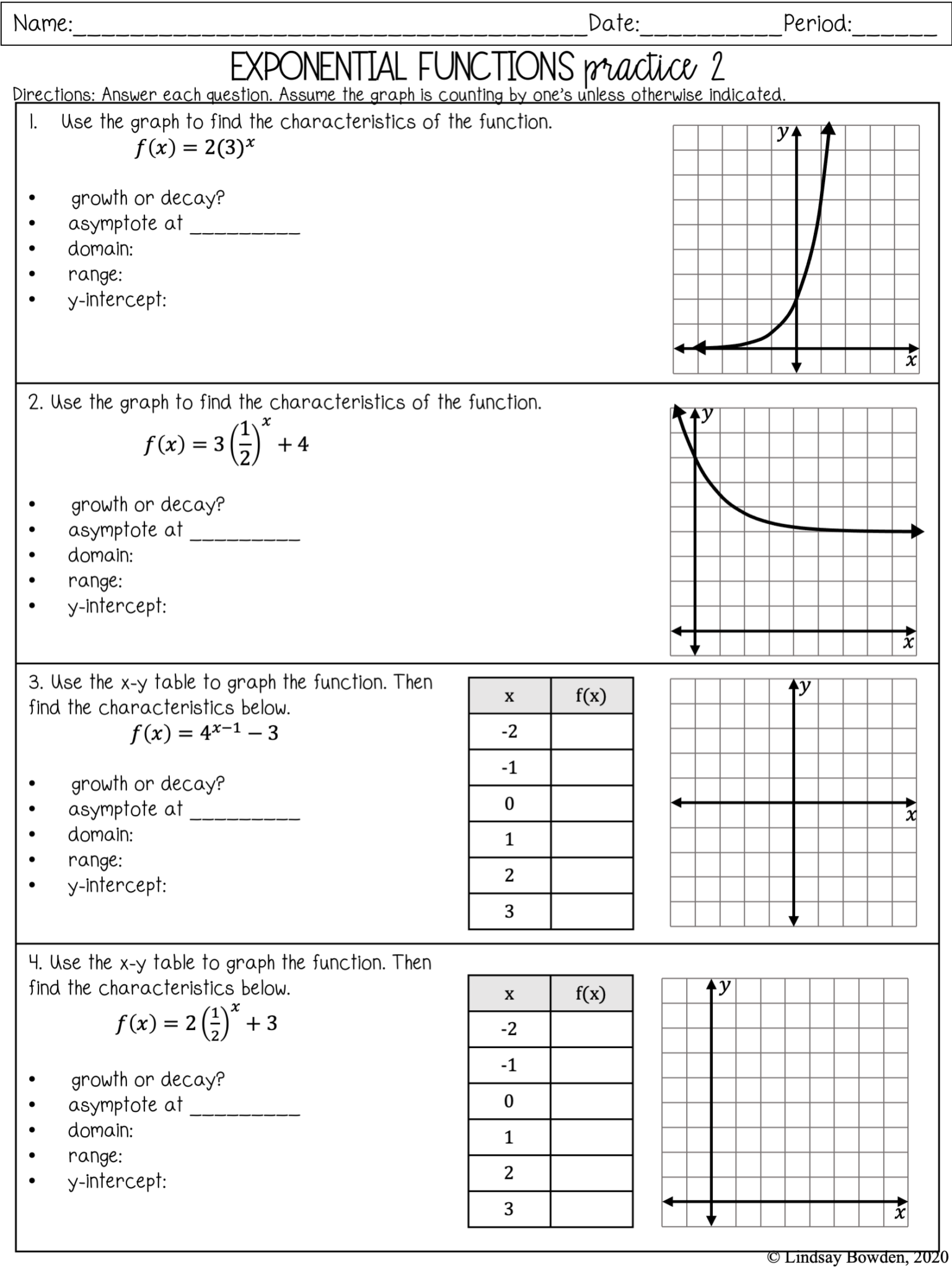
Graph Analysis

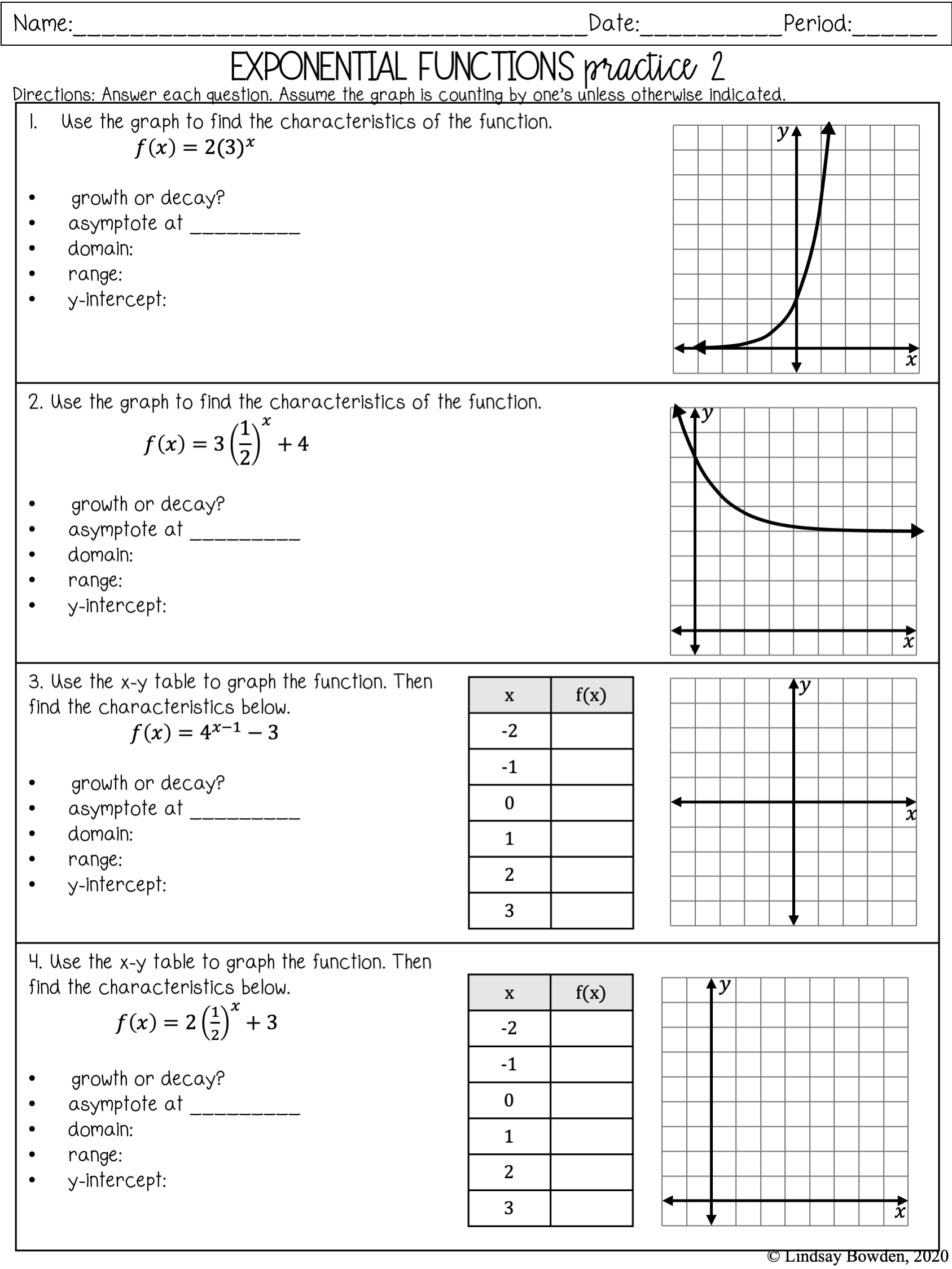
4. Graph Sketching

Sketch the graph of f(x) = 2^x:

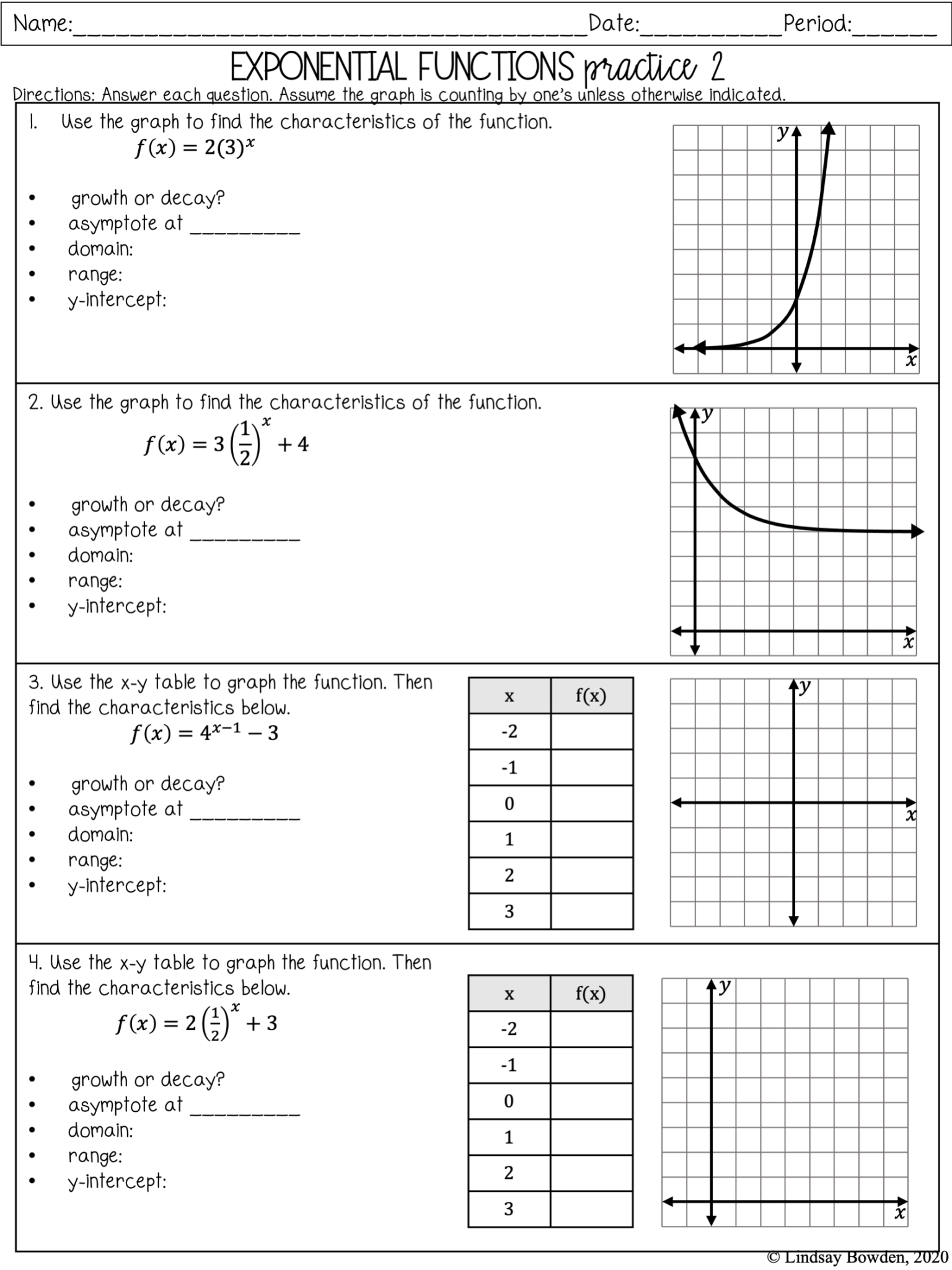
Plotting these points and joining them with a smooth curve, the graph shows exponential growth.

Real-World Applications

5. Investment Growth

If you invest $1000 at an annual interest rate of 5%, compounded annually, how much will you have after 10 years?

Answer: Use the compound interest formula A = P(1 + r/n)^nt, where:

• P = 1000 (Principal amount)
• r = 0.05 (Annual interest rate)
• n = 1 (Compounded annually)
• t = 10 years

Calculating:

A = 1000 * (1 + 0.05/1)¹⁰ ≈ $1628.89

🔍 Note: In real-world scenarios, consider inflation to get a more accurate future value.

FAQ

What are common mistakes when solving exponential function problems?

+

Common mistakes include:

• Confusing the base of the function with the exponent.
• Not recognizing that the base b must be positive and different from 1.
• Misinterpreting transformations (shifting, stretching, compressing) of the function's graph.

Why do we use different bases in exponential functions?

+

Different bases model different rates of growth or decay:

• Bases greater than 1 (b > 1) model exponential growth, like population growth or investment growth.
• Bases less than 1 (0 < b < 1) model exponential decay, like radioactive decay or depreciation.

How do I solve exponential equations?

+

To solve exponential equations:

• Set the exponents equal if the bases are the same.
• Take the logarithm of both sides if the bases are different, then use log properties to solve for the variable.

The exploration of exponential functions through these worksheet answers demonstrates not only their mathematical beauty but also their practical relevance. By understanding their basic properties, how they are transformed, and their real-world applications, students can gain a deeper appreciation for these functions. Whether it’s modeling population dynamics, calculating investment returns, or understanding the decay of radioactive materials, exponential functions provide us with a powerful tool to interpret and predict changes over time. This journey through evaluation techniques ensures that students are equipped with the knowledge to tackle any exponential problem with confidence and accuracy.