5 Essential Steps for Mastering Equivalent Fractions
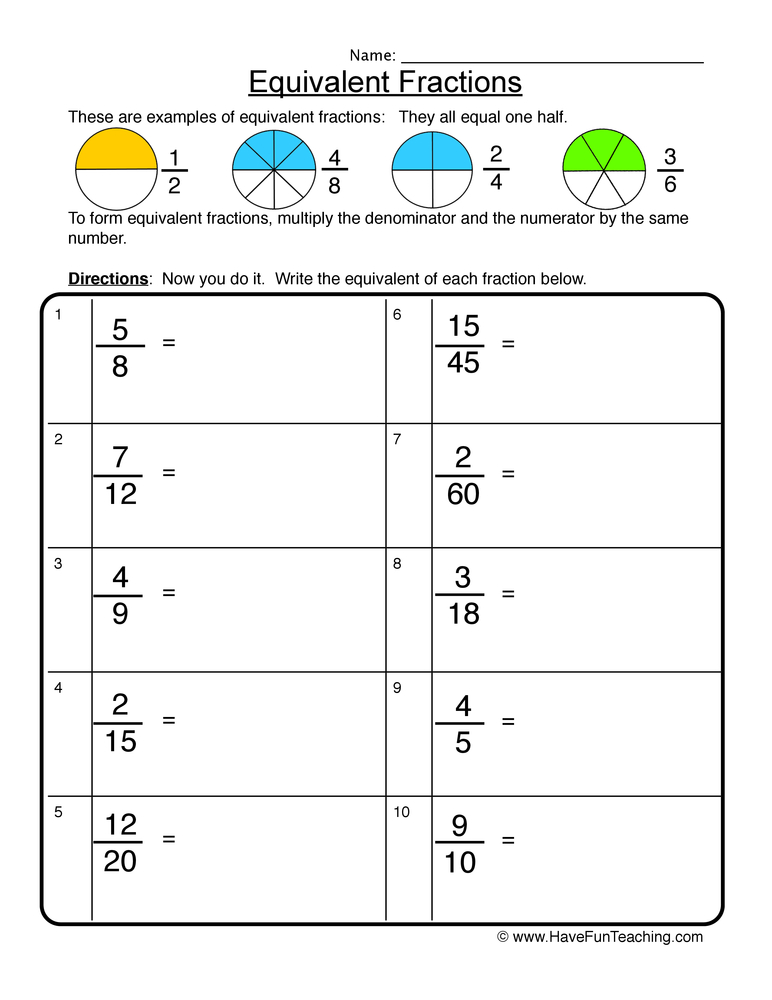
Understanding equivalent fractions is fundamental to mastering math at various levels. Whether you're helping a child with homework or refreshing your own knowledge, knowing how to handle equivalent fractions can significantly enhance your numerical literacy. Here are five essential steps to not only understand but also master the concept of equivalent fractions.
1. Grasping the Basics of Fractions

Before diving into equivalent fractions, it’s crucial to comprehend what a fraction is. A fraction represents a part of a whole, with two parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, which shows how many parts make up the whole.
When you express a part of an object or a group, you’re essentially creating a fraction. For instance, if you have a pizza and slice it into 4 equal pieces and take one of those slices, you have 1⁄4 of the pizza.
2. Understanding the Concept of Equivalence
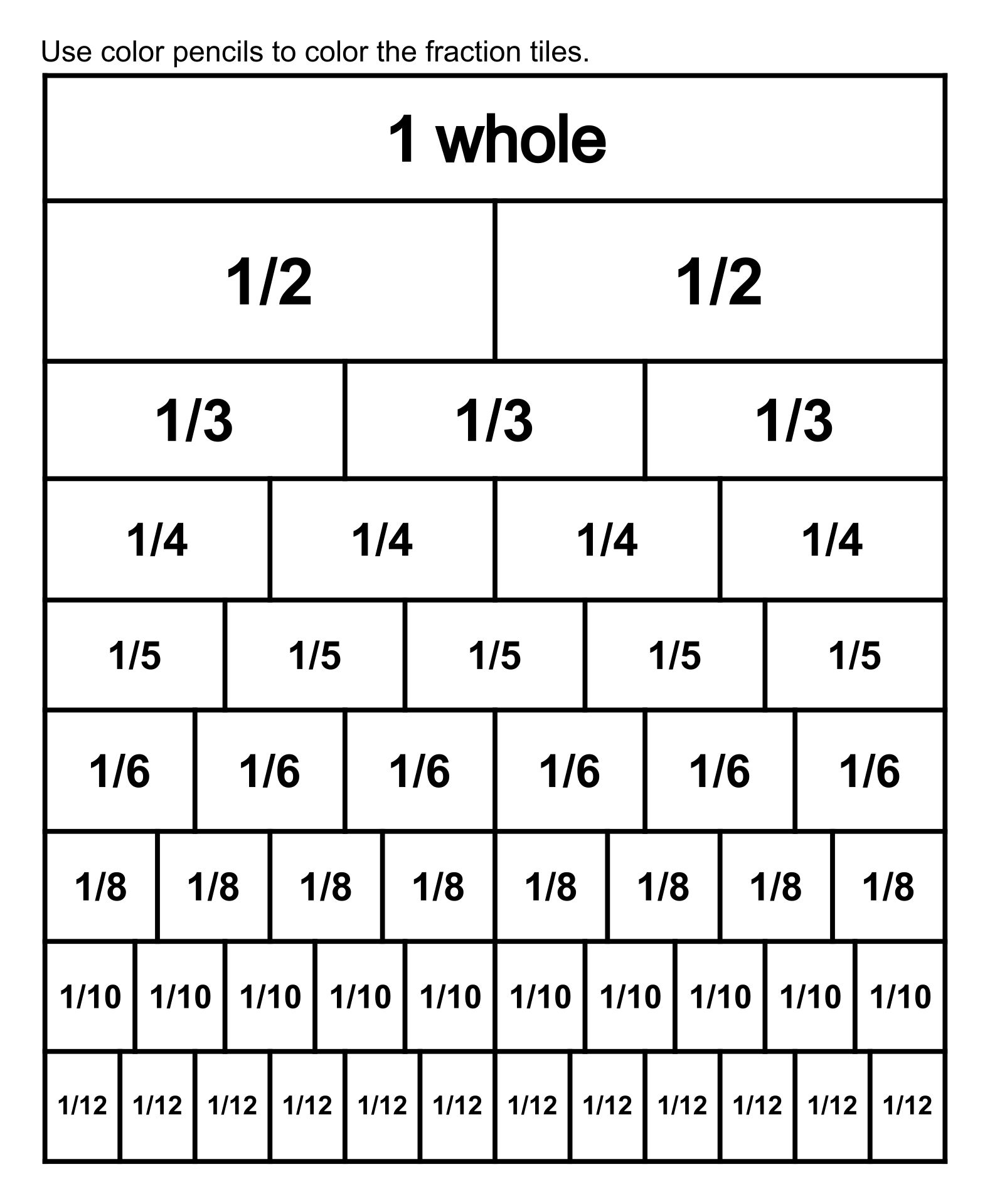
Two fractions are equivalent if they represent the same quantity, even though their numerical forms might differ. This equivalence arises from:
- Multiplying or dividing both the numerator and the denominator by the same number (not zero).
- Simplifying a fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD).
Consider the fractions 1⁄2, 2⁄4, and 4⁄8. These are all equivalent because they represent the same proportion of a whole, just expressed with different numbers.
3. Finding Equivalent Fractions through Multiplication

One straightforward method to find equivalent fractions involves multiplying both the numerator and the denominator by the same number. For example:
If you start with 3⁄4 and multiply both by 3:
| Numerator | Denominator |
| 3 × 3 = 9 | 4 × 3 = 12 |
| 9⁄12 is equivalent to 3⁄4 | |

4. Simplifying Fractions to Find Equivalents

Simplifying fractions by finding the greatest common divisor (GCD) is another approach to establish equivalence:
Take 8⁄12 for instance:
- The GCD of 8 and 12 is 4.
- Dividing both numbers by 4 gives:
- 8⁄4 = 2 and 12⁄4 = 3, resulting in the equivalent fraction 2⁄3.
Remember, you can only simplify a fraction by factors shared by both the numerator and the denominator.
5. Practicing with Real-Life Examples

Practical application helps solidify the concept of equivalent fractions. Here are some ways to practice:
- Recipes: Adjusting recipe quantities (doubling or halving) uses equivalent fractions.
- Measurements: Converting measurements from one unit to another, like inches to feet, involves equivalent fractions.
- Board Games: Dividing points or pieces among players can be done using equivalent fractions to ensure fairness.
⚠️ Note: Always ensure that when simplifying or making equivalent fractions, you’re consistent in your approach, as incorrect operations can lead to incorrect outcomes.
Mastering equivalent fractions isn't just about academic success; it's about building a foundation for logical thinking and problem-solving. By understanding the nature of fractions, identifying when they are equivalent, and practicing these skills in real-life scenarios, you'll find mathematics becoming more intuitive and manageable. This knowledge will serve as a cornerstone for more complex topics in mathematics, helping you navigate through algebra, geometry, and beyond with greater ease.
Why do we need to know about equivalent fractions?
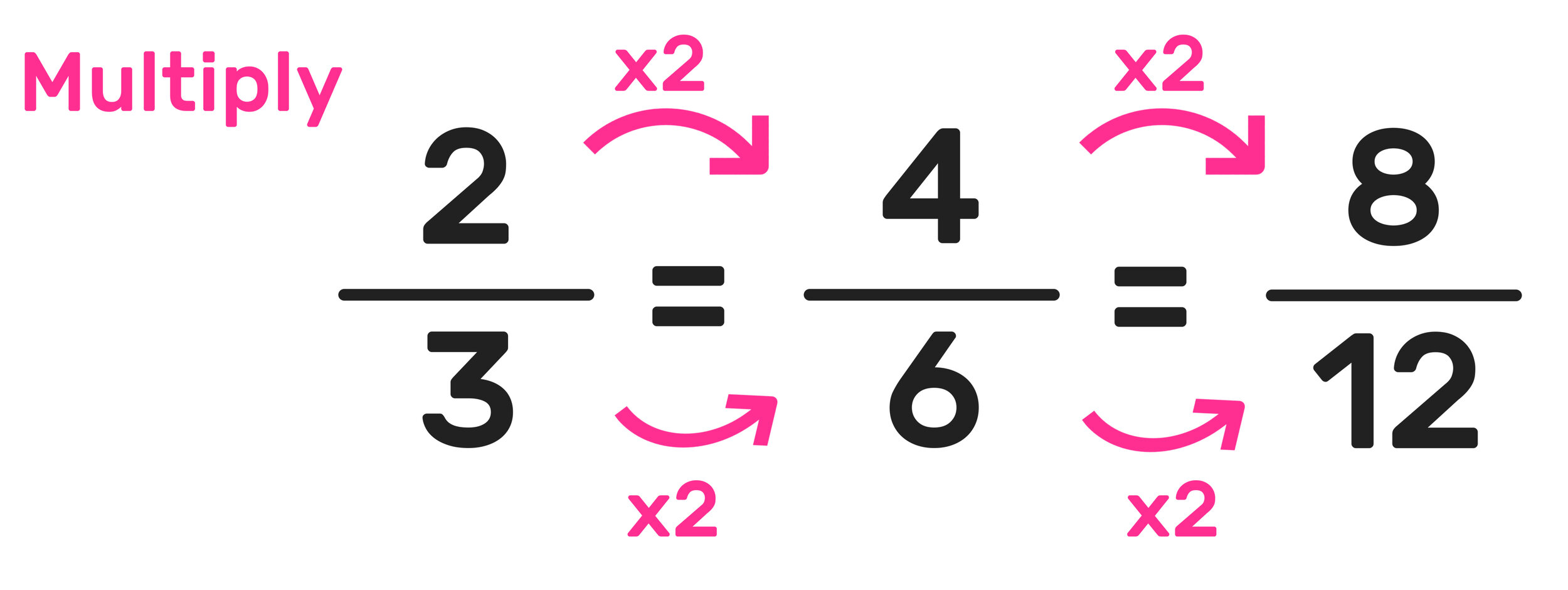
+
Equivalent fractions help us understand that different numerical representations can denote the same value, which is essential for comparing quantities, solving equations, and understanding ratios and proportions.
Can all fractions be simplified?

+
Yes, every fraction can be simplified as long as both the numerator and the denominator are divisible by a common factor greater than 1.
How do I know if two fractions are equivalent?

+
Two fractions are equivalent if when reduced to their simplest form, they share the same value. You can also cross-multiply the numerators and denominators to see if they yield the same result.



