End Behavior Worksheet: Mastering Calculus Limits

Exploring limits is a fundamental concept in calculus, guiding us to understand how functions behave as they approach specific points. One crucial aspect of limits is understanding end behavior, which involves analyzing how functions act when the variable approaches infinity or negative infinity. In this detailed guide, we'll delve deep into the end behavior of various types of functions to better comprehend their behavior as x heads towards extremes.
Understanding End Behavior

End behavior refers to the value a function approaches as x moves towards positive or negative infinity. This behavior provides insight into the function’s growth, decay, or asymptotic tendencies. Here are some key points to understand:
- Polynomial Functions: For functions like f(x) = x^n, the degree of the polynomial dictates its end behavior.
- Rational Functions: The end behavior here depends on the degrees of the numerator and denominator.
- Exponential Functions: Functions of the form e^x or a^x typically approach infinity or zero as x goes to infinity or negative infinity.
Let's break down how to analyze these behaviors:
End Behavior of Polynomials

Polynomials, especially those with only one term (monomials), are straightforward:
- If n is even, f(x) = x^n grows without bound in both directions.
- If n is odd, f(x) = x^n approaches positive infinity as x goes to positive infinity, and negative infinity as x goes to negative infinity.
| Function | End Behavior as x → +∞ | End Behavior as x → -∞ |
|---|---|---|
| f(x) = x^2 | ∞ | ∞ |
| f(x) = x^3 | ∞ | -∞ |
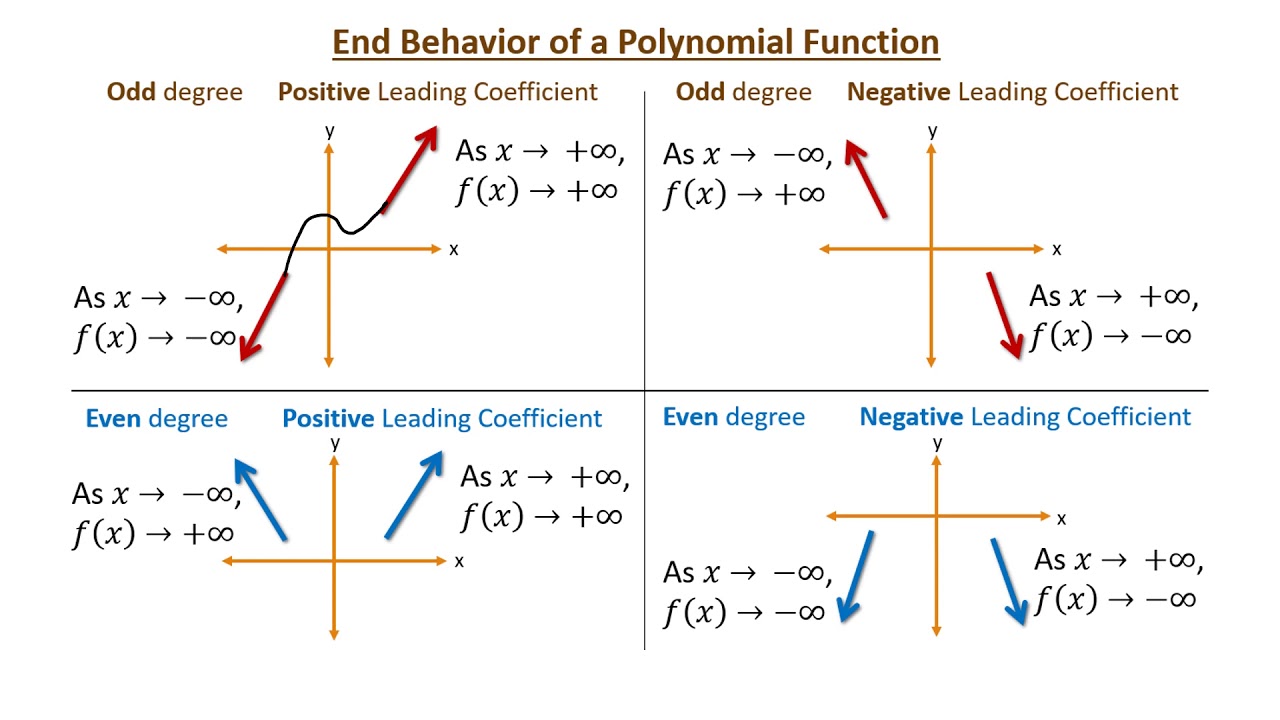
📝 Note: For higher degree polynomials, the leading term predominantly dictates end behavior.
End Behavior of Rational Functions

For rational functions of the form f(x) = P(x)/Q(x):
- If degree P(x) < deg Q(x), the function approaches 0.
- If degree P(x) > deg Q(x), the function’s behavior is similar to a polynomial.
- If degrees are equal, the end behavior is defined by the quotient of the leading coefficients.
End Behavior of Exponential Functions

Exponential functions display unique behaviors:
- If a > 1, f(x) = a^x goes to infinity as x goes to positive infinity.
- If 0 < a < 1, f(x) = a^x approaches zero as x goes to positive infinity, and it grows towards infinity as x goes to negative infinity.
📝 Note: The behavior of e^x is particularly important in calculus due to its derivative and integral properties.
Practical Examples

Let’s examine a few functions to illustrate end behavior:
- f(x) = 2x^5 - 3x^2 + 1: Since the leading term is 2x^5, which has an odd degree and positive coefficient, the function approaches infinity as x goes to infinity.
- f(x) = (3x^4 + 2x^3)/(x^5 + 1): Here, the degree of the numerator (4) is less than the denominator (5), hence the function approaches 0 as x goes to both positive and negative infinity.
- f(x) = e^x: Exponential growth to positive infinity.
Common Misconceptions

Here are some areas where students often get confused:
- Confusion with Leading Coefficients: The leading coefficient determines whether a function approaches positive or negative infinity, not its exact growth rate.
- Overlooking the Dominant Term: In polynomial functions, focusing on the term with the highest power is crucial.
- Behavior at Infinity: Functions with even degree polynomial numerator or denominator often approach asymptotes, not infinity.
In conclusion, understanding end behavior is vital for mastering calculus limits. By analyzing how different functions behave as x approaches infinity or negative infinity, we can predict the long-term behavior of graphs, solve equations involving limits, and comprehend real-world applications of calculus. This knowledge also forms the backbone for understanding concepts like improper integrals, the behavior of derivatives at infinity, and the use of limits in sequence analysis.
What is end behavior in calculus?

+
End behavior describes how a function’s value changes as the input variable approaches either positive or negative infinity. It gives us insight into the function’s overall behavior at the extremes of its domain.
Why is understanding end behavior important?

+
Understanding end behavior helps in sketching the graph of a function, solving limits, identifying asymptotes, and analyzing the long-term behavior of real-world mathematical models.
How do you determine the end behavior of a polynomial function?

+
The end behavior of a polynomial is mainly determined by its leading term. If the degree (n) is even, the function will approach either positive or negative infinity in both directions. If n is odd, the function will approach opposite infinities depending on the sign of the leading coefficient.
Can a function have different end behaviors for positive and negative infinity?

+
Yes, especially in the case of odd-degree polynomials and rational functions with numerator and denominator having different degrees. The function can approach positive infinity on one side and negative infinity on the other.
What about the end behavior of exponential functions?

+
Exponential functions with a base greater than 1 grow to positive infinity as x approaches positive infinity, and those with a base between 0 and 1 approach zero as x goes to positive infinity.



