Domain and Range Worksheet Answers Explained

Understanding the concepts of domain and range is fundamental in mathematics, particularly in the study of functions. These concepts are not only crucial for grasping how functions behave but also for solving various problems in calculus, algebra, and beyond. This comprehensive guide will explore domain and range in depth, offering detailed explanations and answers to common worksheets to solidify your understanding.
What is Domain and Range?

Domain: The domain of a function is the complete set of possible values of the independent variable or set of input values for which the function is defined. Think of it as the universe from which you can pick your x-values when dealing with functions.
Range: On the other hand, the range refers to all possible values that the function can take, or all the outputs (y-values) that the function can produce when you apply the function to every element of the domain.
To visualize this:
- The domain is the set of all permissible x-values for a function.
- The range is the set of all corresponding y-values that result from these x-values.
Determining Domain and Range of Functions

1. Polynomial Functions

Polynomial functions, such as (f(x) = x^2), have:
- Domain: All real numbers ( (-\infty, \infty) ) because you can square any real number.
- Range: Also all real numbers for odd-degree polynomials, but for even-degree polynomials like (x^2), the range is ([0, \infty)), as (x^2) cannot yield negative numbers.
⚠️ Note: Watch out for restrictions due to undefined operations like division by zero or taking even roots of negative numbers.
2. Rational Functions

Consider a function like (f(x) = \frac{1}{x})
- Domain: (x \neq 0). The function is undefined when the denominator is zero.
- Range: All real numbers except zero. As (x) approaches zero from the left, (f(x)) approaches negative infinity, and from the right, it approaches positive infinity.
3. Functions with Square Roots or Logs

Take (f(x) = \sqrt{x}) for example:
- Domain: ([0, \infty)). You can’t take the square root of a negative number in the real number system.
- Range: ([0, \infty)). A square root of a real number will always be non-negative.
Worksheet Answers

Let's delve into some common worksheet problems to understand how to find the domain and range:
Example 1: f(x) = 3x - 5

- Domain: Since 3x - 5 is a linear function, it's defined for all real numbers. Thus, the domain is (-\infty, \infty) .
- Range: Similarly, the function can take on any real number. The range is also (-\infty, \infty) .
Example 2: f(x) = \frac{x-1}{x+2}

- Domain: Exclude x = -2 from the domain since the denominator can't be zero. Domain: (-\infty, -2) \cup (-2, \infty) .
- Range: There's a vertical asymptote at x = -2. Also, as x \rightarrow -2 from the left, f(x) \rightarrow -\infty, and from the right, f(x) \rightarrow \infty. Hence, the range is (-\infty, \infty) .
| Function | Domain | Range |
|---|---|---|
| f(x) = \sqrt{16 - x^2} | [-4, 4] | [0, 4] |
| f(x) = \frac{1}{x^2 - 4} | All real except ±2 | All real except 0 |

🌟 Note: Always consider the continuity of functions when finding their domain and range.
Strategies for Finding Domain and Range

Identifying Restrictions

There are several restrictions to watch out for:
- Division by Zero: Avoid any (x)-value that makes the denominator zero in a rational function.
- Negative Square Roots: For functions involving even roots, the argument must be non-negative.
- Logarithms: The argument of a log function must be positive.
Graphical Analysis
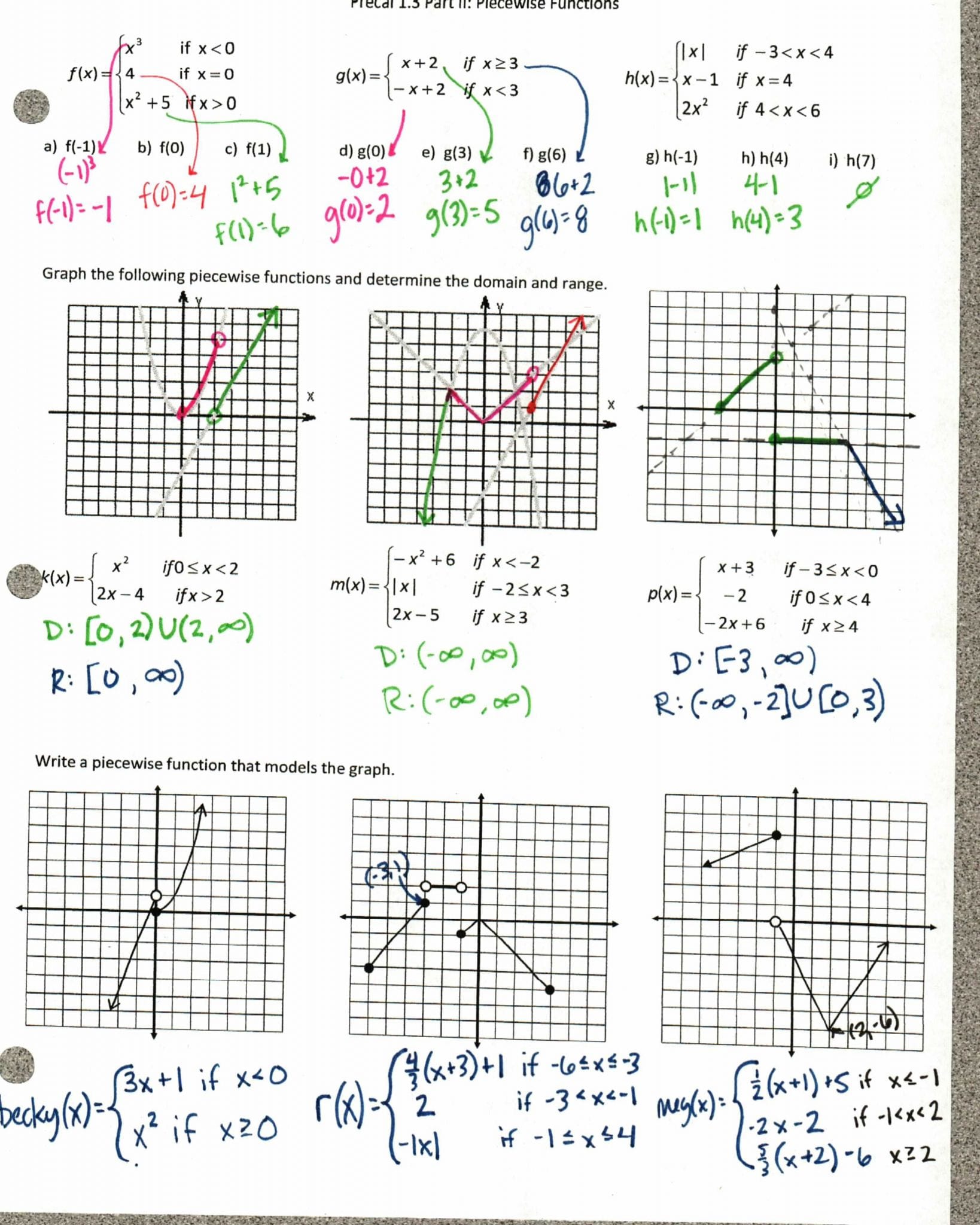
Graphing a function can often reveal:
- Vertical Asymptotes or Holes which restrict the domain.
- Horizontal Asymptotes or Finite Limits which can help with the range.
- Turning Points or Maxima/Minima which are critical for understanding range boundaries.
Analytical Methods

Analyzing the function mathematically can:
- Help with domain by solving inequalities for undefined regions.
- Reveal potential range limitations through critical points or asymptotes.
Advanced Considerations

Functional Composition
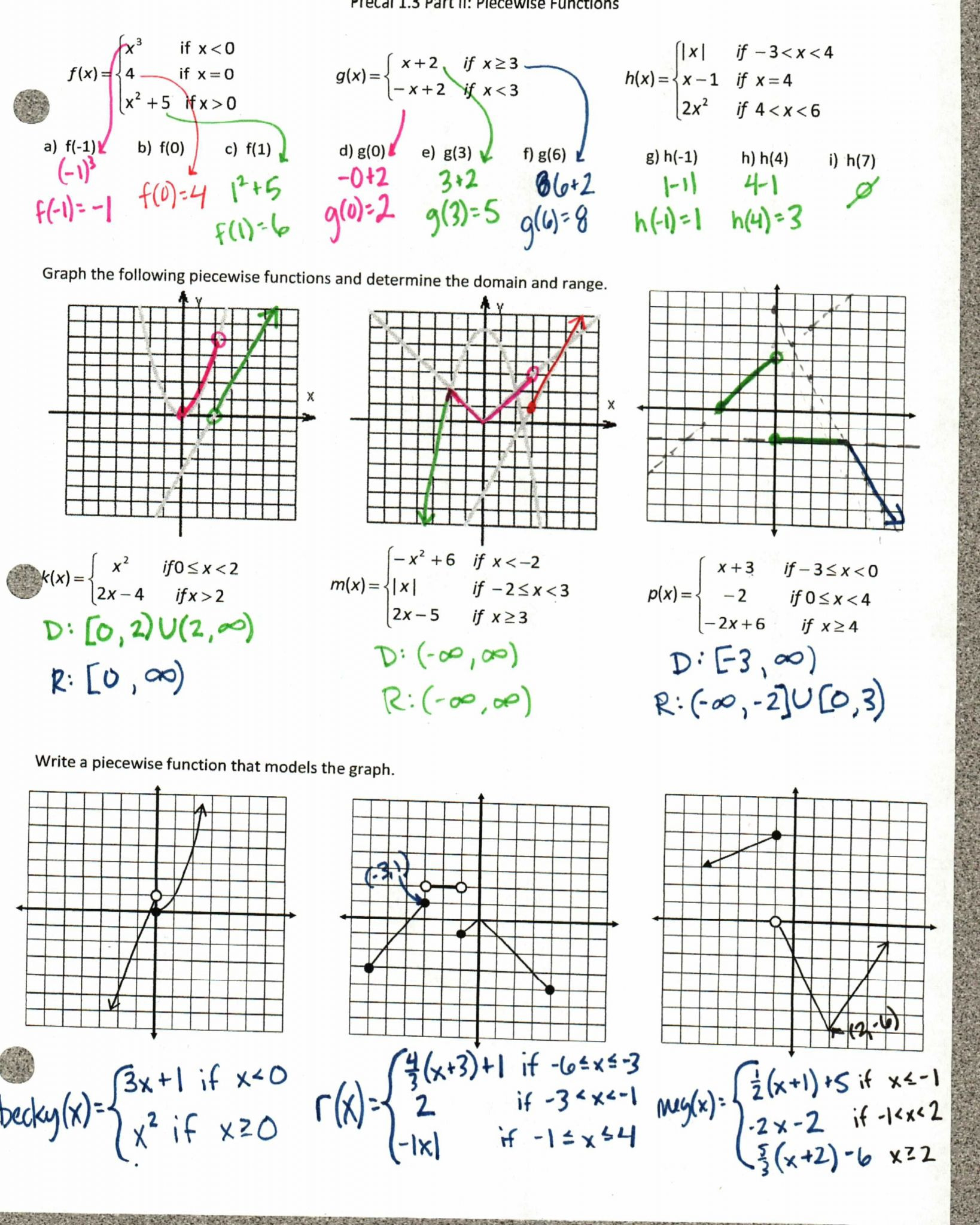
When dealing with composite functions (g(f(x))), the domain is influenced by both (f) and (g):
- The output of (f) must be within the domain of (g).
- The range of (g(f(x))) will also depend on how (g) operates on the outputs of (f).
Transformations

Shifts, stretches, or reflections of a function:
- Change the domain or range by altering the function’s behavior.
- Horizontal shifts affect the domain, while vertical shifts affect the range.
👀 Note: Multiple or nested transformations can significantly alter domain and range calculations, requiring a methodical approach.
Wrapping Up

Domain and range are foundational concepts that help us understand functions’ behavior, solve equations, and analyze the extent of their applicability. This guide has walked you through the basic definitions, methods to determine domain and range, practical examples from worksheets, and more nuanced considerations for advanced scenarios. By mastering these concepts, you’ll enhance your ability to comprehend and manipulate functions in various mathematical contexts, ensuring a solid foundation for further studies or problem-solving.
How do you find the domain of a function with a square root?
+Set the expression inside the square root greater than or equal to zero and solve for x to find the domain. Ensure the expression inside the square root is always non-negative.
What does a vertical asymptote indicate in terms of a function’s domain and range?
+A vertical asymptote indicates that the function approaches either positive or negative infinity at the point where the asymptote exists, making the function undefined at that point. This restricts the domain but does not directly affect the range.
How does the range change if the function undergoes a vertical shift?
+A vertical shift moves the function up or down by a constant value, directly affecting the range. If (f(x)) is shifted up by (k), the range also shifts by (k).


