5 Ways to Divide Fractions by Whole Numbers Easily

When you encounter the task of dividing fractions by whole numbers, it might initially seem daunting. However, with a few simple strategies and conceptual understanding, this process can become remarkably straightforward. Here, we will explore five effective methods to divide fractions by whole numbers, ensuring clarity and ease in your mathematical journey.
Understanding the Basics

Before we dive into the methods, let's solidify the fundamentals:
- A fraction represents part of a whole, where the numerator indicates the number of parts taken, and the denominator indicates the total number of parts.
- Dividing by a whole number can be thought of as finding how many times that number fits into the fraction or breaking it into smaller, equal pieces.

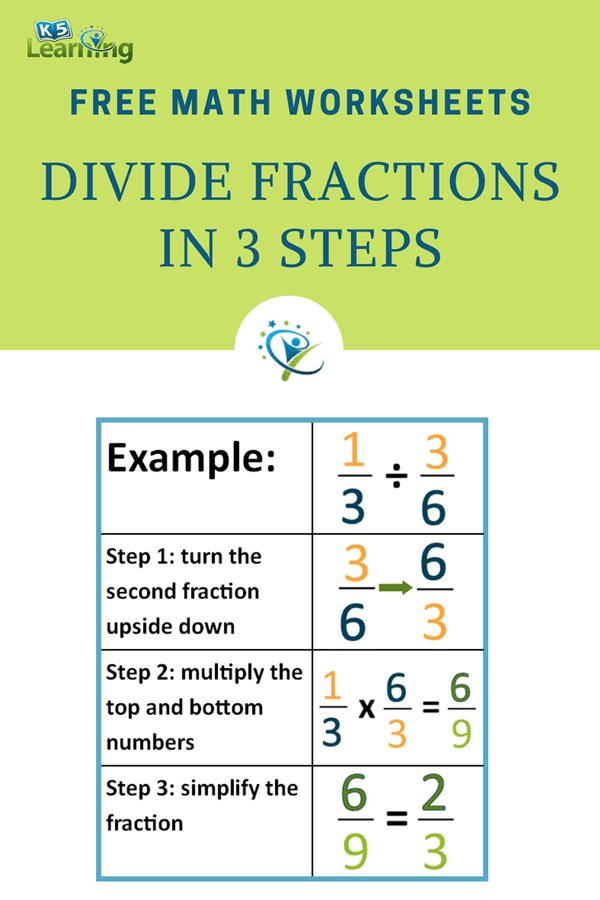
Method 1: Multiply by the Reciprocal

The most common and perhaps the easiest method for dividing fractions is to multiply by the reciprocal of the whole number. Here's how you do it:
- Convert the whole number into a fraction by placing it over 1.
- Find the reciprocal of the new fraction by swapping its numerator and denominator.
- Now, multiply your original fraction by this reciprocal:
3/4 ÷ 5 = 3/4 * 1/5 = 3/20
🔎 Note: Remember, when you see a division sign in fractions, think of it as multiplication by the reciprocal.
Method 2: Use a Number Line for Visual Learners

For visual learners or those who grasp concepts better with illustrations:
- Draw a number line and mark off the whole number segments.
- Divide each segment according to the fraction's denominator to represent the parts.
- Now, divide these segments by the whole number to see how many groups you get. Here's an example:
1/2 ÷ 4 on a number line shows that 4 fits into 1/2 a total of 1/8 times.

Method 3: The "Parts per Whole" Approach

This method involves understanding fractions in terms of parts per whole:
- If you have 1/3 and you divide it by 2, you essentially divide the part into 2 equal sections, each representing 1/6 of the whole.
- You can see this visually or solve it mathematically:
1/3 ÷ 2 = 1/3 × 1/2 = 1/6
Method 4: Employing Bar Models

Bar models provide a visual aid for mathematical operations:
- Draw a bar representing 1 whole and divide it into equal segments based on the fraction's denominator.
- Divide each of these segments into parts equal to the whole number you're dividing by:
For 3/4 ÷ 3, draw 4 segments, then divide each into 3 parts, giving you 1/4 of each segment or 1/12 of the whole.

Method 5: Utilizing the "When-Then" Technique

Think of the problem in terms of 'when-then':
- When you have 1/5 of a whole and you divide it into 4 equal pieces, then each piece is 1/20 of the whole.
- This method encourages conceptual thinking:
1/5 ÷ 4 = 1/5 × 1/4 = 1/20
As we conclude our exploration, remember that the essence of dividing fractions by whole numbers lies in understanding the concept of division. Whether you use multiplication by the reciprocal, visual aids like number lines or bar models, or conceptual techniques like "when-then" or "parts per whole," each method simplifies the process by breaking it down into relatable, understandable steps. Embrace these techniques, practice them, and they will soon become second nature, making you adept at handling fractions in various mathematical contexts.
What does it mean to divide a fraction by a whole number?

+
Dividing a fraction by a whole number means finding how many times the whole number can fit into the fraction or how many equal parts you can break the fraction into.
Can I use the same methods for dividing whole numbers by fractions?

+
The methods for dividing fractions can generally be adapted for dividing whole numbers by fractions, with some adjustments. For example, multiplying by the reciprocal works both ways.
What if the whole number is larger than the denominator of the fraction?
+
When the whole number is larger, the result will be a fraction smaller than 1. You’ll still proceed with the methods, which often leads to simplifying the result.
Are there any common mistakes to avoid when dividing fractions by whole numbers?

+
Common mistakes include not converting the whole number to a fraction, forgetting to multiply by the reciprocal, and misinterpreting the division sign’s meaning in fractions.
How do I verify my answers when dividing fractions by whole numbers?

+
To verify, multiply your result by the whole number to check if it equals the original fraction. This method of checking works due to the inverse relationship between division and multiplication.