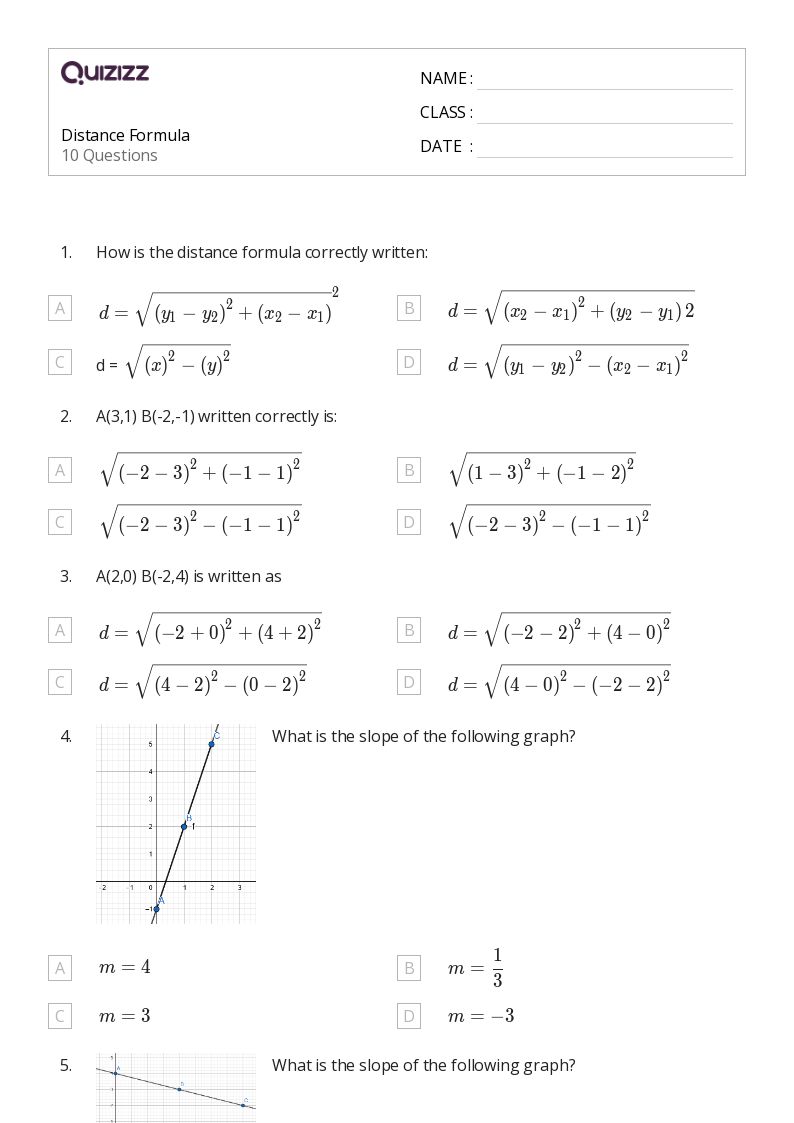
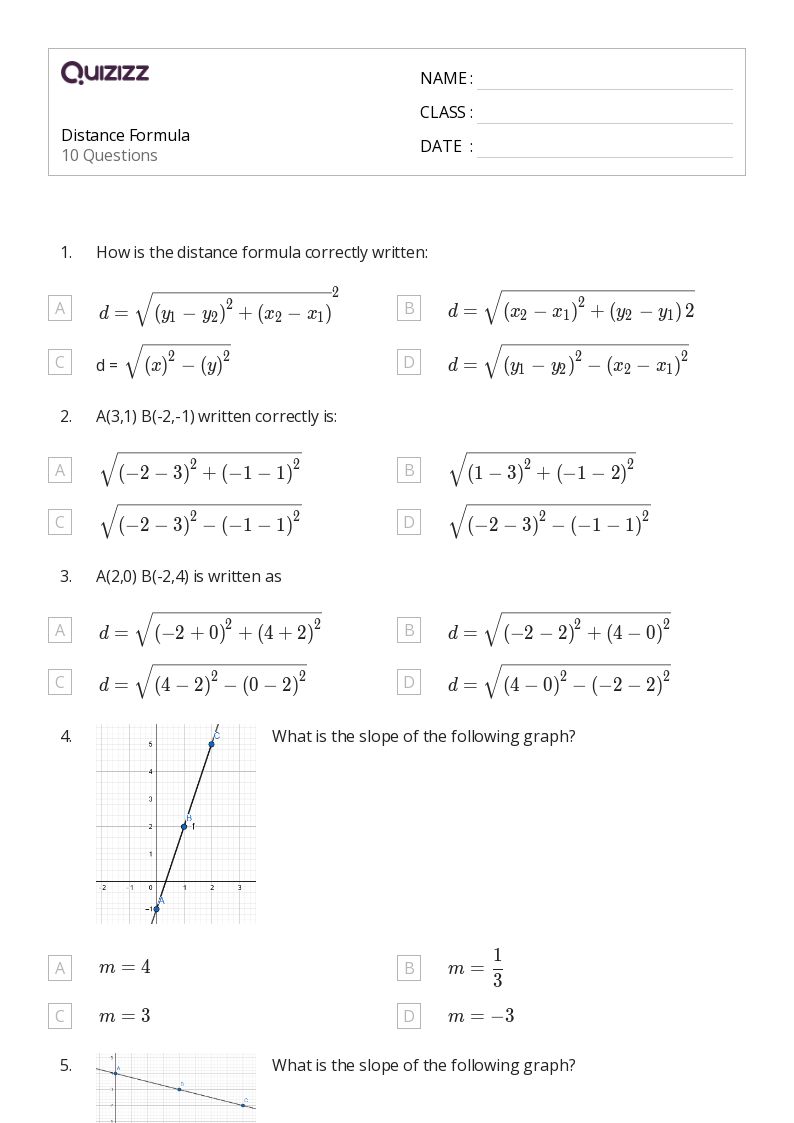
Distance Formula Worksheet 2 Answer Key Revealed

When studying coordinate geometry, one of the fundamental concepts you encounter is the distance formula. This mathematical tool allows you to calculate the straight-line distance between two points in a plane. Today, we're going to delve into the second worksheet on the distance formula, unraveling the answer key and giving you insights on how to approach these problems effectively. Whether you're a student aiming for a better understanding or a teacher looking for explanations to help your students, this detailed exploration will prove invaluable.
Understanding the Distance Formula
Before jumping into the worksheet answers, it's crucial to understand the formula itself:
\[ \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- The formula calculates the distance between two points (x_1, y_1) and (x_2, y_2).
- Subtract the x-coordinates and the y-coordinates, square both differences, add the squares, and then take the square root of the result.
The Worksheet Answers
Let's go through each problem in the Distance Formula Worksheet 2 and its solutions:
Problem 1

Find the distance between the points (3, 4) and (7, 10).
The answer:
\[ \text{Distance} = \sqrt{(7 - 3)^2 + (10 - 4)^2} = \sqrt{4^2 + 6^2} = \sqrt{16 + 36} = \sqrt{52} \approx 7.21 \]
Problem 2

Determine the distance from (-2, -1) to (4, 5).
The answer:
\[ \text{Distance} = \sqrt{(4 - (-2))^2 + (5 - (-1))^2} = \sqrt{(4 + 2)^2 + (5 + 1)^2} = \sqrt{6^2 + 6^2} = \sqrt{36 + 36} = \sqrt{72} \approx 8.49 \]
Problem 3

Find the distance between (-5, 6) and (-2, -3).
The answer:
\[ \text{Distance} = \sqrt{(-2 - (-5))^2 + (-3 - 6)^2} = \sqrt{(-2 + 5)^2 + (-3 - 6)^2} = \sqrt{3^2 + (-9)^2} = \sqrt{9 + 81} = \sqrt{90} \approx 9.49 \]
Problem 4
Calculate the distance between the origin (0, 0) and (6, 8).
The answer:
\[ \text{Distance} = \sqrt{(6 - 0)^2 + (8 - 0)^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \]
📚 Note: Make sure to double-check your arithmetic when squaring the coordinates to avoid calculation errors.
Problem 5

Find the distance between the points (-3, 1) and (4, -5).
The answer:
\[ \text{Distance} = \sqrt{(4 - (-3))^2 + (-5 - 1)^2} = \sqrt{(4 + 3)^2 + (-5 - 1)^2} = \sqrt{7^2 + (-6)^2} = \sqrt{49 + 36} = \sqrt{85} \approx 9.22 \]
Understanding these solutions involves more than just applying the formula; it's about visualizing the line segments and predicting outcomes based on the coordinates' placement in the coordinate plane.
Tips for Solving Distance Formula Problems

- Check Your Coordinates: Always ensure you've correctly identified which coordinate is x_1, y_1 and which is x_2, y_2.
- Simplify Before Squaring: Subtracting and simplifying before squaring can prevent arithmetic errors.
- Practice Regularly: The more you practice, the easier it becomes to recognize patterns and anticipate answers.
This dive into the Distance Formula Worksheet 2 answer key not only provides solutions but also highlights the logical steps involved in applying the formula. Now, when you face similar problems, you'll be equipped with both the knowledge and the confidence to solve them accurately.
As we wrap up our exploration of the Distance Formula Worksheet 2, remember that these mathematical techniques are more than mere abstract exercises. They offer practical applications in fields like engineering, physics, and computer graphics, where calculating distances and spatial relationships is crucial.
Can the distance formula be used in three-dimensional space?

+
Yes, for three-dimensional space, the formula extends to include a z-coordinate, giving ( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}).
What if the distance turns out to be a negative value?
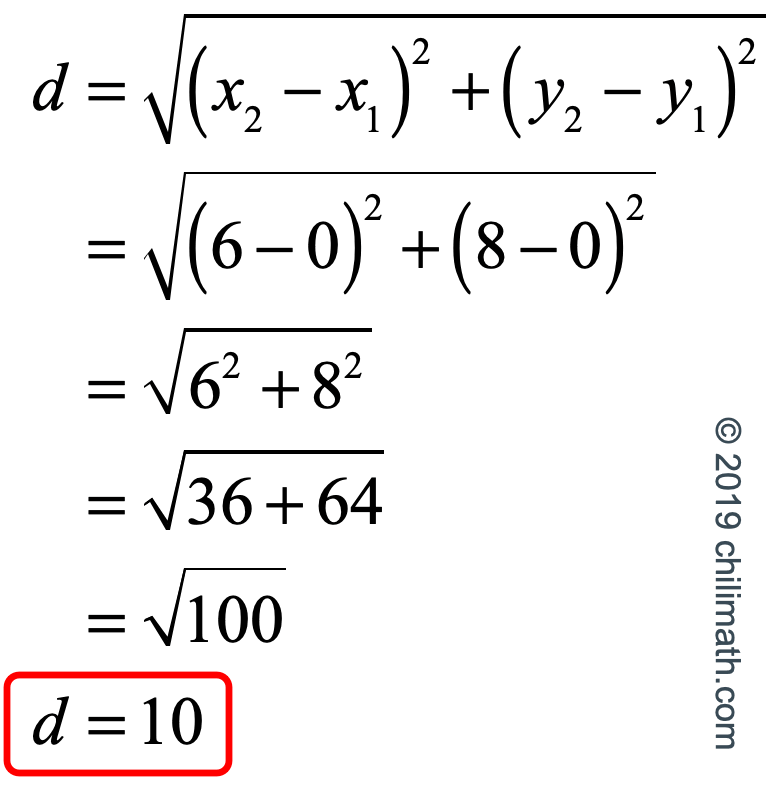
+
Distance cannot be negative; if you get a negative result, it indicates a calculation error.
How does the distance formula relate to the Pythagorean Theorem?

+
The distance formula is essentially an application of the Pythagorean Theorem in a coordinate plane, where the legs of the right triangle are the horizontal and vertical distances between the two points.
Is there an easier way to remember the distance formula?

+
Many find it helpful to remember the Pythagorean Theorem (a^2 + b^2 = c^2) and adjust it for coordinate geometry by using differences in x and y as the sides of the triangle.