5 Essential Tips for Calculating Compound Figure Volumes

Understanding how to calculate the volume of compound figures is crucial for students, engineers, architects, and anyone dealing with complex designs or spatial reasoning. Compound figures, also known as composite shapes, are made by combining two or more basic geometric shapes. Here are five essential tips to ensure you can tackle these calculations with confidence and accuracy:
Identify the Component Shapes


Before you can calculate the volume of a compound figure, you first need to break it down into its constituent geometric shapes. These could include:
- Cubes and cuboids (rectangular prisms)
- Cylinders
- Cones
- Spheres
- Pyramids
- More complex shapes like frustums or truncated pyramids
🔍 Note: If shapes overlap, you'll need to subtract the volume of the overlapping region to avoid overcounting.
Calculate the Volume of Each Shape
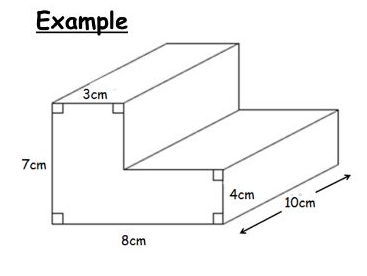
| Shape | Volume Formula |
|---|---|
| Cube | a³ |
| Rectangular Prism | l × w × h |
| Cylinder | πr²h |
| Sphere | (4⁄3)πr³ |
| Cone | (1⁄3)πr²h |
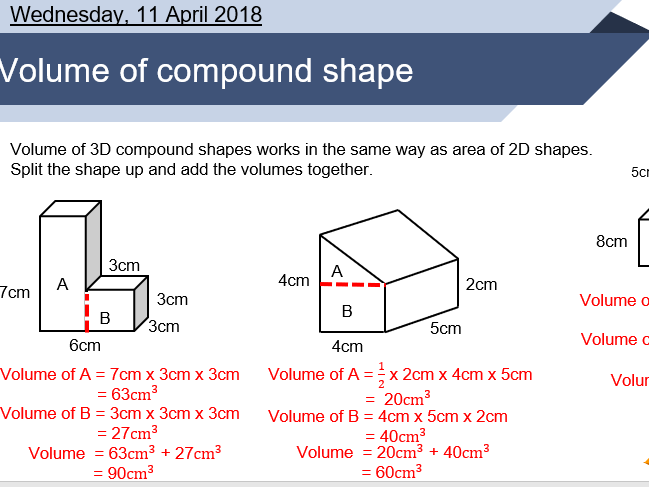
Having identified the shapes, apply the respective volume formulas to compute the volume of each. This step often involves detailed measurements, so accuracy is key.
Consider Intersections and Overlaps

When dealing with compound figures, parts of one shape might intrude into another:
- If shapes intersect or overlap, you must subtract the volume of the overlapping part from the total volume of the individual shapes.
- Use visual aids like diagrams or cross-sections to understand the geometry of the intersection.
Understand Volume of Revolution

For shapes that are derived from rotating a figure around an axis:
- Use the method of volumes of revolution when dealing with cylindrical shapes, cones, or spheres.
- Calculations might require integration, but simpler cases can be managed with standard volume formulas.
Double Check Your Calculations

Errors in measurement or miscalculations can lead to significant discrepancies:
- Ensure units are consistent across all measurements.
- Perform your calculations multiple times or get a peer to verify them.
- If possible, use different methods to estimate the volume as a cross-check.
🔧 Note: Using digital tools or CAD software can provide precise dimensions and volumes, reducing the likelihood of manual errors.
In summary, calculating the volume of compound figures involves breaking the figure down into known shapes, measuring accurately, applying the correct volume formulas, considering intersections or overlaps, and verifying your results. With these techniques in your toolkit, you'll find yourself adept at solving complex volume problems, whether in academic settings, professional environments, or even in everyday life when spatial reasoning is needed.
What if the shape isn’t standard?
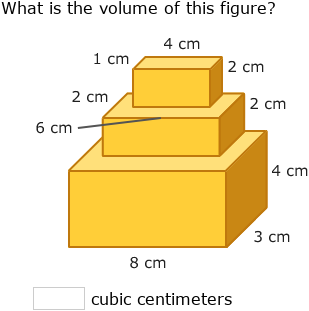
+
If a shape isn’t standard, you can still calculate its volume by breaking it down into parts that can be approximated by standard geometric shapes. Use creative problem-solving, and if necessary, advanced techniques like calculus for exact solutions.
How can I visualize the compound figure?

+
Visual aids like sketches, 3D models, or software such as CAD or even simple apps can help you visualize and break down compound figures into simpler shapes.
Can I estimate the volume if exact measurements are unknown?

+
Yes, you can use approximate measurements or visual estimation techniques, but these should only be used when exact measurements aren’t possible, and you should acknowledge the margin of error in your estimations.