Dilations Practice Worksheet: Master Math Transformations Easily

Understanding Dilations in Mathematics

In the expansive universe of mathematics, dilations stand out as a crucial transformation that affects the size of geometric figures. This article dives deep into what dilations are, how they work, and how they can be mastered through practice. Let's embark on a journey to understand dilations and become adept at this mathematical transformation.
What is a Dilation?

Dilation involves scaling or resizing a figure around a specific point known as the center of dilation. This transformation either enlarges or reduces the size of a shape while keeping its shape intact. Here are the key elements:
- Center of Dilation: The fixed point around which the figure scales.
- Scale Factor: A numerical factor that determines whether the dilation is an enlargement or a reduction.
- Type of Dilation: An enlargement (scale factor > 1) or a reduction (0 < scale factor < 1).

The Process of Dilating

To perform a dilation, follow these steps:
- Identify the center of dilation and the scale factor.
- Draw rays from the center to each vertex of the figure to be dilated.
- Measure the distance from the center to each vertex.
- Multiply these distances by the scale factor.
- Locate the new positions of the vertices along these rays, using the scaled distances.
- Connect the new vertices to form the dilated shape.
🔎 Note: When drawing rays for dilation, ensure they extend beyond the original figure to accommodate the new size.
Real-World Applications of Dilations

Dilations aren’t just theoretical; they have practical uses in:
- Graphic design for resizing images while maintaining proportions.
- Architecture and scale models where dimensions need to be adjusted.
- Medicine for the enlargement of images for detailed examination.
Practicing Dilations

To master dilations, practice is key. Here are some steps to practice:
- Understand the Concept: Review the fundamentals of dilation, focusing on how the scale factor changes the figure’s size.
- Draw it Out: Use graph paper or a geometry software to draw figures and perform dilations, ensuring accuracy with measurements.
- Problem Solving: Work through practice problems that involve different scale factors and different centers of dilation.
The following table provides an overview of the different types of dilations:
| Scale Factor | Type | Effect on Figure |
|---|---|---|
| >1 | Enlargement | Figure grows larger |
| 1 | No Change | Figure remains the same |
| <1 | Reduction | Figure becomes smaller |

📝 Note: Remember that a scale factor of 1 does not change the figure; it's just a special case of dilation.
Common Pitfalls to Avoid
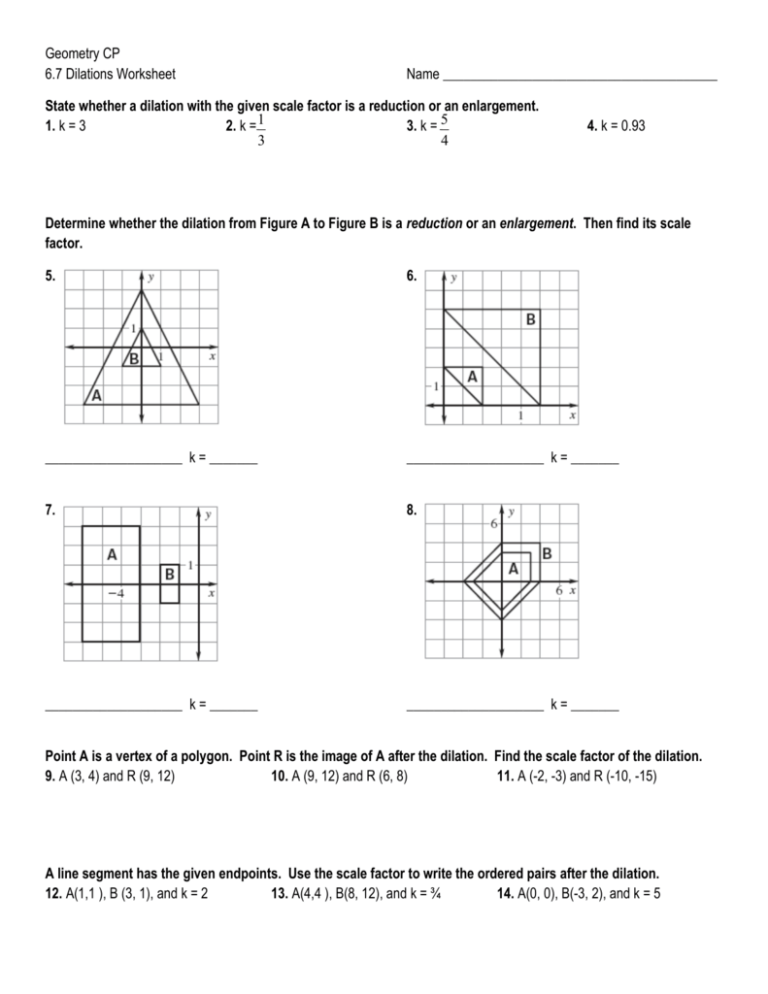
Here are some common mistakes when performing dilations:
- Measurement Errors: Precision in measuring distances from the center of dilation is crucial.
- Incorrect Center: Misplacing the center of dilation leads to skewed results.
- Ignoring Negative Scale Factors: Negative scale factors can reflect and dilate simultaneously.
In mastering dilations, understanding these common errors helps avoid frustration and improves accuracy.
As we near the end of this journey into dilations, it's clear that this transformation is a fundamental tool in both the theoretical understanding and practical application of geometry. By practicing and comprehending the nuances of dilations, students can not only excel in their math assignments but also apply these principles in real-world contexts. Dilations teach us about scale, proportion, and precision, which are all essential in fields like design, architecture, and science.
Can dilations change the shape of a figure?

+
No, dilations do not alter the shape of the figure; they only change its size.
What happens if the scale factor is less than 1?

+
If the scale factor is less than 1, the figure undergoes a reduction, making it smaller.
How can dilations help in graphic design?

+
In graphic design, dilations are used to resize images or elements proportionally, ensuring that the visual integrity and proportions are maintained.