5 Effective Ways to Master Mixed Number Arithmetic

Welcome to an in-depth exploration of mixed number arithmetic! Mastering mixed numbers can greatly enhance your mathematical prowess, offering a solid foundation in fractions, which is crucial for various higher-level calculations and everyday applications. Whether you're a student grappling with schoolwork, a parent helping with homework, or an adult refreshing your math skills, understanding mixed numbers will prove invaluable. This guide will provide you with effective strategies to become proficient in mixed number arithmetic.
Understanding Mixed Numbers

Before we dive into the methods, let’s clarify what mixed numbers are. A mixed number consists of a whole number and a fraction. For example, 2 3⁄4 is a mixed number, where 2 is the whole number and 3⁄4 is the fractional part. Here are the basics:
- A mixed number is always positive, though its fractional part can be positive or negative.
- It’s a combination of a whole number and a proper fraction.
- Mixed numbers can be converted into improper fractions and vice versa.
Method 1: Converting Between Mixed Numbers and Improper Fractions
Understanding the conversion between mixed numbers and improper fractions is a key step in mastering mixed number arithmetic. Here’s how you do it:
Converting Mixed Numbers to Improper Fractions

- Multiply the whole number by the denominator of the fraction.
- Add the numerator of the fraction to the result from step 1.
- The numerator of the improper fraction is this sum. Keep the denominator the same.
Example: Convert 3 1/2 to an improper fraction:
3 x 2 = 6, then 6 + 1 = 7. The improper fraction is 7/2.
Converting Improper Fractions to Mixed Numbers

- Divide the numerator by the denominator. The quotient is the whole number part.
- The remainder becomes the numerator of the fractional part, and the denominator stays the same.
Example: Convert 13/4 to a mixed number:
13 ÷ 4 = 3, remainder 1. The mixed number is 3 1/4.
📌 Note: This conversion is essential for simplifying complex fraction operations.
Method 2: Adding and Subtracting Mixed Numbers

Adding and subtracting mixed numbers can be straightforward if you follow these steps:
Adding Mixed Numbers
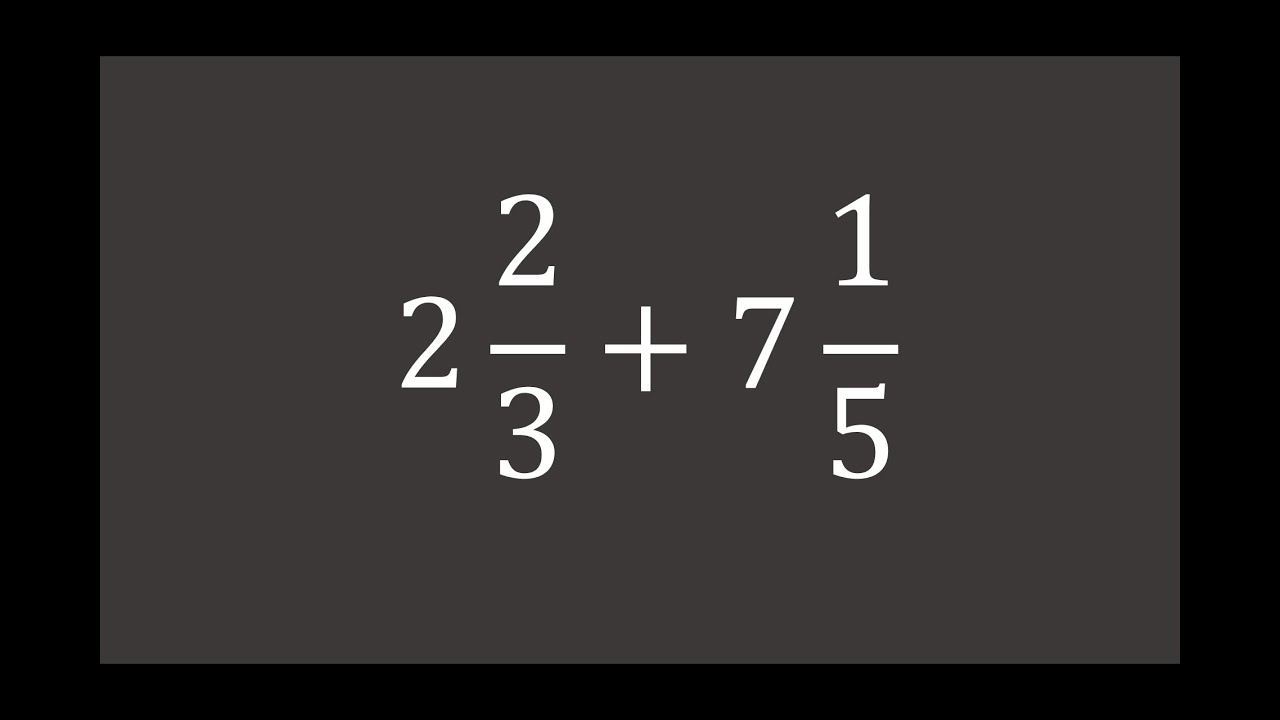
- Add the whole numbers together.
- Add the fractional parts together. If the sum exceeds 1, convert it to a mixed number and carry over the whole number to the whole numbers part.
- Simplify the result if necessary.
Example: Add 2 3/4 + 1 1/2:
Whole numbers: 2 + 1 = 3
Fractions: 3/4 + 1/2 = 3/4 + 2/4 = 5/4 (which is 1 1/4)
Adding the carry-over, the result is 4 1/4.
Subtracting Mixed Numbers

- Subtract the whole numbers together.
- Subtract the fractional parts. If the minuend’s fraction is smaller than the subtrahend’s, you need to borrow 1 from the minuend’s whole number, which will be added to its fractional part to make it larger.
- Simplify the result if necessary.
Example: Subtract 5 1/4 - 3 3/4:
Whole numbers: 5 - 3 = 2
Fractions: 1/4 - 3/4 is not possible without borrowing. So, borrow 1 from 5 (making it 4), and add 1 to the fractional part (1/4 + 4/4 = 5/4):
Now, 5/4 - 3/4 = 2/4 which simplifies to 1/2.
Therefore, the result is 4 1/2.
Method 3: Multiplying and Dividing Mixed Numbers

Multiplication and division with mixed numbers also follow specific procedures:
Multiplying Mixed Numbers

- Convert all mixed numbers to improper fractions.
- Multiply the numerators and then the denominators.
- Convert the resulting improper fraction back to a mixed number if necessary and simplify.
Example: Multiply 3 1/4 by 2 2/3:
Convert to improper fractions: 13/4 x 8/3 = (13 x 8)/(4 x 3) = 104/12.
Convert back: 104/12 = 8 R 8, or 8 2/3.
Dividing Mixed Numbers

- Convert all mixed numbers to improper fractions.
- Use the reciprocal of the divisor.
- Multiply the dividend by the reciprocal of the divisor.
- Convert the result back to a mixed number if necessary and simplify.
Example: Divide 7 1/2 by 2 1/4:
Convert to improper fractions: 15/2 ÷ 9/4.
Now, multiply by the reciprocal: 15/2 x 4/9 = (15 x 4)/(2 x 9) = 60/18.
Simplify: 60/18 = 10/3 or 3 1/3.
Method 4: Simplifying Mixed Numbers

Simplifying mixed numbers involves reducing the fractional part to its simplest form:
- Find the greatest common divisor (GCD) of the numerator and denominator in the fractional part.
- Divide both the numerator and the denominator by the GCD.
Example: Simplify 6 12/18:
The GCD of 12 and 18 is 6:
12 ÷ 6 / 18 ÷ 6 = 2/3. Hence, the simplified form is 6 2/3.
🔍 Note: Simplification is crucial for cleaner arithmetic operations and understanding the magnitude of numbers.
Method 5: Using Models for Visual Understanding

Visual aids can significantly enhance comprehension, particularly for those who are visual or kinesthetic learners. Here are ways to model mixed numbers:
Area Models

Create a grid or use graph paper where each square represents one unit. Illustrate the whole number part with filled squares, and use smaller sections within a square to represent the fractional part.
Number Lines

Draw a number line, marking integer points and divide each segment between two whole numbers to show fractions.
Pie Charts or Circles

Use pie charts or circles, where each whole circle represents one whole number, and fractions of the circle show the fractional part.
These methods not only provide a tangible representation but also make the abstract concept of mixed numbers more tangible and understandable.
Having explored these methods, we come to a natural closing. Mastering mixed numbers involves not just understanding their structure but also how to manipulate them effectively through conversions, operations, simplifications, and visual representations. Each method builds upon a core understanding, enhancing your ability to handle complex arithmetic with ease. Mixed numbers are an integral part of daily life calculations, from dividing recipes to measuring for carpentry projects, ensuring that proficiency in this area serves practical purposes as well as providing a solid foundation for more advanced mathematical concepts.
Why are mixed numbers important?

+
Mixed numbers provide a bridge between whole numbers and fractions, making it easier to express parts of a whole in a more relatable form for everyday applications, like measurements or recipes.
Can mixed numbers be negative?
+The whole number part of a mixed number cannot be negative, but the fractional part can, resulting in a mixed number like -2 3⁄4, which represents subtracting 2 3⁄4 from 0.
What’s the best way to remember the conversion process?
+Practice and visual aids are key. Using visual models or drawing diagrams can help in understanding and remembering how mixed numbers and improper fractions relate to each other.