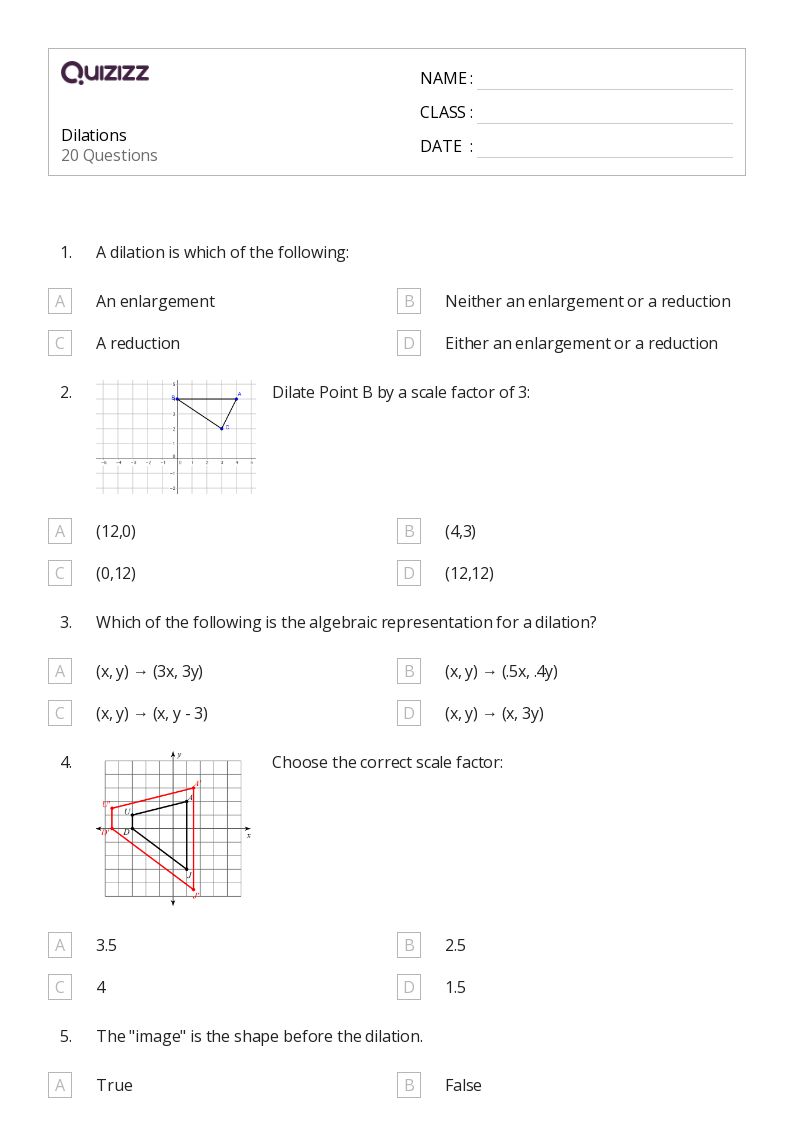
5 Tips for Solving Dilation Worksheets with Answers

Understanding dilation in geometry can be a fascinating yet challenging journey, especially when working through dilation worksheets. This post aims to guide you through five essential tips to simplify this process, ensuring you not only understand the concept but also become proficient in solving these problems efficiently.
Understanding Dilation: A Brief Overview


Before diving into the tips, let’s briefly discuss what dilation means in mathematics. Dilation is a transformation that scales the size of a shape, either expanding or contracting it. This transformation is applied to each point of the original shape by:
- Choosing a center of dilation.
- Using a specific scale factor.
The scale factor determines the extent to which the figure is expanded or contracted:
- When the scale factor is greater than 1, the figure is enlarged.
- When the scale factor is between 0 and 1, the figure is reduced.
Tip 1: Identify the Center of Dilation


The center of dilation is the fixed point through which all other points are scaled. To effectively solve a dilation problem:
- Locate the center of dilation, which can often be labeled directly or found by connecting corresponding points of the original and the dilated figures.
- Understand that the distances of points from the center in the original figure will be multiplied by the scale factor to find the corresponding points in the dilated figure.
Tip 2: Use the Scale Factor Correctly

The scale factor is the key to dilation. Here’s how to use it effectively:
- Determine whether the figure is being expanded or reduced by observing the values provided in the problem.
- Multiply the distance of each point from the center of dilation by this factor to find the new coordinates.
🔍 Note: Remember, when dealing with negative scale factors, the transformation involves reflection as well as dilation.
Tip 3: Employ Coordinate Geometry


If your dilation problem involves coordinates, use these steps:
- Identify the coordinates of the original shape.
- Apply the formula for dilation in a coordinate plane. If the center of dilation is at the origin, the new coordinates (x’, y’) are given by:
- x’ = k * x
- y’ = k * y
Tip 4: Verify Your Results
After completing your calculations:
- Ensure the new shape’s proportions match the original shape; the angles should be the same, and the side lengths should be in the same ratio as the scale factor.
- Use the distance formula or graph paper to verify distances between corresponding points.
Tip 5: Solve with Systematic Approach

Here’s a step-by-step approach to solve dilation problems:
- Identify the given elements: Center of dilation, scale factor, and either the original or the dilated figure.
- Apply the scale factor: Use the provided or deduced scale factor to find new coordinates or distances.
- Sketch if necessary: Drawing the dilation can help visualize the process and verify calculations.
- Check your work: Cross-verify with known results or geometric properties.
Mastering dilation involves not only understanding the concept but also developing a systematic approach to apply it. With these tips, you're equipped to tackle any dilation worksheet with confidence. Each dilation problem you solve helps build your spatial reasoning and geometric intuition, essential skills in higher mathematics.
Remember, practice is key. Don't hesitate to use these tips repeatedly to reinforce your understanding and improve your proficiency in dilation problems. Every worksheet solved is a step closer to geometric mastery.
What if the scale factor is negative?

+
If the scale factor is negative, the figure undergoes dilation and reflection across the center of dilation. The new coordinates will involve both scaling and a change in sign.
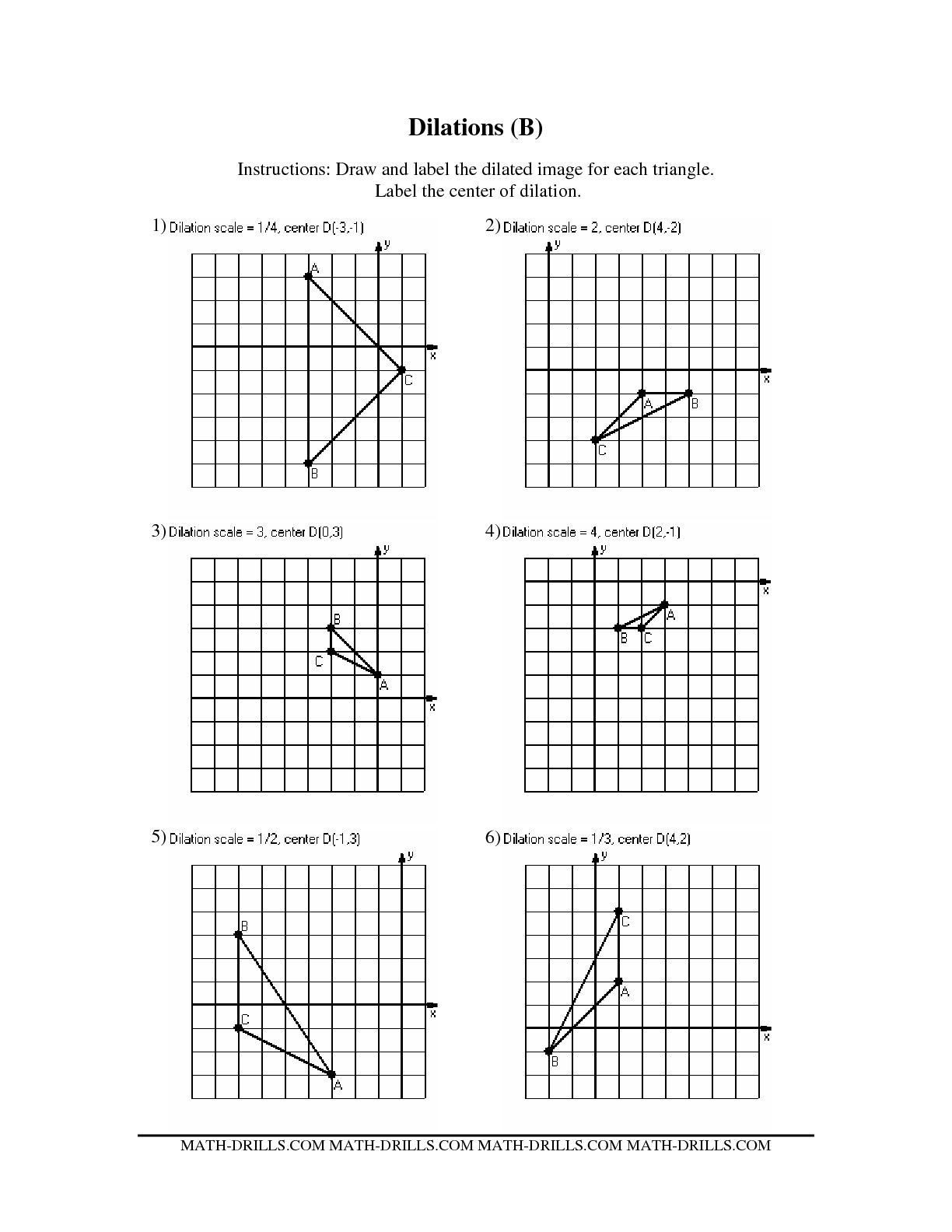
How do you find the center of dilation when it’s not given?
+
To find an unknown center of dilation, you can draw lines connecting corresponding points of the original and dilated figures. The intersection of these lines will be the center.
Can shapes change orientation after dilation?

+
Generally, dilation does not change the orientation of a shape. If you observe a change in orientation, there might be an additional transformation like rotation involved or the problem might be incorrectly described.