Piecewise Functions Worksheet: Master Evaluation with Ease

Understanding Piecewise Functions

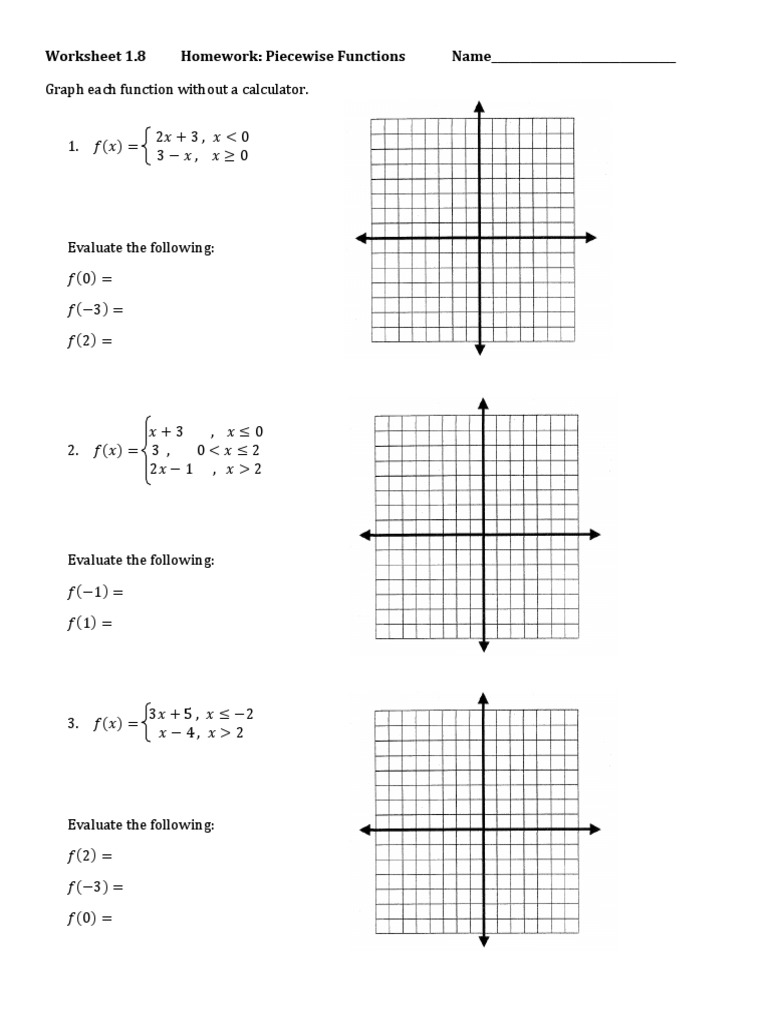
Piecewise functions are a fascinating part of mathematical study, often encountered in higher algebra courses. These functions are defined by multiple sub-functions, each applying to a specific part of the domain. To understand these functions effectively, you need to grasp how each piece of the function operates within its respective interval.
What are Piecewise Functions?

Piecewise functions are functions defined by multiple "pieces", with each piece being active for a specific segment of the domain. Here's how you can identify them:
- They are typically written with conditions or domains stated explicitly for each piece.
- Common notation involves curly braces {} to separate each sub-function.
The Structure

Consider this example:
f(x) = {
- x + 3, for x < 0
- 2x - 1, for 0 ≤ x ≤ 2
- -x + 5, for x > 2
}
Here, we have three different functions for three different domains:
- When x is less than zero, the function is f(x) = x + 3.
- From 0 to 2, f(x) = 2x - 1.
- When x is greater than 2, the function becomes f(x) = -x + 5.
Evaluating Piecewise Functions

To evaluate a piecewise function, follow these steps:
- Determine which piece of the function corresponds to the value of x you are given.
- Use the corresponding sub-function for that piece to find the value of f(x).
💡 Note: Ensure to include the endpoint of the domain if it is included in the piece, as seen in the second piece above.
Example Evaluation

Let's evaluate the function for x = -1, x = 1.5, and x = 3 from the above example:
- For x = -1, since -1 is less than 0, use f(x) = x + 3. So, f(-1) = -1 + 3 = 2.
- For x = 1.5, 1.5 is within the range 0 to 2, so use f(x) = 2x - 1. Thus, f(1.5) = 2 * 1.5 - 1 = 3 - 1 = 2.
- For x = 3, which is greater than 2, we use f(x) = -x + 5. Hence, f(3) = -3 + 5 = 2.
Graphing Piecewise Functions

Graphing piecewise functions can be insightful. Here are the steps:
- Identify each piece's domain.
- Graph each piece individually, ensuring to apply the appropriate domain restrictions.
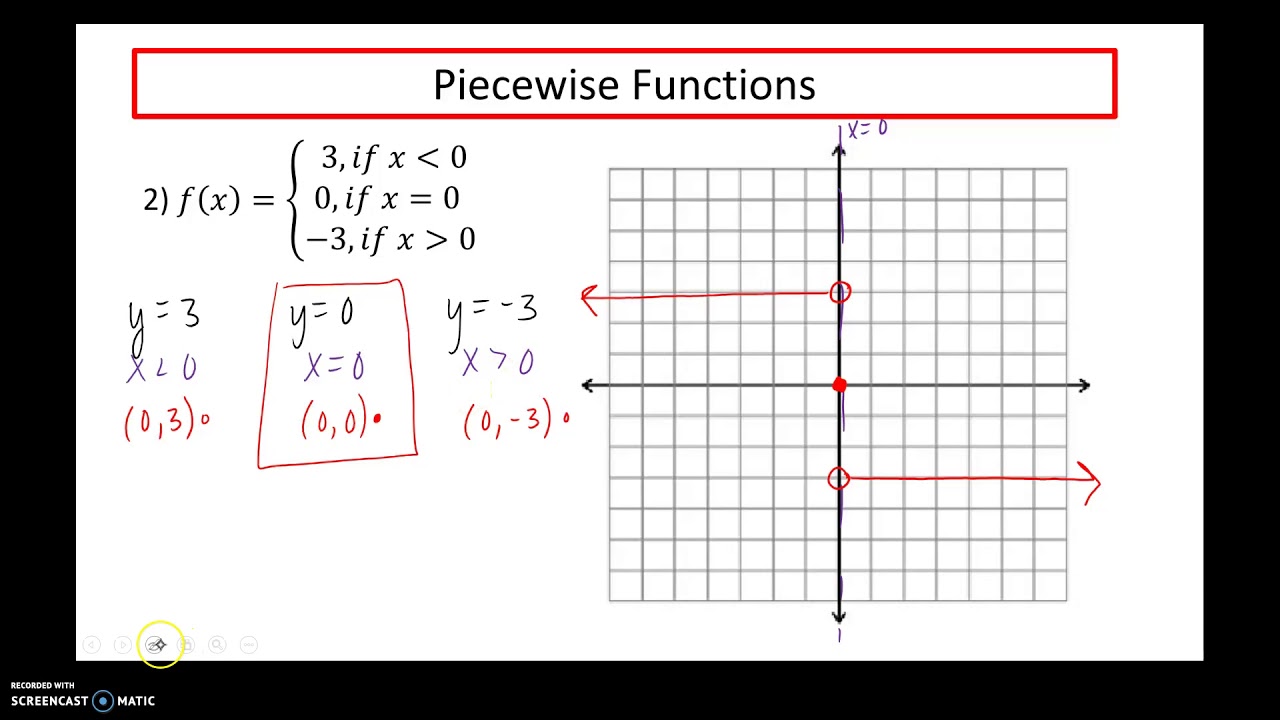
- Connect or plot the points on a graph accordingly, marking endpoints with open or closed circles to indicate inclusion or exclusion.
📌 Note: On a graph, solid dots indicate inclusion, and open circles indicate exclusion of the endpoint.
Applications of Piecewise Functions
Piecewise functions aren't just abstract math; they have real-world applications:
- Tax Brackets: Different tax rates apply to different income levels, creating a piecewise function for tax calculation.
- Electrical Circuits: Piecewise functions can model different behaviors of voltage or current within specific ranges.
- Shipping Costs: Different shipping rates for different weight ranges make for an excellent example of piecewise functions in action.
Worksheet Practice

To master piecewise functions, practice is key. Here's a simple worksheet to help you evaluate them:
| Function | x-value | Answer |
|---|---|---|
| g(x) = {
3x - 2, for x < 0 x + 5, for 0 ≤ x < 3 4, for x ≥ 3 } |
-1 | |
| 1 | ||
| 4 |
Fill in the answers:
- For x = -1, g(-1) = 3*(-1) - 2 = -5.
- For x = 1, which falls between 0 and 3, g(1) = 1 + 5 = 6.
- For x = 4, which is greater than or equal to 3, g(4) = 4.
Thus, our table is filled out:
| Function | x-value | Answer |
|---|---|---|
| g(x) = {
3x - 2, for x < 0 x + 5, for 0 ≤ x < 3 4, for x ≥ 3 } |
-1 | -5 |
| 1 | 6 | |
| 4 | 4 |
Practicing these problems will help you to understand where each piece of a piecewise function applies, ensuring you can evaluate functions quickly and accurately.
Why do we use piecewise functions?

+
Piecewise functions are used to model scenarios where the behavior or conditions change at different intervals. They are useful in situations where different rules or formulas apply based on certain conditions or boundaries.
How do you graph a piecewise function?

+
To graph a piecewise function:
- Plot each piece of the function within its domain.
- Use open or closed circles to indicate endpoint inclusion or exclusion.
- Connect the points for continuous segments or leave gaps for discontinuous parts.
Can piecewise functions have infinite pieces?

+
Technically, yes, piecewise functions can have an infinite number of pieces. However, in practical applications, functions are often defined with a manageable number of pieces for clarity and simplicity.
How do piecewise functions relate to continuity?

+
A piecewise function is continuous if at the points where the pieces meet, the function values match on both sides. If there's a gap or a jump at these points, the function is discontinuous at those points.
What are some common errors in evaluating piecewise functions?

+
Some common errors include:
- Using the wrong piece of the function for a given x-value.
- Misunderstanding the domain restrictions.
- Failing to account for the behavior of the function at the endpoints.
- Not recognizing when a function's piece might intersect or overlap.
Understanding piecewise functions provides an interesting and practical approach to mathematical analysis. By breaking complex situations into manageable parts, they not only simplify calculations but also offer a structured way to visualize and understand how different rules can govern different segments of a domain. Whether for algebraic problem-solving, graphing, or real-world applications, mastering these functions will give you a robust tool for analysis and calculation in numerous contexts.