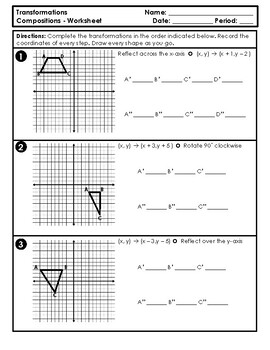
Master Composition of Transformations Worksheet Easily

Transformations in mathematics refer to operations that change the position, size, or shape of a geometric figure. A Master Composition of Transformations Worksheet is an invaluable tool for students and educators to understand how multiple transformations interact. In this comprehensive guide, we'll delve into the steps to master this worksheet, ensuring that you not only complete it with ease but also understand the underlying principles of transformations in mathematics.
Understanding Transformations


Before tackling the worksheet, it’s crucial to understand the basic transformations:
- Translation: Moves every point in a figure the same distance in the same direction.
- Reflection: Flips a figure over a line, creating a mirror image.
- Rotation: Turns a figure around a fixed point by a certain angle.
- Dilation: Enlarges or reduces the size of a figure while maintaining its shape.
The Steps to Master Your Transformations Worksheet
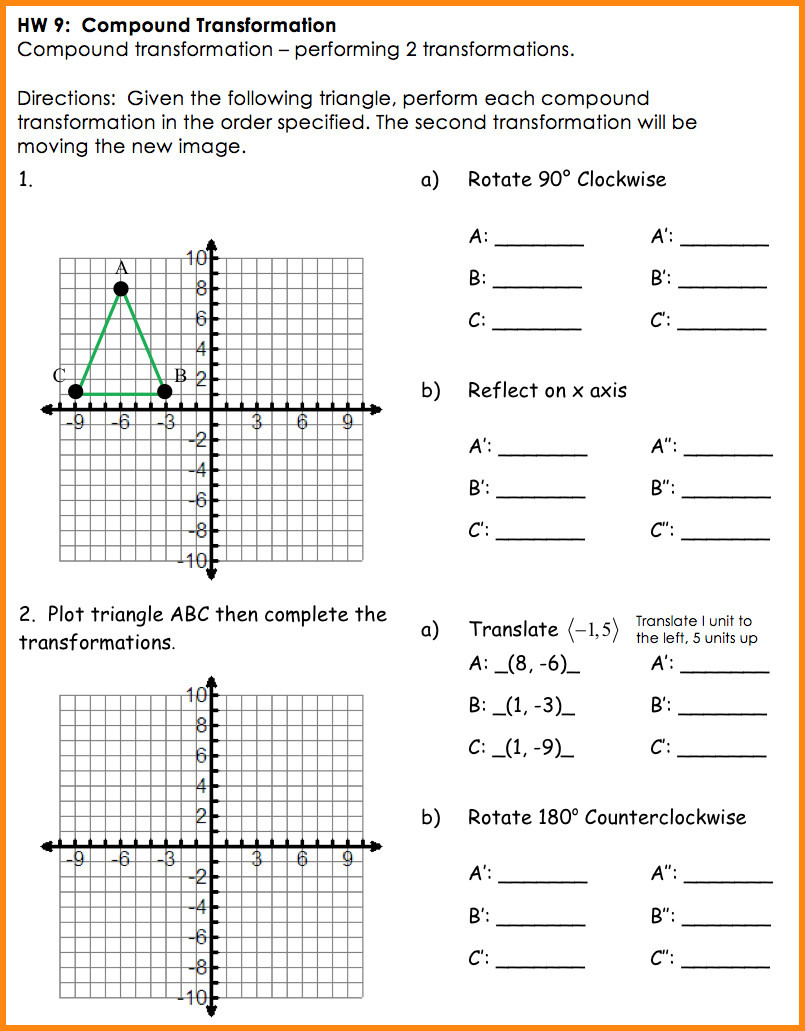
Follow these steps to navigate through your transformation worksheet with precision:
Step 1: Identify the Transformations

Each problem will describe one or several transformations. Here are some tips to identify them:
- Look for keywords like “slide,” “flip,” or “turn” for translations, reflections, and rotations, respectively.
- Check for instructions involving change in size for dilations.
Step 2: Sequence the Transformations

Transformations can be combined in any order, but the order matters due to the commutative nature of some transformations. Here are some tips:
- Determine which transformations must be done first if the problem specifies.
- If there is no specification, consider the typical order: translations, then reflections, followed by rotations, and finally dilations.
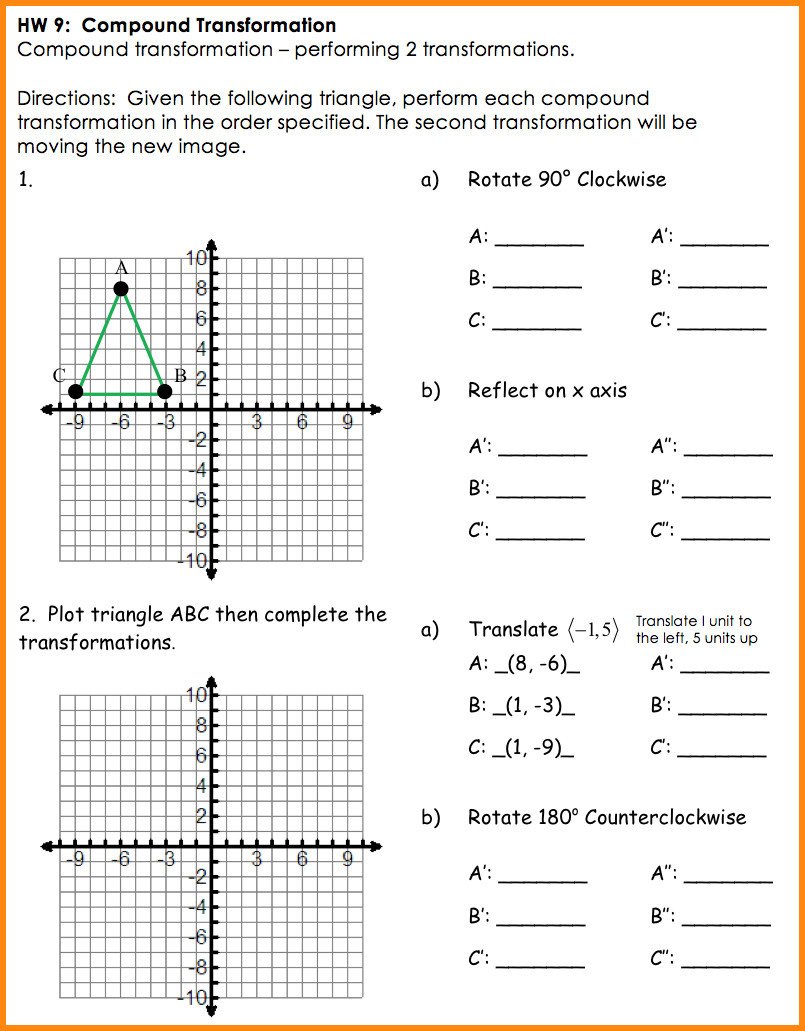
Step 3: Perform Each Transformation
| Transformation | Rule | Example |
|---|---|---|
| Translation | (x, y) → (x + a, y + b) | Move point A from (2, 3) by translation of 3 units right and 2 units up to (5, 5). |
| Reflection | (x, y) → (-x, y) or (x, -y) | Reflect point B over the y-axis from (4, 6) to (-4, 6). |
| Rotation | Varies with center of rotation and angle | Rotate point C 90° counterclockwise around the origin from (3, 1) to (-1, 3). |
| Dilation | (x, y) → (kx, ky) where k is the scale factor | Dilate point D by a factor of 2 from (1, 2) to (2, 4). |

Step 4: Final Position and Shape
After performing all the given transformations:
- Plot the final points on a coordinate grid if necessary.
- Check the shape and orientation to ensure they match the given instructions.
📝 Note: Remember that transformations must be carried out sequentially in the order given. Changing the sequence can lead to different final results.
Tips and Tricks for Success

To master the composition of transformations effortlessly:
- Practice: The more you practice different problems, the more you’ll recognize patterns and shortcuts.
- Use Visual Aids: Draw the transformations step by step if possible. Visualizing helps in understanding the final shape.
- Check Coordinates: Always keep track of the coordinate changes to avoid errors.
The complexity of transformations can initially seem daunting, but with a clear understanding of each step and consistent practice, mastering transformations worksheets can become an enjoyable challenge. It's not just about getting the right answer but also about appreciating the dynamic nature of geometric figures.
In the journey of learning and understanding mathematical concepts, worksheets like the Master Composition of Transformations Worksheet serve as essential tools. They allow us to explore the beauty and logic behind these operations, enabling us to tackle more complex problems with confidence.
Why is the order of transformations important?

+
The order of transformations can change the final position and orientation of the figure due to their non-commutative nature. For example, performing a rotation followed by a reflection does not yield the same result as performing the reflection first and then the rotation.
How can one ensure accuracy when performing transformations?

+
One can ensure accuracy by understanding each transformation rule, meticulously applying these rules in sequence, and double-checking the transformations with a coordinate system or by drawing. Practice and visualizing the steps significantly help in maintaining accuracy.
What are some common mistakes students make with transformations?

+
Common mistakes include:
- Applying transformations in the wrong order.
- Confusing reflection and rotation.
- Incorrectly performing dilations by not using the correct scale factor.
- Not keeping track of coordinates properly, leading to errors in final points.
Can a single worksheet cover all types of transformations?

+
Yes, a well-designed worksheet can incorporate various types of transformations to provide comprehensive practice.
Summing up, mastering the composition of transformations worksheet not only enhances your problem-solving skills but also provides a deeper understanding of geometric figures and their manipulations. Keep practicing, stay organized, and remember the importance of sequencing your transformations, and you’ll soon find yourself adept at handling even the most complex transformation problems.