Mastering Composite Transformations: A Fun Worksheet Adventure
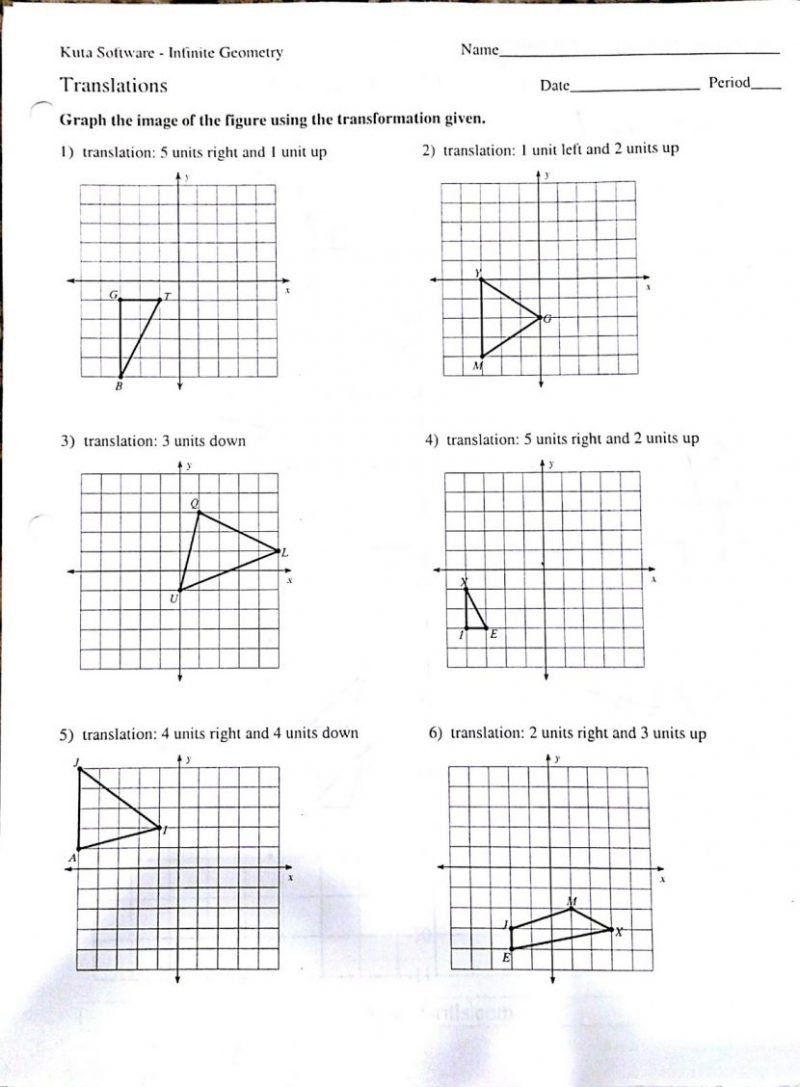
In the world of geometric transformations, composite transformations stand out as a fascinating puzzle where basic moves combine to create complex patterns. Whether you're a student delving into the depths of geometry or a teacher looking to inspire, understanding these transformations is crucial. This blog post will guide you through the journey of mastering composite transformations with a fun worksheet adventure, ensuring that each step taken is a step closer to geometric mastery.
The Basics of Transformations


Before we dive into composites, let’s review the fundamental transformation types:
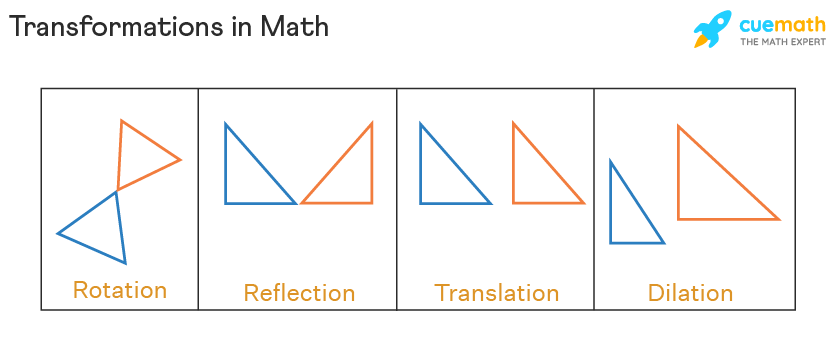
- Translation - Moving every point of a figure a constant distance in a specified direction.
- Rotation - Rotating the figure around a central point.
- Reflection - Flipping the figure over a line.
- Dilation - Scaling the figure up or down while keeping the shape the same.
Understanding Composite Transformations

Composite transformations involve combining two or more basic transformations into one operation. Here’s how they work:
- First, identify each transformation involved.
- Then, apply them in sequence, keeping track of how each transformation changes the coordinates or orientation of the figure.
- Finally, the result of each transformation becomes the input for the next, creating a chain reaction of changes.
The Worksheet Adventure Begins

To truly grasp composite transformations, engaging in practical exercises is invaluable. Here’s how to turn learning into an adventure:
Set the Stage

Print out a worksheet or design one on digital software. Include:
- A coordinate grid.
- Figures to transform (like a triangle, a square, or any recognizable shape).
- Instructions for each composite transformation.
Mapping Your Journey
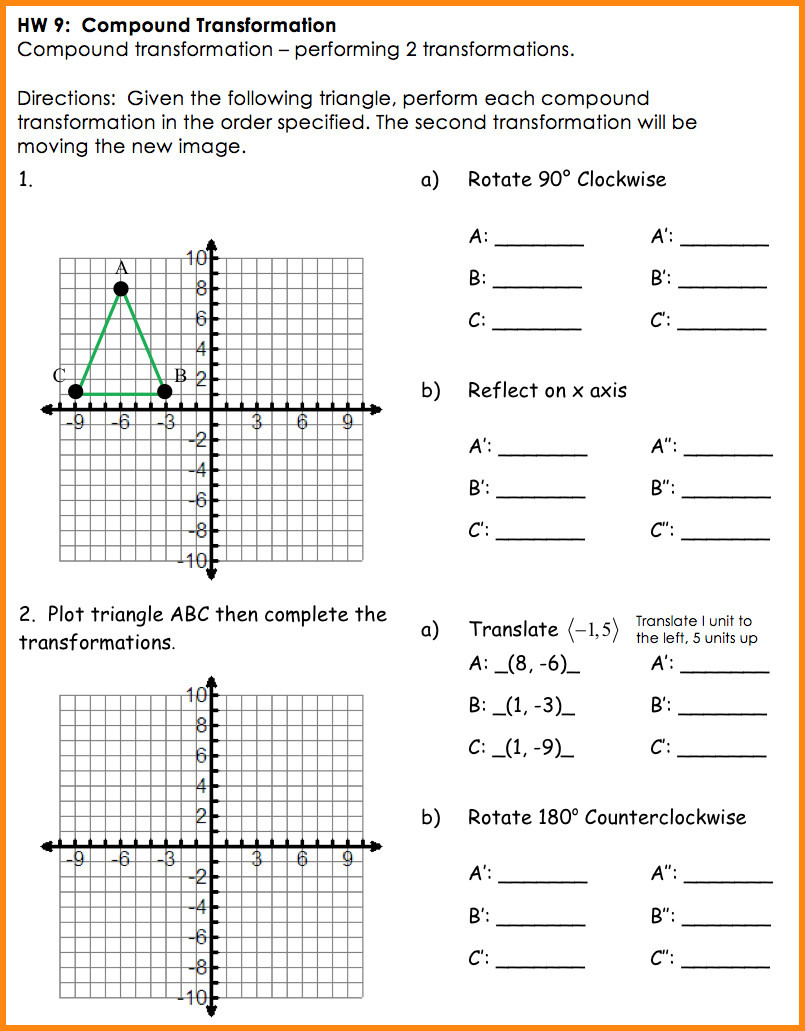
Each transformation in the worksheet can be likened to moving through different landscapes:
- Translation could be a peaceful hike through a straight path in a forest.
- Rotation might mimic a dance move, turning around a specific point or landmark.
- Reflection could be like looking into a mirror, seeing your figure’s “twin” on the other side.
- Dilation could represent entering a fairy circle, either growing or shrinking in size.
The Worksheet Challenge

Here’s an example of what a transformation challenge might look like:
Step Action Notes 1 Translate the triangle 3 units right and 2 units up. Keep the same orientation. 2 Rotate the translated triangle 90 degrees clockwise around point (3,3). Use (3,3) as the pivot point. 3 Reflect the rotated triangle across the y-axis. Flip horizontally. 
🌟 Note: Use different colors or shades to mark each step of the transformation for clarity.
Tips for Effective Learning
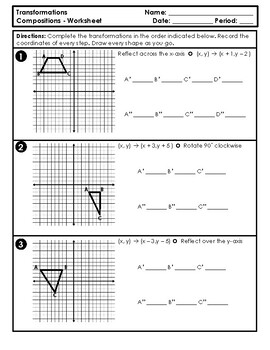
- Color Coding: Use different colors for each transformation to visualize the changes clearly.
- Step-by-Step: Encourage learners to draw each intermediate step, not just the final position.
- Checkpoints: Insert “checkpoints” where learners can verify their progress with provided solutions or hints.
Through this interactive worksheet journey, learners not only become adept at calculating transformations but also visualize how figures move, twist, and evolve through space. It's an exercise in logic, spatial awareness, and the fun of geometry.
In summary, mastering composite transformations is not just about rote learning; it's an adventure in understanding how simple movements come together to create complex, beautiful patterns. By engaging with these transformations in a hands-on manner, learners internalize the concepts, making geometry a subject of discovery and creativity. Whether you're plotting points or adjusting coordinates, each step in this worksheet adventure adds to your geometric toolkit, allowing you to navigate the intricate paths of transformations with confidence.
What are composite transformations?

+
Composite transformations refer to a series of geometric transformations applied to a figure one after another, where the result of each transformation becomes the starting point for the next one.
How do I know the order of transformations matters?
+
The order in which transformations are performed can significantly change the final position of a figure. For example, reflecting a shape first and then translating it will yield a different result compared to translating and then reflecting.
Can composite transformations involve different types of transformations?
+
Yes, composite transformations can involve any combination of translations, rotations, reflections, and dilations, each adding to the complexity and final outcome of the figure’s transformation.



