5 Essential Composite Area Formulas in Geometry

In the world of geometry, understanding and applying the right formulas to calculate areas of various shapes is a fundamental skill. Geometry isn't just about points, lines, and shapes; it's about understanding the space around us. Whether you're tackling academic assignments, designing buildings, or simply solving everyday problems, mastering composite area formulas can save time and enhance accuracy. In this comprehensive guide, we delve into the 5 essential composite area formulas that every student, professional, and geometry enthusiast should know.
The Importance of Composite Areas

Composite shapes or areas arise when two or more geometric figures are combined. Instead of treating these shapes as separate entities, we calculate their areas more efficiently by understanding their combined forms:
- Time Efficiency: Calculating areas in parts can be time-consuming, especially for complex figures.
- Accuracy: Minimize errors by reducing the number of separate calculations.
- Practicality: Real-world applications often involve irregular shapes, making composite formulas invaluable.
1. Composite Rectangle Formula
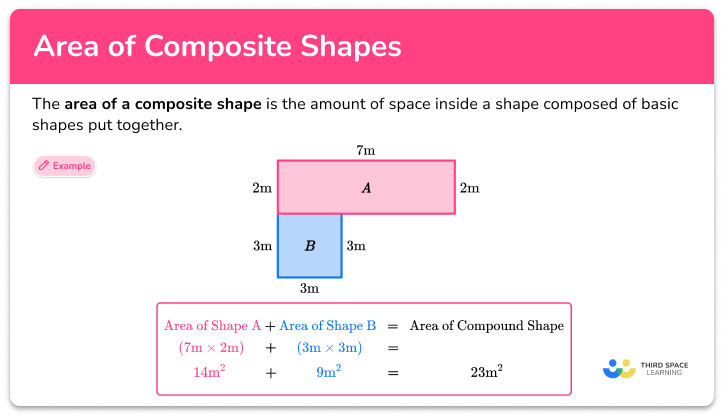

When two or more rectangles are combined, the composite area formula is straightforward:
A = A1 + A2 + … + An
Here, A1, A2, …, An are the areas of the individual rectangles. To find the area of each rectangle:
- Calculate the area of each rectangle using A = Length x Width.
- Add these areas together for the total composite area.
💡 Note: When dealing with irregular shapes formed by rectangles, ensure you’re not double-counting any overlapping areas.
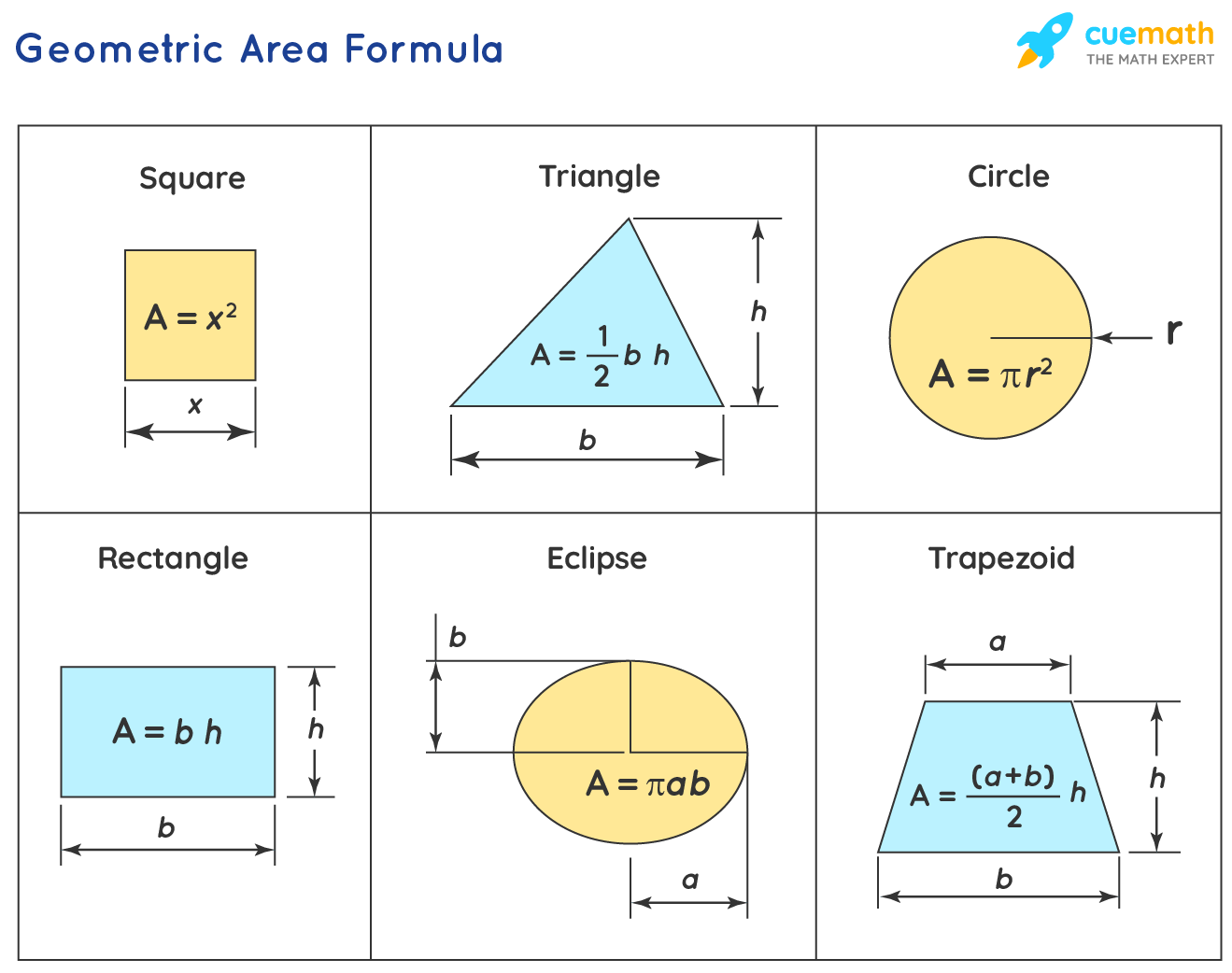
2. Composite Triangle Formula


Triangles can be combined in multiple ways, but the essence remains:
A = A1 + A2 + … + An - (Overlap)
- Calculate the area of each triangle using A = 1⁄2 x Base x Height.
- If there is an overlap, subtract it from the sum of individual triangle areas.
💡 Note: Always determine the type of overlap, whether it’s another triangle, a rectangle, or an irregular shape, to correctly subtract it.
3. Trapezoid and Composite Quadrilaterals

Trapezoids and other quadrilaterals can also be composite figures:
A = 1⁄2 x (b1 + b2) x h
- Here, b1 and b2 are the lengths of the two parallel sides, and h is the height.
- For composite quadrilaterals with no common bases or heights, apply individual formulas or divide into known shapes.
4. Circles and Sectors in Composite Figures
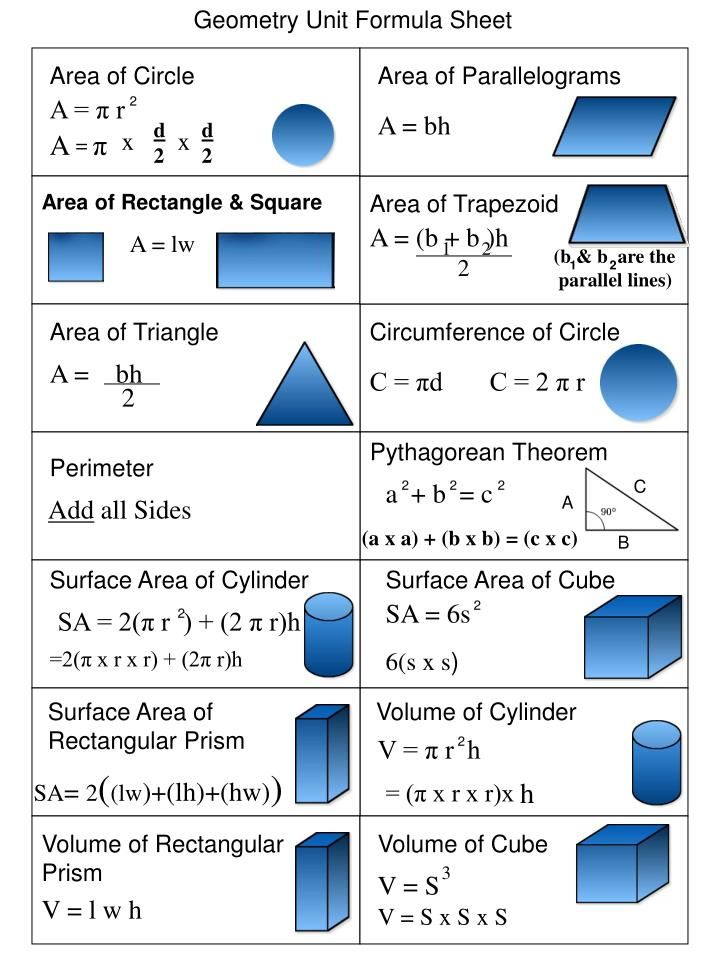

Circular shapes often combine in composite figures:
A = A1 + A2 + … + An - (Overlap)
- Calculate the area of full circles with A = πr² where r is the radius.
- For sectors, A = (θ/360) x πr², where θ is the central angle in degrees.
- Subtract any overlap, which might be another sector, a circle, or another shape.
5. Composite Figures with Irregular Shapes


Some composite figures don’t fit neatly into the above categories:
- Divide the Shape: Break the composite figure into simpler shapes.
- Apply Relevant Formulas: Use formulas from rectangles, triangles, circles, etc.
- Summarize the Areas: Add or subtract areas as necessary, accounting for overlaps.
This comprehensive journey through the essential composite area formulas in geometry equips you with the tools to tackle complex shapes with ease. The beauty of geometry lies in its ability to simplify the seemingly complex through patterns and formulas. By mastering these formulas, not only can you solve academic problems more efficiently, but you also unlock a deeper understanding of the world around us, where composite shapes are omnipresent. Remember, accuracy, efficiency, and understanding the principles behind these formulas are the keys to mastering geometry.
Why is understanding composite areas important in real-world applications?
+
Composite areas are crucial for fields like architecture, engineering, and land surveying where irregular shapes are common. Efficiently calculating areas can save time and resources in designing and planning projects.
Can I use these formulas for three-dimensional objects?

+
While these formulas are primarily for two-dimensional shapes, they can be used to calculate the surface area of three-dimensional objects by considering each face individually or decomposing the shape into simpler forms.
How do I handle composite shapes with very complex boundaries?

+
For very complex shapes, you might need to use specialized software or graphical methods like Simpson’s Rule or the trapezoidal rule, which estimate areas by dividing the shape into smaller, more manageable parts.



