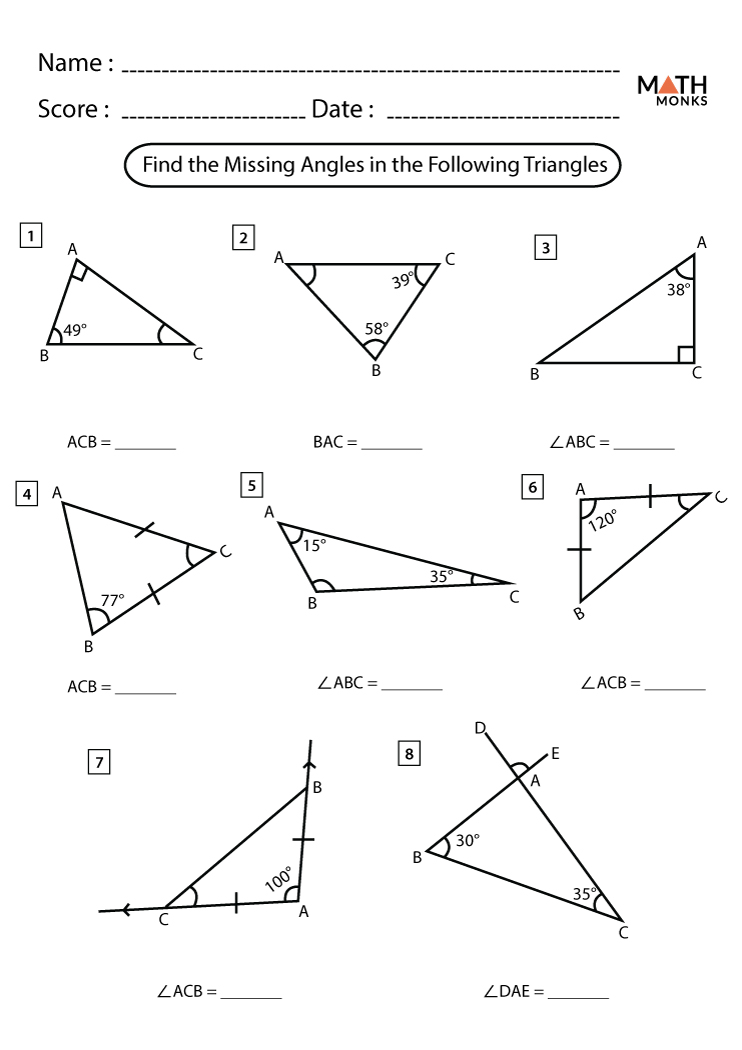
Complementary and Supplementary Angles Practice Sheet
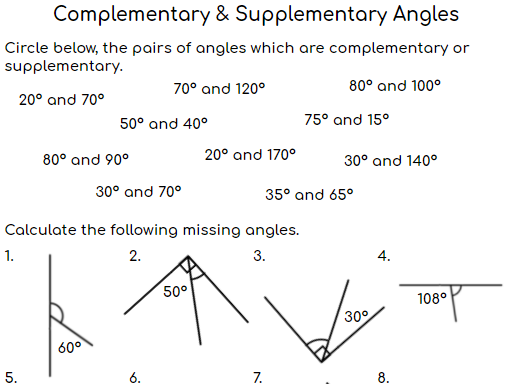
In the world of geometry, angles play a crucial role in defining the relationship between different lines and shapes. Among these, complementary and supplementary angles are fundamental concepts that students often encounter in their math classes. Understanding these angles not only boosts your geometric prowess but also enhances your problem-solving skills. This practice sheet will delve into what these angles are, how they are calculated, and provide you with ample practice to master them.
What Are Complementary Angles?

Complementary angles are two angles whose measures add up to 90 degrees. Here’s a breakdown:
- When two angles sum up to 90 degrees, they are said to be complementary.
- Each angle in a pair of complementary angles is often referred to as the complement of the other.
Here’s how you can recognize them:
- If one angle is given and you need to find its complement, simply subtract that angle from 90 degrees.
- Example: If angle A is 30 degrees, then its complement is 90 - 30 = 60 degrees.
What Are Supplementary Angles?
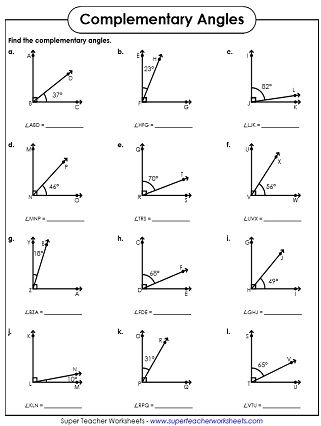
Supplementary angles, on the other hand, are two angles whose measures add up to 180 degrees. Consider these points:
- When the sum of two angles is 180 degrees, these angles are known as supplementary.
- Each angle in this pair is called the supplement of the other.
Here’s how to work with them:
- To find the supplement of an angle, subtract that angle from 180 degrees.
- For instance, if angle B is 120 degrees, then its supplement is 180 - 120 = 60 degrees.
Practice Problems

📝 Note: Remember to draw your angles or imagine them for better understanding.
Problem Set 1: Complementary Angles

| Problem | Solution |
|---|---|
| Find the complement of an angle measuring 40 degrees. | 90 - 40 = 50 degrees |
| If one angle in a pair of complementary angles is 55 degrees, what is the other angle? | 90 - 55 = 35 degrees |

Problem Set 2: Supplementary Angles

| Problem | Solution |
|---|---|
| Determine the supplement of an angle measuring 110 degrees. | 180 - 110 = 70 degrees |
| If one angle in a supplementary pair is 135 degrees, what is the other angle? | 180 - 135 = 45 degrees |
🎨 Note: You can visualize these angles by drawing them on paper, which aids in understanding their spatial relationships.
Advanced Concepts

Beyond simple calculation, understanding complementary and supplementary angles extends into more complex scenarios:
- Adjacent Complementary Angles: These are angles that share a common side and vertex, summing to 90 degrees. They create a right angle together.
- Adjacent Supplementary Angles: These are angles that also share a side and vertex but sum to 180 degrees, forming a straight line.
To apply these:
- Identify if angles are adjacent by checking for a common vertex and side.
- Use properties like linear pairs or vertically opposite angles when solving problems involving these angles.
Conclusion
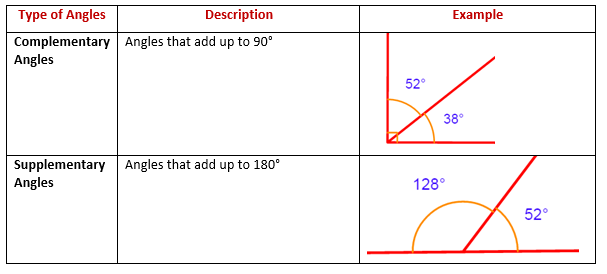
This practice sheet has equipped you with the foundational knowledge of complementary and supplementary angles. From defining them to practicing with real problems, you’ve now seen how these angles relate and how they can be calculated. Remember, these concepts aren’t just theoretical; they apply in various real-world scenarios, like architecture, where understanding angles is crucial for stability and aesthetics. By mastering these angles, you’re not just solving math problems; you’re enhancing your ability to interpret and interact with the physical world.
What is the main difference between complementary and supplementary angles?

+
The primary distinction lies in their sum: complementary angles add up to 90 degrees, while supplementary angles add up to 180 degrees.
Can an angle be both complementary and supplementary?

+
An angle cannot be both complementary and supplementary to another angle at the same time. However, an angle can be part of different pairs where it is complementary to one angle and supplementary to another.
How can understanding angles help in everyday life?

+
Understanding angles is crucial in various practical applications, such as construction, carpentry, navigation, and even in sports like billiards or soccer, where precision in direction and angles can determine success.