Master Comparing Unlike Fractions with Our Worksheet

Understanding and comparing unlike fractions can often pose a challenge for students at various learning levels. This skill, essential for advanced mathematics and practical problem-solving, involves not just recognizing the numerical values but also the relationship between those values. By leveraging our specially designed worksheets, you can navigate this educational journey with ease, improving both understanding and proficiency.
Introduction to Unlike Fractions


Before diving into the intricacies of comparing unlike fractions, let’s define what we mean by unlike fractions. Unlike fractions are fractions that have different denominators, unlike common or like fractions which share the same denominator. When comparing or performing arithmetic operations on unlike fractions, one must first convert them to like fractions, usually by finding a common denominator.
Step-by-Step Guide to Comparing Unlike Fractions

The process of comparing unlike fractions involves a series of logical steps:
- Identify the fractions: Clearly state the fractions you are comparing, e.g., 3/4 and 5/8.
- Find a common denominator: The goal here is to find a common denominator that the fractions can share, making them comparable. This can often be the least common multiple (LCM) of the denominators.
- Convert to like fractions: Using the common denominator, convert each fraction to an equivalent fraction with this denominator.
- Compare the numerators: Once the fractions share the same denominator, comparing the numerators will give you the answer.
- State the result: Based on the comparison, state which fraction is larger, smaller, or if they are equal.
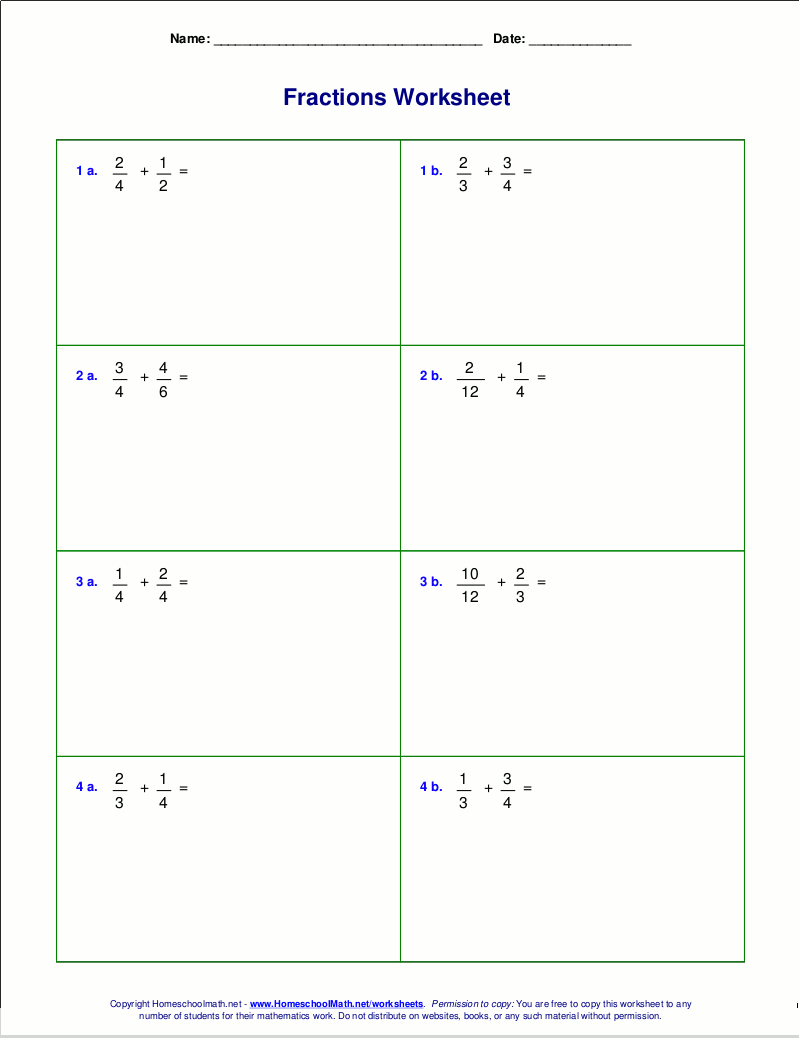
Worksheet Exercises

Here are some example exercises from our comparing unlike fractions worksheet:
| Problem | Solution |
|---|---|
| Compare 2/5 and 3/4 | Since 2/5 and 3/4 have different denominators, we need to find a common denominator. The LCM of 5 and 4 is 20. Converting:
|
| Compare 1/3 and 2/6 | Both fractions can share the common denominator 6. Converting:
|
| Compare 5/7 and 7/10 | The LCM of 7 and 10 is 70. Converting:
|
🔥 Note: Always verify the conversion by multiplying both the numerator and the denominator by the same number to ensure the value remains unchanged.
As you work through these exercises, note the following tips:
- When comparing fractions with significantly different denominators, using multiples or LCM can make the process more manageable.
- Practice recognizing when fractions are already in their simplest form to save time during conversion.
Common Pitfalls and How to Avoid Them

Here are some common mistakes students make when comparing unlike fractions:
- Misinterpreting cross multiplication: Ensure you understand the difference between converting to like fractions and cross multiplying; the former is essential for our approach.
- Ignoring simplification: Simplifying the fractions to their lowest terms before or after conversion can avoid confusion.
- Forgetting zero: Remember, if the denominator is zero, the fraction is undefined.
- Neglecting negative signs: If you're dealing with negative fractions, don't forget to consider the sign when comparing.
📣 Note: Working with different denominators requires patience and a good understanding of multiplication and division. Practice with worksheets will help build these skills.
As you progress in your mathematical journey, mastering unlike fractions can pave the way for tackling more complex problems in algebra, geometry, and beyond. This knowledge not only enhances your academic skills but also your ability to make informed decisions in everyday life, from cooking to finance.
Recapping our journey through this guide:
- We introduced the concept of unlike fractions.
- We walked through a detailed step-by-step guide on how to compare these fractions.
- We provided exercises for you to practice, highlighting the importance of common denominators.
- We discussed common pitfalls and how to avoid them, offering tips for smoother learning.
Now, let's dive into some frequently asked questions to further illuminate the subject:
Why can’t we compare unlike fractions directly?

+
Unlike fractions have different denominators, making direct comparison impossible. Converting them to like fractions with a common denominator allows us to see the relationship between their numerators, thus comparing their values accurately.
What’s the easiest way to find a common denominator?

+
The most efficient method is finding the least common multiple (LCM) of the denominators. This ensures you’re not working with unnecessarily large numbers, making the comparison more straightforward.
How does comparing unlike fractions help in real life?
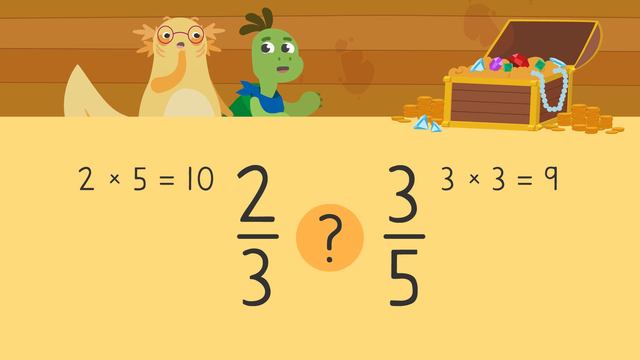
+
Comparing unlike fractions can help in various real-life scenarios, from comparing ingredients when cooking to understanding ratios in financial calculations, making choices about proportions in design, or interpreting data with different scales.
Can I use decimals to compare unlike fractions?

+
Yes, converting fractions to decimals is another method to compare them. However, this can sometimes lead to complex decimal fractions, so using common denominators is often simpler and more precise for educational purposes.
What if one fraction has a very large denominator?

+
If one denominator is significantly larger, it might be impractical to find an LCM or convert to a common denominator. In such cases, simplification, dividing the numerator and denominator by a common factor, can make the comparison more manageable.
Related Terms:
- Comparing unlike fractions worksheet pdf
- Comparing fractions Worksheet with answers
- Comparing fractions Worksheet Grade 6
- Comparing fractions Worksheet Grade 5



