Master Chain Rule Derivatives with Our Worksheet
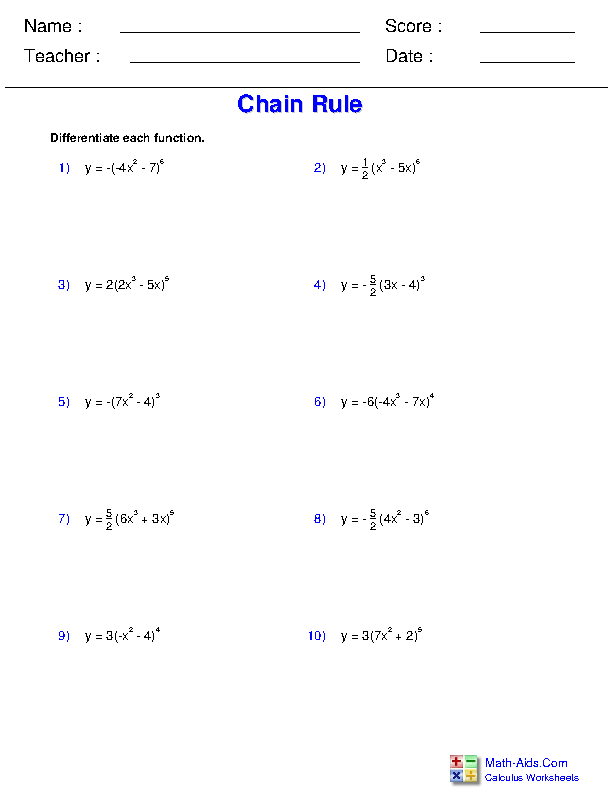
Understanding the Chain Rule

The chain rule is a fundamental concept in calculus, often used when dealing with composite functions. Essentially, it helps you differentiate functions within functions. If you have a function like f(g(x)), the chain rule states that the derivative of this composite function with respect to x is:
f’(g(x)) * g’(x)
This rule is essential for solving problems in advanced calculus, physics, and various engineering applications where functions are nested.
How to Use the Chain Rule
Here’s a step-by-step guide on applying the chain rule:
- Identify the Outer and Inner Functions: Recognize which part of your composite function is the outer function and which is the inner function. For example, in sin(3x), sin() is the outer function, and 3x is the inner.
- Differentiate the Outer Function: Find the derivative of the outer function with respect to its argument, treating the inner function as the variable.
- Differentiate the Inner Function: Now, find the derivative of the inner function with respect to the variable x.
- Multiply the Results: Multiply these two derivatives together. This is the chain rule in action.
Example:

Let’s take f(x) = sin(3x). Here, f(u) = sin(u) and u = 3x.
- The derivative of sin(u) is cos(u).
- The derivative of 3x is 3.
- So, the derivative of sin(3x) with respect to x is cos(3x) * 3 = 3cos(3x).
💡 Note: It’s crucial to keep track of which function you are differentiating with respect to at each step.
Chain Rule Worksheet

Practicing with a worksheet helps reinforce understanding. Here’s a table with some exercises for you to practice:
| Exercise | Function to Differentiate | Solution |
|---|---|---|
| 1 | cos(5x) | -5sin(5x) |
| 2 | e^(2x) | 2e^(2x) |
| 3 | ln(x^3) | 3/x |
| 4 | sin(x^2 + 1) | 2x * cos(x^2 + 1) |
| 5 | (x^2 - 3x + 1)^(1⁄2) | (x-1.5)/sqrt(x^2 - 3x + 1) |

Importance of the Chain Rule in Real-World Applications

The chain rule is not just a theoretical tool; it has numerous applications:
- Physics: It’s used to determine rates of change in physical systems, like changes in position, velocity, or acceleration over time.
- Engineering: Engineers use it in control systems, signal processing, and fluid dynamics to model and predict system behavior.
- Economics: Economists apply the chain rule to understand the relationship between multiple factors influencing economic outputs.
Common Mistakes When Applying the Chain Rule

Here are some common pitfalls students encounter:
- Misidentifying the Functions: Students often mix up which function is considered the outer and which the inner.
- Forgetting the Inner Function Derivative: Omitting the derivative of the inner function can lead to incorrect results.
- Calculation Errors: Simple calculation mistakes can significantly affect the outcome, especially with more complex functions.
🧠 Note: Always double-check the functions’ order and calculate step-by-step to avoid errors.
In summary, mastering the chain rule opens up a broader understanding of calculus and its applications. It’s a key skill for anyone dealing with functions and their derivatives, providing the tools to tackle complex real-world problems. Whether you’re dealing with changes in velocity, analyzing economic models, or optimizing engineering systems, the chain rule is your ally. Practice is the pathway to proficiency, so use the worksheet provided to enhance your skills and ensure you’re ready for any calculus challenge.
What if my function has more than two nested functions?

+
The chain rule can be extended to functions with multiple layers of nesting. For f(g(h(x))), you’d apply the chain rule twice: f’(g(h(x))) * g’(h(x)) * h’(x).
Is the chain rule used in any real-world contexts?

+
Absolutely. It’s essential in physics for related rates problems, in economics for understanding multi-variable impacts, and in computer graphics for rendering complex scenes.
Can the chain rule be applied to implicit differentiation?
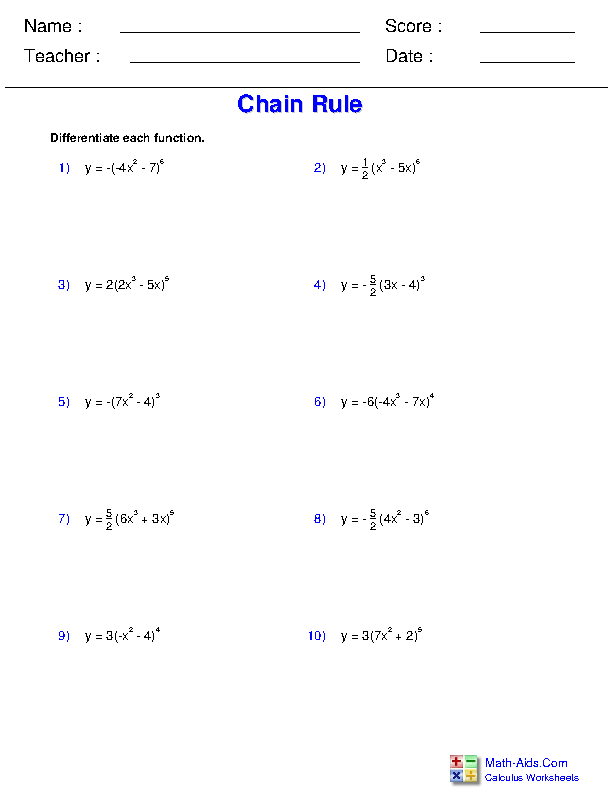
+
Yes, the chain rule is fundamental in implicit differentiation where you might need to find dy/dx for functions where y is implicitly defined.