5 Ways to Solve Missing Sides in Right Triangle Trig

Geometry, particularly the study of triangles, forms the bedrock of mathematical understanding in numerous fields, from engineering to architecture, and even in everyday life. Understanding right triangle trigonometry is particularly useful, as it provides methods to solve for unknown sides or angles when only certain measurements are known. In this blog post, we'll explore five practical ways to calculate missing sides in a right triangle using trigonometric principles.
Understanding the Basics of Trigonometry in Right Triangles

Before diving into the methods, let's establish some foundational knowledge:
- Right Triangle: A triangle with one angle measuring 90 degrees.
- Opposite and Adjacent: Sides relative to a given angle in a right triangle. The side opposite the angle is labeled 'opposite', and the side next to it (excluding the hypotenuse) is 'adjacent'.
- Hypotenuse: The longest side, opposite the right angle.
- Trigonometric Ratios: Sine (sin), Cosine (cos), and Tangent (tan).
Method 1: Using Pythagorean Theorem
The Pythagorean theorem is perhaps the most straightforward method to find the hypotenuse or one of the legs of a right triangle:
\[c^2 = a^2 + b^2\]
Where a and b are the legs, and c is the hypotenuse.
Example:

Given a triangle with legs of 3 and 4 units:
[c^2 = 3^2 + 4^2]
[c = \sqrt{9 + 16} = \sqrt{25} = 5]
📐 Note: This method works only for finding the hypotenuse or a leg when the other two sides are known. For angles, you'll need trigonometry.
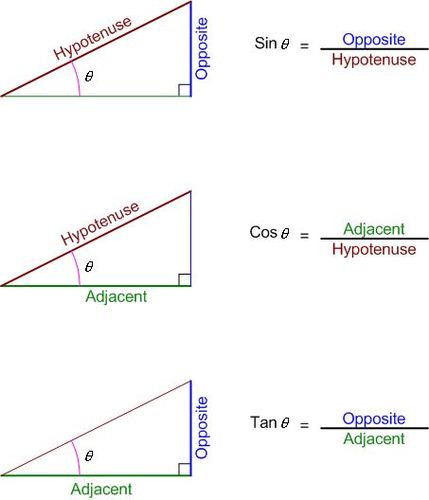
Method 2: Using SOH-CAH-TOA

SOH-CAH-TOA provides a mnemonic to remember the relationships between angles and sides:
- SOH (Sin θ = Opposite / Hypotenuse)
- CAH (Cos θ = Adjacent / Hypotenuse)
- TOA (Tan θ = Opposite / Adjacent)
Example:
If the angle adjacent to a known side is 30° and the adjacent side is 5 units:
\[cos(30^\circ) = \frac{adjacent}{hypotenuse}\]
\[hypotenuse = \frac{adjacent}{cos(30^\circ)} = \frac{5}{\frac{\sqrt{3}}{2}} ≈ 5.77\]
Method 3: Using Inverse Trigonometry

When you need to find an angle, knowing the sides can lead you to the inverse trigonometric functions:
- Arcsine (Sin⁻¹)
- Arccosine (Cos⁻¹)
- Arctangent (Tan⁻¹)
Example:

If you have a triangle with an opposite side of 7 units and an adjacent side of 6 units:
\[θ = Tan⁻¹( \frac{opposite}{adjacent} ) = Tan⁻¹( \frac{7}{6} ) ≈ 49.4^\circ\]
Method 4: Using the Law of Sines
Although not specifically for right triangles, the law of sines can be applied when additional information is given:
\[ \frac{a}{sin(A)} = \frac{b}{sin(B)} = \frac{c}{sin(C)} \]
This method can solve for sides or angles in any triangle, not just right ones.
Method 5: Using Geometry of Similar Triangles

Sometimes, you can use the properties of similar triangles:
- If two triangles have the same angles, their corresponding sides are proportional.
- This method is especially handy when you can't use trigonometry directly.
Example:

If triangle ABC is similar to triangle DEF, and AB = 6 units, DE = 4 units, and DF is 9 units:
\[ \frac{AB}{DE} = \frac{BC}{EF} \]
\[ \frac{6}{4} = \frac{BC}{9} \Rightarrow BC = \frac{6 \times 9}{4} = 13.5 \]
What if I only know one side and one angle of a right triangle?

+
You can use SOH-CAH-TOA to find the other sides or inverse trigonometry to find the angle.
Can the Pythagorean theorem be used for non-right triangles?

+
No, the Pythagorean theorem applies only to right triangles. For other triangles, you might use the Law of Cosines.
Why is trigonometry useful in real-life applications?

+
Trigonometry is fundamental in fields like navigation, architecture, surveying, and engineering, where understanding angles and distances is critical.
In summary, solving for missing sides in a right triangle can be done through a variety of mathematical approaches, each with its own utility depending on the information at hand. From the simplicity of the Pythagorean theorem to the elegance of SOH-CAH-TOA and beyond, these methods not only make mathematical calculations possible but also enhance our understanding of spatial relationships in practical contexts. Whether you’re constructing buildings, navigating seas, or just solving a geometric puzzle, these trigonometric techniques are indispensable tools in your mathematical toolkit.