Centers of Triangles Worksheet Answer Key Revealed

In the realm of geometry, understanding centers of triangles is crucial for both students and enthusiasts of mathematics. This detailed exploration will not only reveal answers to common worksheet problems but also delve into the significance and applications of these triangle centers. Whether you're preparing for an exam or simply indulging in geometric curiosity, let's unravel the magic of triangle geometry together.
What Are the Centers of Triangles?
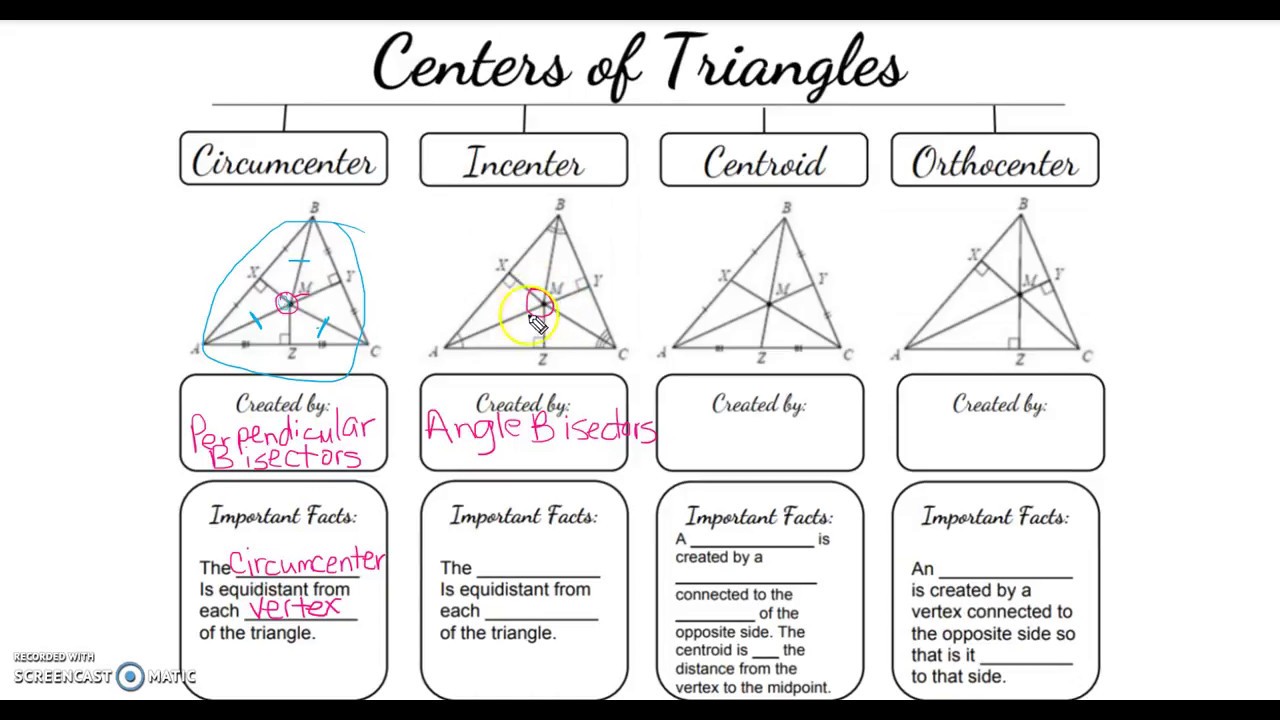
Every triangle, regardless of its shape, boasts several interesting points known as centers. Here are the key centers:
- Circumcenter - The point where the perpendicular bisectors of the sides meet.
- Incenter - The intersection of the angle bisectors of the triangle.
- Orthocenter - Where the altitudes of the triangle converge.
- Centroid - The balance point or the average of all three vertices.
- Excenter - Each of the three excenters is the center of the excircle opposite one of the triangle’s vertices.
📐 Note: The circumcenter, incenter, and centroid always lie inside the triangle, while the orthocenter can be outside if the triangle is obtuse.
Circumcenter and Its Properties
The circumcenter (O) is equidistant from all vertices of the triangle. Here are some notable properties:
- It’s the center of the circle that passes through all three vertices (circumcircle).
- The distance from O to any vertex is the circumradius ®.
- In an equilateral triangle, the circumcenter coincides with the incenter, centroid, and orthocenter.

Incenter and Its Role

The incenter (I) is another critical point in triangle geometry:
- It’s the center of the triangle’s inscribed circle or incircle.
- The incenter equidistant from each side of the triangle, with this distance being the inradius ®.
- The incenter’s coordinates can be found using trigonometric relationships or by solving a system of equations derived from the angle bisectors.

Orthocenter and the Geometry of Altitudes

While the orthocenter (H) might seem less intuitive at first:
- The orthocenter is where the three altitudes of the triangle meet.
- In an acute triangle, the orthocenter lies inside, in an obtuse triangle it’s outside, and on the hypotenuse for a right triangle.
- For an isosceles triangle, the orthocenter, circumcenter, incenter, and centroid lie on the altitude drawn to the base.

Centroid: The Balancing Point

The centroid (G) of a triangle has several unique characteristics:
- It divides each median into a ratio of 2:1, with the centroid being closer to the vertex.
- The centroid is the center of mass for an evenly weighted triangular object.
- The centroid’s coordinates can be calculated using the average of the vertices’ coordinates.

Excenters: Beyond the Triangle
The excenters, although not as celebrated as other centers, offer intriguing insights:
- Each excenter is the center of an excircle, which is tangent to one side of the triangle and the extensions of the other two sides.
- The triangle formed by connecting the excenters is the intouch triangle of the original triangle.
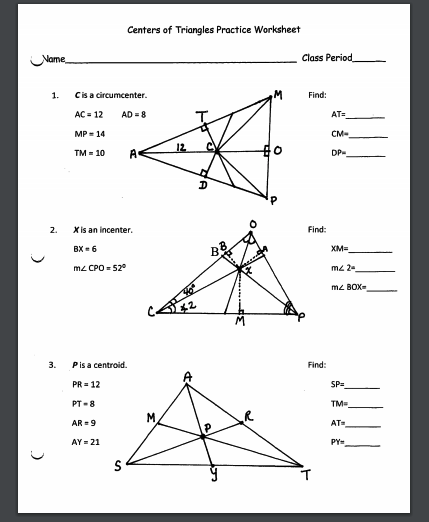
Worksheet Problems and Their Answers

To aid your understanding, here are some common questions found in triangle centers worksheets:
| Problem | Answer |
|---|---|
| Find the coordinates of the circumcenter for a triangle with vertices (0,0), (6,0), (3,3). | Circumcenter coordinates: (3, 1.5) |
| Determine the orthocenter for a triangle with vertices (1,1), (3,3), (5,1). | Orthocenter coordinates: (3, 1) |
| Calculate the centroid of the triangle whose vertices are (0,3), (6,3), (3,6). | Centroid coordinates: (3, 4) |

📐 Note: For complex triangle configurations, computational geometry might be required to find precise coordinates of triangle centers.
Wrapping up, this exploration of triangle centers not only highlights their unique properties but also underscores their role in the fabric of geometry. Understanding these centers allows for a deeper appreciation of the intricate relationships within a triangle, whether you're solving a problem or appreciating geometric elegance. With these key concepts in mind, delve into geometric problems with confidence, knowing that at the heart of every triangle lies a network of points, each with its own story and significance.
Why are triangle centers important?
+
Triangle centers are fundamental in various geometric constructions and have applications in engineering, architecture, and design. They help in understanding the internal structure and balance of triangles, which are critical in stability analysis and structural integrity assessments.
What is the practical significance of the centroid?

+
The centroid is the balancing point of a triangle, making it essential in physics for calculating the center of mass. It’s also used in engineering to determine load distribution on triangular shapes.
Can all centers of a triangle coincide?

+
Yes, in an equilateral triangle, all four main centers - circumcenter, incenter, centroid, and orthocenter - coincide, showcasing the triangle’s perfect symmetry.



