Free Box Method Multiplication Worksheet for Easy Learning

Multiplication, a fundamental arithmetic operation, often presents a learning curve for students. Traditional methods of multiplication can sometimes be confusing, especially when dealing with larger numbers. However, the Box Method, also known as the grid method or area model, simplifies this process by breaking down the multiplication into more manageable steps. This blog post delves into how the Box Method can be an effective educational tool, providing a clear guide on creating a Free Box Method Multiplication Worksheet to facilitate easy learning.
Why Choose the Box Method?

The Box Method, due to its visual and structured approach, is particularly advantageous for several reasons:
- Visual Understanding: It helps students see how numbers are being multiplied, which fosters a deeper understanding of what multiplication actually is.
- Less Intimidating: For students struggling with the vertical format of traditional multiplication, this method reduces anxiety by laying out numbers in a less intimidating manner.
- Facilitates Partial Product Calculations: By breaking multiplication into smaller steps, it makes the process less abstract.
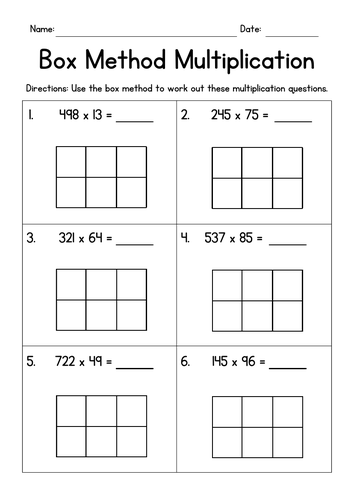
How to Create a Box Method Multiplication Worksheet

To create an effective and engaging Box Method Multiplication worksheet:
Step 1: Choose Your Multiplication Problem

Select a multiplication problem, such as 24 x 35, that will demonstrate the Box Method clearly. Make sure to start with smaller numbers if the worksheet is aimed at beginners.
Step 2: Draw the Grid

Create a grid where the number of rows and columns corresponds to the digits in the multiplicands:
- For 24 x 35, you would need a 2x2 grid.
- The rows represent the tens and ones place of the first number.
- The columns represent the tens and ones place of the second number.
| X | 3 | 5 |
| 2 | ||
| 4 |

Step 3: Fill in the Grid

Multiply the numbers corresponding to the row and column headings and place the results in each cell:
- 2 x 3 = 6 (Tens place of 24 times tens place of 35)
- 2 x 5 = 10 (Tens place of 24 times ones place of 35)
- 4 x 3 = 12 (Ones place of 24 times tens place of 35)
- 4 x 5 = 20 (Ones place of 24 times ones place of 35)
| X | 3 | 5 |
| 2 | 6 | 10 |
| 4 | 12 | 20 |
Step 4: Add and Sum

Now, sum up all the numbers in the grid to find the product:
- 6 + 10 = 16 (sum of tens)
- 16 x 10 = 160 (tens place answer)
- 12 + 20 = 32 (sum of ones)
- 160 + 32 = 192 (final product)
Step 5: Add Instructions
Provide clear instructions on how to use the worksheet, like filling in the grid, adding partial products, and calculating the final answer.
📝 Note: Encourage students to calculate each cell on their own before looking at the provided answer to ensure understanding.
Creating a worksheet using the Box Method can be both educational and fun, providing a hands-on way for students to grasp the concept of multiplication. Here's a summary of how this method benefits learners:
- It visually deconstructs multiplication, making the process more tangible.
- It allows for step-by-step calculation, reducing the chance of mistakes.
- It can be easily adapted for larger numbers, reinforcing the method's versatility.
Using the Box Method in Different Scenarios

While the Box Method is excellent for multiplication, its utility extends to:
- Division: By reversing the process, students can divide using a similar grid format.
- Polynomials: Algebra students find it particularly useful for multiplying polynomials by setting up a similar grid.
- Fractions: The method can be adapted to teach multiplying fractions, giving a concrete understanding of multiplication of rational numbers.
Remember, adapting this method for different mathematical operations or learners of different skill levels can be an engaging and effective way to teach math.
As we wrap up our discussion on the Box Method, let's consider its broader impact on learning:
The Box Method isn't just a tool for multiplication. It's a teaching method that fosters an intuitive understanding of mathematical concepts, making abstract operations more relatable and manageable for students. By breaking down complex calculations into visual and smaller steps, learners can build confidence in their math skills, which often translates into a love for the subject. The method can be a stepping stone towards deeper mathematical understanding, paving the way for students to tackle more complex problems with ease.
What age groups benefit most from the Box Method?

+
The Box Method is particularly beneficial for students in elementary and middle school, typically from ages 7 to 14, as they are learning basic multiplication and algebraic concepts. However, its principles can also be adapted for older students struggling with certain aspects of mathematics.
How does the Box Method compare to the traditional method?

+
The Box Method breaks down multiplication into partial products, which can be less intimidating and more conceptual than the traditional vertical method. It promotes understanding rather than rote memorization, although traditional methods are also valuable for speed and efficiency in calculations.
Can the Box Method be used for division?

+
Yes, the Box Method can be adapted for division by setting up a grid where the divisor and dividend are broken down into parts, and students can then work through the division process step by step in a more visual format.