Free Area Triangle Worksheet for Quick Math Practice

Welcome to our comprehensive resource on triangle areas, tailored to enhance your mathematical proficiency with engaging practice worksheets. This in-depth guide will navigate you through understanding triangle areas, offering both theoretical insights and hands-on exercises designed to solidify your grasp of this fundamental geometric concept.
Understanding Triangle Area
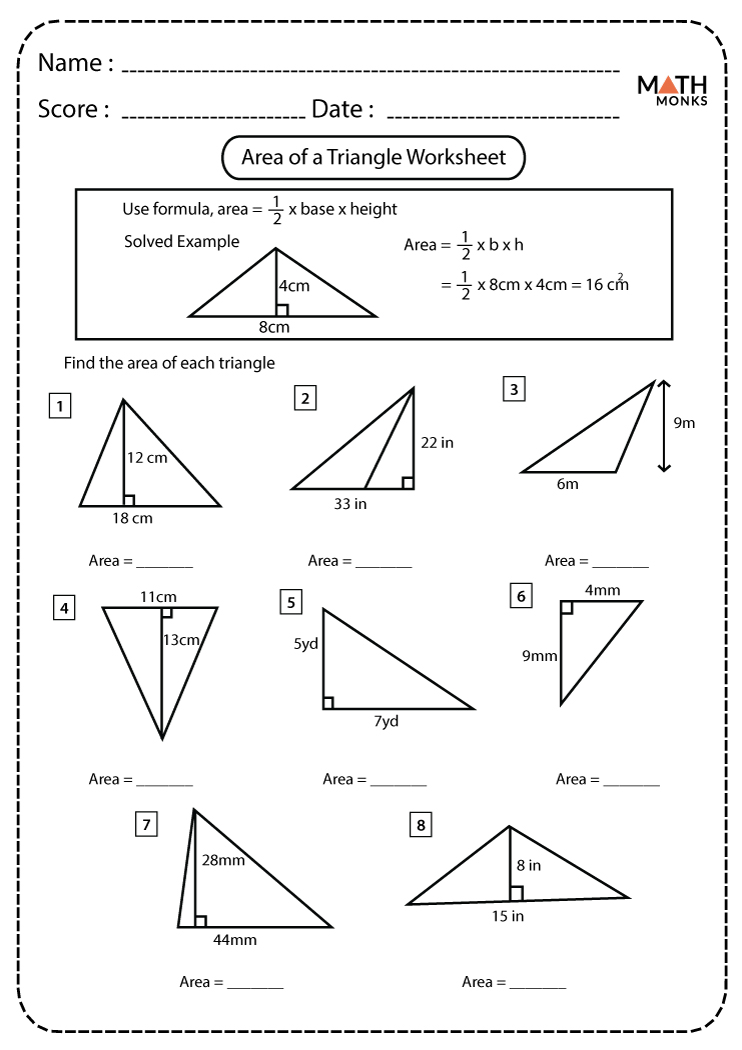
Before diving into the worksheets, it's pivotal to understand how to calculate the area of a triangle. The basic formula for finding the area of a triangle is:
A = (base × height) / 2
Where:
- Base - Any side of the triangle.
- Height - The perpendicular distance from the base to the opposite vertex.
Basic Triangle Area Worksheet

To get you started, here's a simple worksheet to practice calculating triangle areas:
| Base | Height | Area |
|---|---|---|
| 4 cm | 3 cm | (4 × 3) / 2 = 6 cm2 |
| 6 cm | 5 cm | (6 × 5) / 2 = 15 cm2 |
| 8 cm | 7 cm | (8 × 7) / 2 = 28 cm2 |

📝 Note: Remember to always use the correct units of measurement in your answers.
Advanced Techniques for Calculating Triangle Area

Calculating the area of triangles isn't confined to the base and height approach; there are several advanced techniques:
- Using Heron's Formula: This method calculates the area when the side lengths of a triangle are known but not the height.
- Trigonometry: Employing sine and cosine for areas in obtuse and acute angles.
- Coordinate Geometry: If the vertices of the triangle are known as coordinate points, use them to find the area.
Worksheet with Heron's Formula

Here's a practice worksheet using Heron's formula:
| Side 1 | Side 2 | Side 3 | Area |
|---|---|---|---|
| 3 cm | 4 cm | 5 cm | √[s(s-3)(s-4)(s-5)], where s = (3+4+5)/2 = 6 |
✏️ Note: Ensure you accurately calculate 's', the semiperimeter, before applying the formula.
Intersecting Triangles

Sometimes, triangles intersect or are placed within larger shapes. Calculating areas in such scenarios can be challenging. Let's look at a few examples:
- Overlapping Triangles: When two triangles share an area, you subtract the common area from the sum of individual areas.
- Nested Triangles: If one triangle is entirely inside another, subtract the smaller area from the larger one.
Practice Worksheet for Intersecting Triangles

Try these problems where triangles intersect:
| Triangle Description | Area Calculation |
|---|---|
| Triangle ABC with base AB = 5 cm and height from C = 4 cm. Triangle DEF with base DE = 4 cm and height from F = 3 cm, where DEF intersects ABC at points E and F. | Area ABC = (5 × 4) / 2 = 10 cm2, Area DEF = (4 × 3) / 2 = 6 cm2, Total Area = 10 + 6 - 2 (common area) = 14 cm2 |
FAQs on Triangle Area Calculations

Can I use any side of the triangle as the base for area calculation?

+
Yes, any side of the triangle can be considered the base for calculating its area, provided you measure the height from that base correctly.
What if the triangle is not right-angled?

+
Non-right-angled triangles require using techniques like Heron's formula or trigonometry for area calculation since the traditional height might not be directly measurable.
How do you find the area of an equilateral triangle?

+
For an equilateral triangle with side length 'a', the area can be calculated using the formula: (√3/4) × a2.
In closing, mastering the calculation of triangle areas is integral to understanding geometry. This guide has equipped you with tools ranging from basic to advanced methods for calculating triangle areas, alongside practical exercises. Through engaging in the suggested worksheets, you have the opportunity to reinforce your skills, ensuring proficiency in this crucial mathematical skill set. Continue exploring the depth of geometry, where each shape presents unique challenges and educational insights.



