5 Ways to Solve Area Regular Polygons Worksheet

Solving area problems for regular polygons is a common challenge in mathematics, often assigned in middle and high school geometry classes. Whether you're trying to master this topic for an upcoming test or just for the love of math, here are five comprehensive strategies to tackle regular polygon area problems effectively.
1. Master the Formula
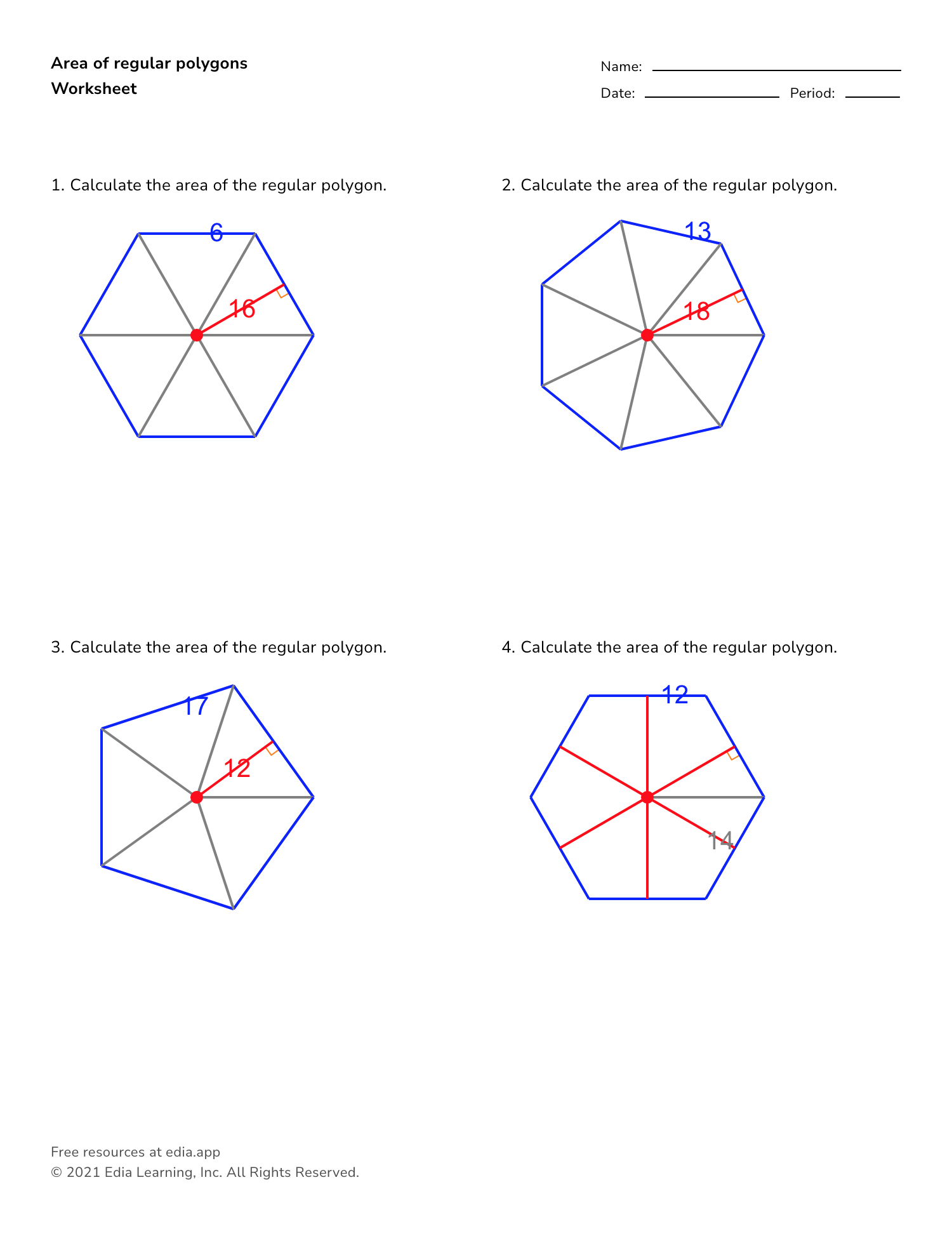
The most straightforward approach to solving area problems of regular polygons is by mastering the area formula for these shapes. Regular polygons, by definition, have equal sides and equal angles. Here is the basic formula for the area of a regular n-sided polygon:
- \[ \text{Area} = \frac{n \times s^2}{4 \times \tan\left(\frac{\pi}{n}\right)} \]
- where n is the number of sides.
- s is the side length.
Understanding how to use this formula:
- Identify the value of n and s from your problem statement.
- Calculate \tan\left(\frac{\pi}{n}\right), which will depend on the number of sides.
- Plug in these values to find the area.
Note that for some common polygons like squares, pentagons, and hexagons, there are simplified versions of this formula, but knowing the general formula allows for flexibility across different polygon types.
2. Use Division into Simple Shapes

Regular polygons can often be divided into simpler shapes:
- Equilateral triangles for a hexagon.
- Isosceles triangles or rectangles for other polygons.
Here’s how you might apply this method:
- Divide the polygon into a number of congruent triangles or rectangles.
- Calculate the area of one of these shapes and multiply by the number of segments.
| Polygon | Divide into... | Formula |
|---|---|---|
| Hexagon | 6 equilateral triangles | Area = \frac{3 \sqrt{3}}{2} \times s^2 |
| Pentagon | 5 isosceles triangles | Area = \frac{5 \times a^2 \times \sqrt{25 + 10 \sqrt{5}}}{4} |

⚠️ Note: This method simplifies calculations but can be complex for polygons with a high number of sides.
3. Leverage Coordinate Geometry
For regular polygons inscribed in a unit circle or any other circle:
- Plot the vertices of the polygon on a coordinate plane.
- Use coordinate geometry formulas to find the area using:
- Area of a triangle given vertices using determinants.
- Sum of areas of triangles that make up the polygon.
- Use sine and cosine rules to determine side lengths from angles.
- Calculate areas of constituent triangles using \text{Area} = \frac{1}{2}ab\sin(C) , where C is the included angle.
- If you know the apothem (a) and side length (s):
- Area = \frac{1}{2} \times n \times s \times a
- Graphing calculators like TI-84 can solve areas for polygons.
- Online geometric calculators or apps can provide quick solutions.
- Software like GeoGebra allows for visualization and area calculation.
- Mastering the formula directly applies to all regular polygons.
- Dividing into simpler shapes helps visualize and break down the problem.
- Coordinate geometry provides a systematic approach for polygons inscribed in circles.
- Trigonometry leverages known angles or chord lengths to find areas.
- Using software tools can simplify and speed up the process, especially for more complex polygons.
4. Apply Trigonometric Formulas
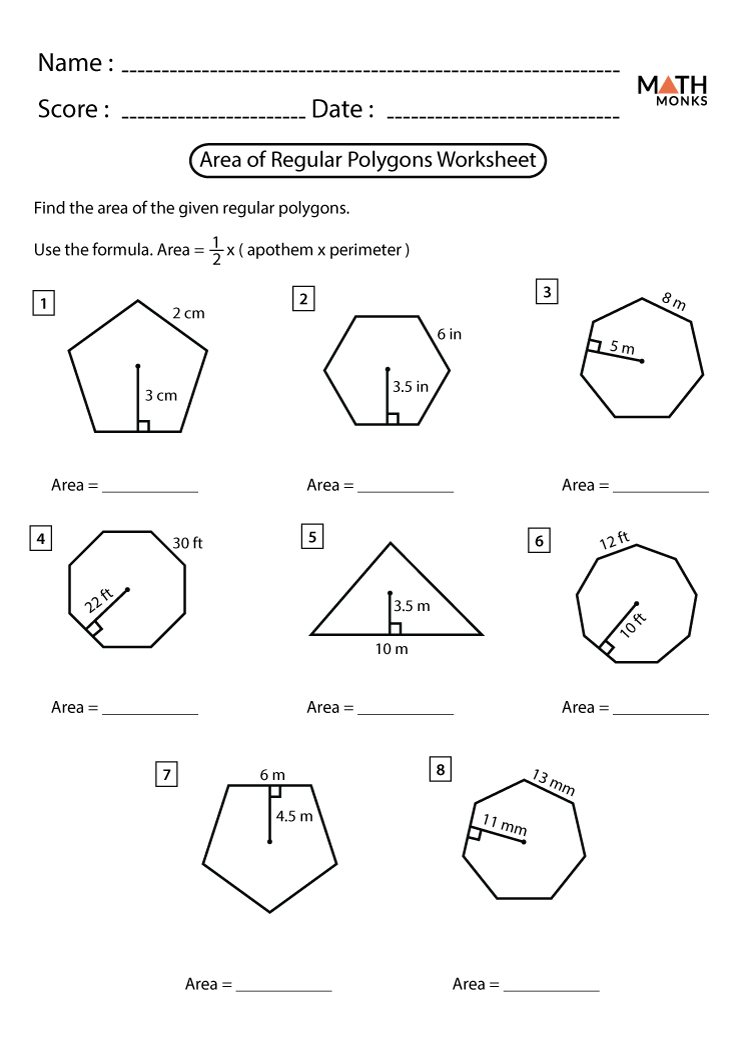
If you're dealing with polygons where you have angles or chord lengths rather than side lengths, trigonometry can be your best tool:
Here's an example for a pentagon:
5. Utilize Software Tools and Calculators

In today's digital age, using technology can be an excellent way to solve complex math problems, including polygon areas:
To summarize, whether you're finding the area of regular polygons for homework, exams, or just for fun, these five methods offer different perspectives and techniques:
Each method has its strengths, and sometimes a combination of strategies might be the best approach depending on the problem at hand.
What is the difference between a regular polygon and any polygon?

+
A regular polygon has all sides and angles equal, while any polygon might not have this symmetry. Regular polygons include shapes like equilateral triangles, squares, pentagons, etc., where all sides and angles are identical.
Why do we need different methods to find the area of regular polygons?

+
Different methods cater to different types of information provided in a problem. For example, if you have the side length, the direct formula is efficient. If you only know angles, trigonometric methods might be necessary.
Can I use these methods for non-regular polygons?

+
Yes, some methods like division into simpler shapes or coordinate geometry can work for non-regular polygons, but they might not yield a simple formula as with regular polygons.
What are common mistakes in calculating polygon areas?

+
Common errors include misidentifying the type of polygon, forgetting to account for the number of sides correctly, or incorrectly using trigonometric identities or coordinate geometry formulas.



