Pythagorean Theorem Worksheet: Free Answer Key Included

Mathematics is a fascinating subject that offers insights into the patterns and structures of the world around us. Among its many branches, geometry stands out for its visual appeal and practical applications. In this blog post, we delve into one of the fundamental principles of geometry: the Pythagorean Theorem. This theorem, known for its simplicity and beauty, states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Here, we'll explore how you can work with this theorem through a tailored worksheet, complete with an answer key to verify your solutions.
Understanding the Pythagorean Theorem

Before we dive into practical applications, let’s ensure we understand the theorem itself. The Pythagorean Theorem is mathematically expressed as:
- a² + b² = c², where a and b are the lengths of the two shorter sides (legs) of the right triangle, and c is the length of the hypotenuse.
This relationship holds true for all right triangles, making it a cornerstone in solving geometric problems involving distances and angles.

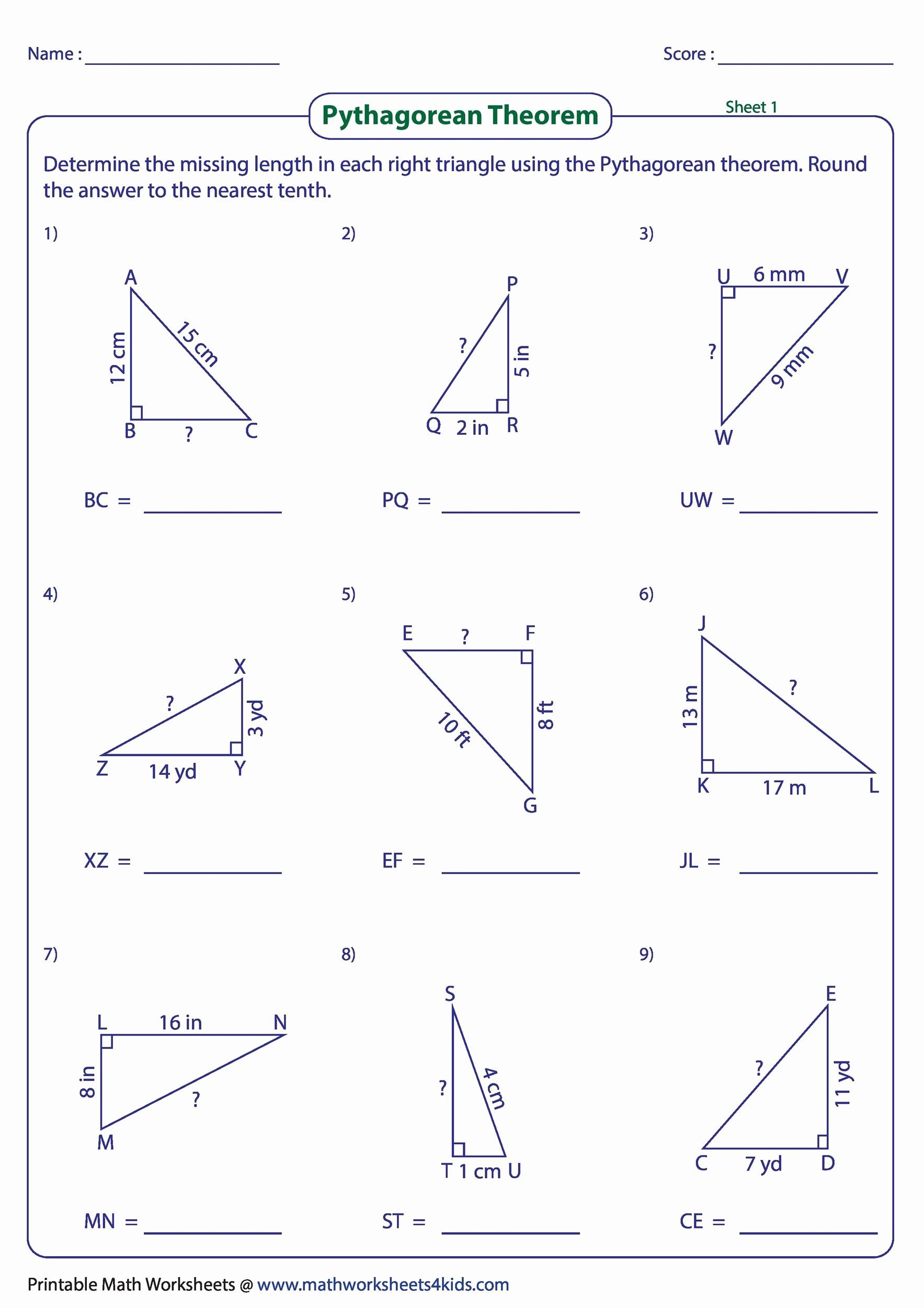
Pythagorean Theorem Worksheet

Now, let’s engage with the Pythagorean Theorem through a set of problems. Here’s a worksheet designed to help you practice applying this theorem:
| Problem | Given | Find |
|---|---|---|
| 1 | a = 3, b = 4 | c |
| 2 | a = 6, c = 10 | b |
| 3 | a = 5, c = 13 | b |
| 4 | b = 8, c = 17 | a |

Let's solve these problems step-by-step:
Solving Problem 1: Finding the Hypotenuse

Given: a = 3, b = 4
- Calculate: a² + b² = 3² + 4² = 9 + 16 = 25.
- Therefore, c = √25 = 5.
Solving Problem 2: Finding One Leg

Given: a = 6, c = 10
- Formulate: a² + b² = c².
- Substitute: 6² + b² = 10².
- Solve for b: 36 + b² = 100, thus b² = 100 - 36 = 64, which gives b = √64 = 8.
Solving Problem 3: Finding One Leg

Given: a = 5, c = 13
- Formulate: a² + b² = c².
- Substitute: 5² + b² = 13².
- Solve for b: 25 + b² = 169, thus b² = 169 - 25 = 144, which gives b = √144 = 12.
Solving Problem 4: Finding the Other Leg
Given: b = 8, c = 17
- Formulate: a² + b² = c².
- Substitute: a² + 8² = 17².
- Solve for a: a² + 64 = 289, thus a² = 289 - 64 = 225, which gives a = √225 = 15.
📝 Note: Remember to verify your calculations with the Pythagorean theorem formula to ensure accuracy. Always check whether your answer satisfies the relationship a² + b² = c².
Applications of the Pythagorean Theorem

Beyond basic geometry, the Pythagorean Theorem has practical applications:
- Construction and Architecture: For leveling, laying out foundations, and ensuring right angles.
- Navigation: To find distances between points on a map or in GPS coordinates.
- Computer Graphics: For rendering three-dimensional objects in two-dimensional space.
Recapitulation

In summary, we’ve explored the Pythagorean Theorem, from its basic statement to its application in solving problems via a worksheet. Here are the key takeaways:
- The Pythagorean Theorem is integral for solving problems involving right triangles.
- Practical problems can be approached step-by-step using the theorem’s formula.
- Verification through the theorem’s equation is essential for accuracy.
- This theorem has numerous real-world applications in various fields.
What is the Pythagorean Theorem?

+
The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This relationship is mathematically represented as a² + b² = c², where a and b are the legs and c is the hypotenuse.
Why is it important to check the solution with the Pythagorean Theorem?

+
Checking your solution with the Pythagorean Theorem ensures that your calculations are accurate. If your values do not hold true for a² + b² = c², there’s likely an error in your math. This verification step confirms the integrity of your solution, especially important in applications where accuracy is critical.
Can the Pythagorean Theorem be used for shapes other than right triangles?

+
The theorem is specifically for right triangles. However, principles derived from the Pythagorean Theorem can be adapted for use in other polygons or in three-dimensional space, but these are extensions rather than direct applications of the theorem itself.