Master Triangles: Discover Areas with Our Fun Worksheet

Triangles are fascinating geometric shapes that have intrigued humans since the dawn of civilization. They appear in ancient architecture, astronomy, art, and even in modern applications like engineering and computer graphics. Understanding how to calculate the area of a triangle is not only a fundamental skill in mathematics but also a practical tool in many professions. Today, we'll explore the concept of triangle areas with an engaging worksheet that will help you grasp this important skill. Whether you are a student, a teacher, or simply someone interested in geometry, this guide will provide you with insights, methods, and fun activities to learn about triangle areas effectively.
The Basics of Triangles


Before delving into the calculation of areas, let’s recap some fundamental properties of triangles:
- Vertices: Triangles have three vertices or points.
- Sides: Triangles are formed by three sides that connect the vertices.
- Angles: The sum of the internal angles in any triangle is always 180 degrees.
- Types: Triangles can be classified based on sides (equilateral, isosceles, scalene) or angles (acute, right, obtuse).
Calculating the Area of a Triangle
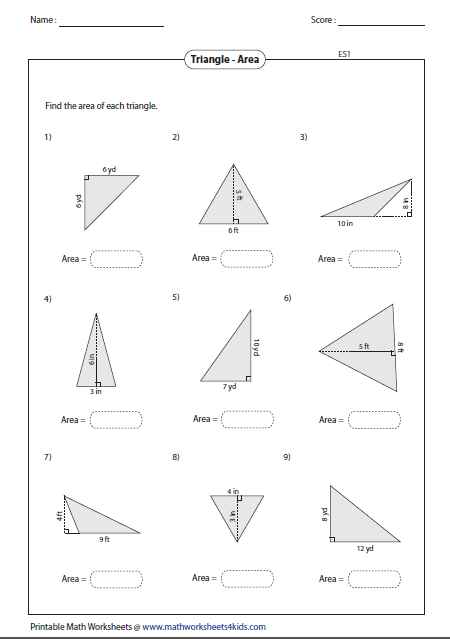
The most common formula for the area of a triangle is:
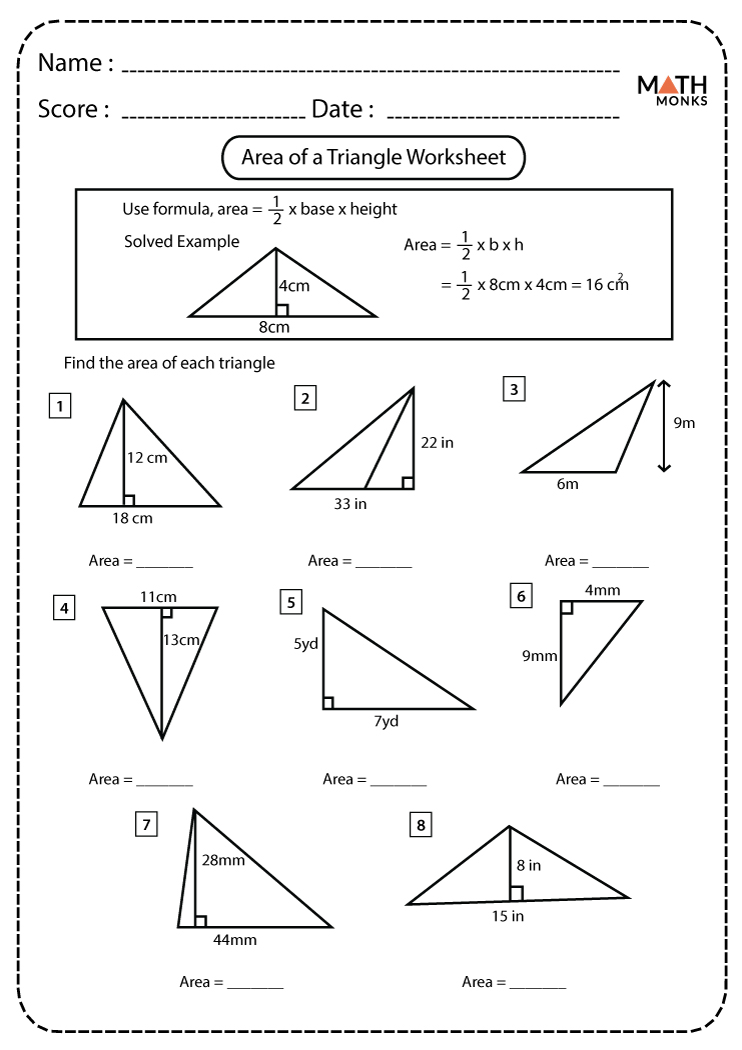
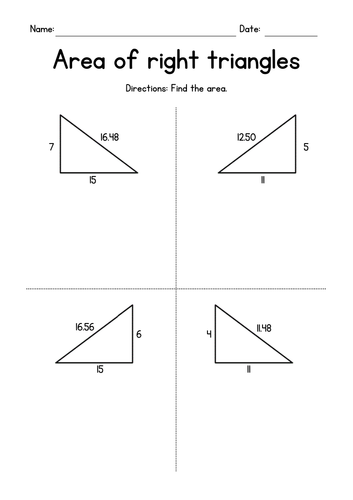
Area = ½ * Base * Height
This formula applies to any triangle. Here, the “base” is one side of the triangle, and the “height” is the perpendicular distance from the base to the opposite vertex.
Types of Triangles and Their Area Formulas

- Equilateral Triangle:
Area = (√3/4) * side² - Isosceles Triangle: If the legs are a and the base is b, the height can be derived, but let’s use the general formula:
- Right Triangle: If sides forming the right angle are a and b,
Area = ½ * a * b - Scalene Triangle: Here, the formula can be complex, often using Heron’s formula:
Area = √[s*(s-a)(s-b)(s-c)], where s is the semi-perimeter, and a, b, and c are the sides.
Our Fun Worksheet


Our triangle worksheet is designed to be both educational and enjoyable. Here’s what you’ll find in it:
- Calculating Areas: Problems where you calculate the area using different methods.
- Type Identification: Identify triangles by their sides or angles.
- Word Problems: Real-world scenarios where triangle area calculations are applied.
- Interactive Elements: Games or puzzles that challenge your understanding of triangle areas.
How to Use the Worksheet
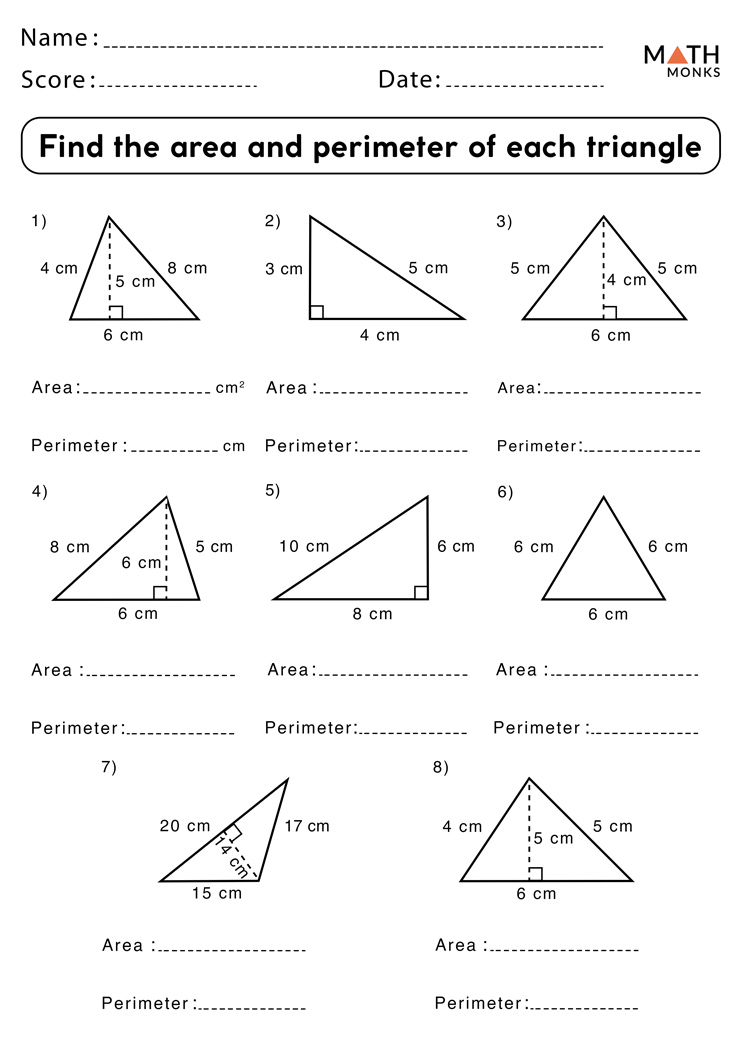
The worksheet comes with:
- Clear instructions for each section.
- Worked examples to guide you through the calculations.
- Plenty of space for problem-solving.
- A scoring system for self-assessment.
✨ Note: Use a ruler or straightedge to draw triangles accurately. It'll make your calculations more precise.
Practical Applications
Triangles are not just an abstract concept; they’re applied in various fields:
- Construction: Understanding the stability of triangular structures in architecture.
- Surveying: Determining land areas using triangulation.
- Design and Art: Creating compositions based on geometric shapes.
- Physics: Calculating forces in statics using triangle geometry.
Advanced Techniques
Once you master the basics, you can explore:
- Heron’s Formula: For any triangle when all side lengths are known.
- Trigonometry: Using trigonometric functions to find the height or area.
- Coordinate Geometry: Calculating areas using coordinates of the vertices.
Recap and Key Points

In this blog, we’ve explored how to calculate the area of various types of triangles, provided you with a fun worksheet to practice these calculations, and discussed practical applications of triangles. Here are the key takeaways:
- Triangles are classified by sides and angles, influencing how their areas are calculated.
- The base-height formula is universally applicable, but specialized formulas exist for different triangle types.
- Practical applications of triangle area calculations are vast, from architecture to engineering.
- Our worksheet helps you to practice and reinforce your understanding of triangle areas in an interactive way.
As you engage with triangles, remember that mastering these concepts opens up a world of problem-solving and real-world application. Keep practicing, and soon you'll find that triangles are not just figures on a page but powerful tools for understanding our world.
Can the area of a triangle ever be negative?
+
No, the area of a triangle can never be negative. It’s a scalar value that represents the space enclosed by the triangle, and it’s always positive or zero.
How can I verify my calculations for triangle areas?

+
You can cross-check your results using different formulas or methods like Heron’s formula or by physically measuring the area with a grid or by dividing the triangle into simpler shapes.
Why are triangles so common in architecture?

+
Triangles are inherently stable due to their shape; any three points not on a straight line can form only one triangle, making it rigid and resistant to deformation, which is essential in structures.