Unlock the Answers: Regular Polygons Area Worksheet

The quest for understanding the intricacies of regular polygons can be quite an adventure. These shapes, marked by their uniform sides and angles, not only captivate mathematicians but also artists, architects, and hobbyists seeking balance and symmetry. This blog post aims to unlock the answers to calculating the area of various regular polygons, providing an engaging guide for anyone looking to deepen their mathematical toolkit or enhance their geometry knowledge.
What Are Regular Polygons?

Before diving into the calculations, let’s first grasp what regular polygons are. A regular polygon is a shape where all sides and angles are equal:
- Equilateral Triangle: 3 sides
- Square: 4 sides
- Pentagon: 5 sides
- Hexagon: 6 sides
- And so on…

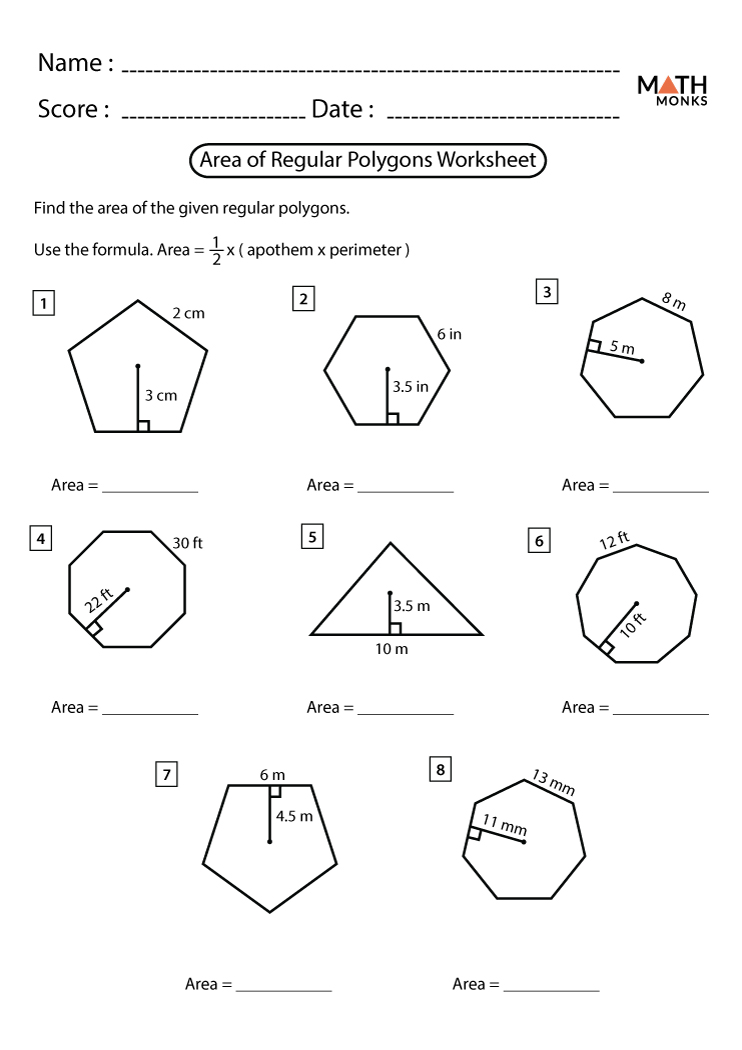
How to Calculate the Area of Regular Polygons

Each regular polygon has its own formula to compute its area, but they all share a common approach:
- Identify the number of sides (n)
- Determine the side length (s) or apothem (a)
- Apply the appropriate formula for the given polygon
Equilateral Triangle
For an equilateral triangle, the formula is simple:
Area = (√3/4) * s2
🔍 Note: The apothem for an equilateral triangle is √3/6 of its side length.
Square

The area of a square is one of the most straightforward:
Area = s2
Pentagon

For a pentagon, the formula involves trigonometry:
Area = (1⁄4) * n * a2 * cot(π/n)
where n is the number of sides (5 in this case), and a is the apothem.
Hexagon

Hexagons, commonly seen in nature and architecture, are also quite manageable:
Area = (3√3/2) * s2
or
Area = 3 * a2 * tan(π/6)
General Formula for Regular Polygons

For any regular polygon, the area can be calculated using:
Area = (n * s2 * a) / 2
Table of Formulas

| Polygon | Number of Sides | Area Formula |
|---|---|---|
| Equilateral Triangle | 3 | (√3/4) * s2 |
| Square | 4 | s2 |
| Pentagon | 5 | (1⁄4) * n * a2 * cot(π/n) |
| Hexagon | 6 | (3√3/2) * s2 |

🛠 Note: Ensure you use the correct apothem and side length for accurate calculations.
Understanding the formulas behind the areas of regular polygons enables us not only to appreciate their geometric beauty but also to apply these principles in various fields like design, architecture, and even video game development where polygons are fundamental in creating realistic 3D models.
The exploration into regular polygons can extend beyond what’s covered here. Consider delving into:
- Other polygons like the octagon and dodecagon
- Advanced geometric transformations
- Practical applications in everyday life
What is the difference between a regular polygon and an irregular polygon?

+
A regular polygon has all sides and angles equal, whereas an irregular polygon has at least one side or angle different from the others.
Can you provide examples of regular polygons in real life?

+
Regular polygons are common in nature and design; for instance, bees build their hives using hexagons, while stop signs are octagonal, and coins are circular (a polygon with an infinite number of sides).
How can one memorize the formulas for regular polygons?

+
Memorizing can be aided by understanding the derivation of each formula, practicing calculations regularly, and visualizing the shapes and their components like side length and apothem.
In essence, the art of calculating the area of regular polygons opens a door to the appreciation of mathematical beauty, the wonder of nature’s patterns, and the seamless integration of geometry into various fields. Whether you’re designing a building, crafting intricate artwork, or simply solving a geometry puzzle, these shapes provide a solid foundation for creative and analytical thinking.
In this world of shapes and numbers, we’ve merely scratched the surface. This journey through the land of regular polygons not only enhances our mathematical prowess but also connects us with the intricate world around us. Through understanding these formulas, we unlock a treasure trove of insights, turning the abstract into something deeply tangible and beautiful.



