Worksheet
Area of Composite Figures Worksheet With Answers: Download Now!
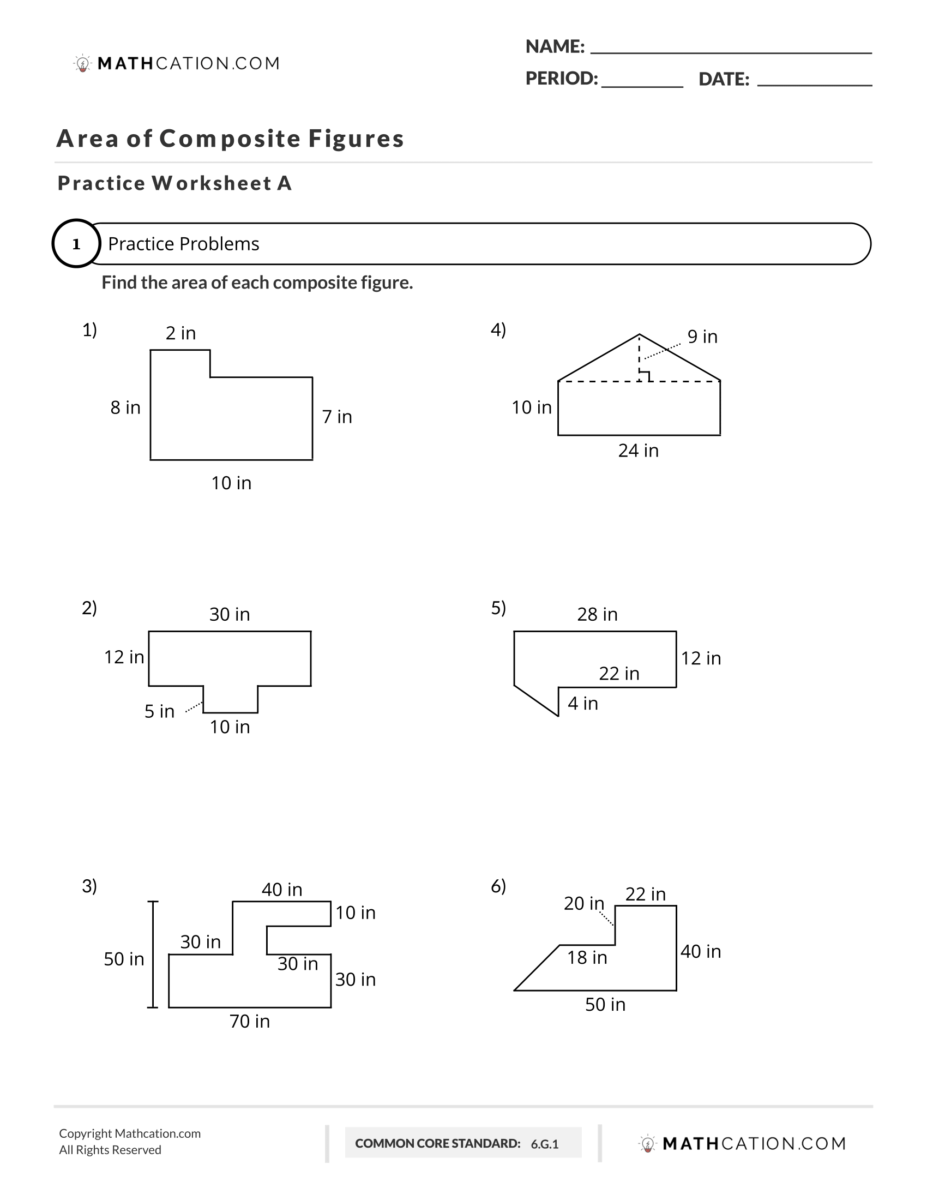
<p>Composite figures, often called compound shapes, are intriguing geometric objects made by combining two or more basic shapes. Understanding these figures is crucial for both students and professionals in various fields. From determining the volume of a complex building design to calculating the area of an irregular backyard for gardening, the application of composite figures is extensive. This blog post delves deep into the world of composite figures, providing not only a comprehensive guide to finding their areas but also offering you a printable worksheet complete with answers to practice your skills.</p>
<h2>The Basics of Composite Figures</h2>
<p>Before we jump into calculating areas, let's clarify what composite figures are:</p>
<ul>
<li>Composite figures consist of two or more simple shapes like rectangles, triangles, squares, and circles.</li>
<li>These shapes are combined in such a way that their boundaries might overlap or align.</li>
<li>Understanding how these shapes interact is key to finding the area of the whole figure.</li>
</ul>
<img src="composite-figure-example.jpg" alt="An example of a composite figure" />
<p>To approach a composite figure:</p>
<ul>
<li>Identify the individual shapes.</li>
<li>Calculate the area of each shape separately.</li>
<li>Add or subtract these areas as necessary to find the total area of the composite figure.</li>
</ul>
<h2>Calculating the Area of Composite Figures</h2>
<p>Here's a step-by-step process to calculate the area:</p>
<h3>Step 1: Break it Down</h3>
<ul>
<li>Divide the composite figure into its fundamental geometric shapes.</li>
<li>Label each shape for clarity.</li>
</ul>
<h3>Step 2: Find Individual Areas</h3>
<ul>
<li><b>For rectangles:</b> Area = Length × Width</li>
<li><b>For triangles:</b> Area = 0.5 × Base × Height</li>
<li><b>For circles:</b> Area = π × Radius<sup>2</sup></li>
</ul>
<h3>Step 3: Combine or Subtract Areas</h3>
<ul>
<li>If shapes overlap, subtract the overlapping area.</li>
<li>Sum up the areas of shapes where they align seamlessly.</li>
</ul>
<h3>Step 4: Verify</h3>
<ul>
<li>Check your calculations for accuracy. Are all units the same? Does the result make sense?</li>
</ul>
<p class="pro-note">✅ Note: When calculating areas, ensure all measurements are in the same unit. If not, convert them before computing the total area.</p>
<h2>Worksheet: Area of Composite Figures</h2>
<p>We've prepared a worksheet that challenges you to find the area of various composite figures. Here is a small sample:</p>
<table>
<tr>
<th>Figure</th>
<th>Shapes</th>
<th>Area</th>
</tr>
<tr>
<td><img src="composite-figure-1.jpg" alt="Composite Figure 1" /></td>
<td>
<ul>
<li>Triangle A: 4 cm base, 3 cm height</li>
<li>Rectangle B: 6 cm by 4 cm</li>
</ul>
</td>
<td>24 cm²</td>
</tr>
<tr>
<td><img src="composite-figure-2.jpg" alt="Composite Figure 2" /></td>
<td>
<ul>
<li>Rectangle C: 5 cm by 4 cm</li>
<li>Semicircle D: 2 cm radius</li>
</ul>
</td>
<td>Approx. 39.13 cm²</td>
</tr>
</table>
<p>Download the full worksheet to practice and enhance your skills:</p>
<p>Keep in mind:</p>
<ul>
<li>The formula for the area of a triangle (0.5 × Base × Height) assumes it's a right triangle or you know the base and height. For other triangles, you might need to use different formulas like Heron's formula.</li>
<li>Sometimes, you'll need to approximate areas for shapes like a quarter circle or a sector of a circle.</li>
</ul>
<p>To wrap it up, the area of composite figures is an essential skill for anyone working with or interested in geometry. It requires an understanding of basic shapes, their areas, and how they combine to form more complex structures. By practicing with worksheets and applying these principles in real-life scenarios, you'll find that mastering these skills can be both intellectually rewarding and practically useful. Whether you're designing, building, or simply learning, the knowledge of composite figures will enhance your ability to analyze and solve geometric problems.</p>
<div class="faq-section">
<div class="faq-container">
<div class="faq-item">
<div class="faq-question">
<h3>Why do I need to find the area of composite figures?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Understanding the area of composite figures is critical in fields like architecture, engineering, carpentry, and even in planning activities like landscaping. It allows you to estimate material needs, design layouts, and optimize space usage effectively.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>What if the shapes within the composite figure are not simple polygons?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Even if the shapes aren't simple polygons, you can still divide them into smaller, recognizable geometric shapes, use more advanced formulas like the shoelace theorem, or employ approximation methods like counting squares.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>Can I calculate the area of a composite figure without a worksheet?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Absolutely! The principles are the same. You can sketch the figure, identify its component shapes, calculate their areas, and combine them to find the total area. Worksheets are just tools for practice and to ensure your calculations are accurate.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>What are the common mistakes people make when calculating composite figure areas?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Common mistakes include forgetting to convert units, not accounting for overlapping areas, assuming shapes are simple when they aren't, and misidentifying shapes. Attention to detail and thorough checking can prevent these errors.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>How can I improve my skills in geometry, especially with composite figures?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Regular practice with worksheets, online problem sets, real-life applications, understanding the mathematical underpinnings of geometric formulas, and seeking out challenges will all help improve your skills with composite figures and geometry overall.</p>
</div>
</div>
</div>
</div>