5 Quick Math Transformations to Practice Today
Practicing math transformations can significantly enhance your problem-solving skills, making complex mathematical operations more intuitive. Transformations in mathematics refer to operations or functions applied to numbers, shapes, or equations to create new ones. Here are five essential transformations you should consider practicing today to sharpen your mathematical prowess:
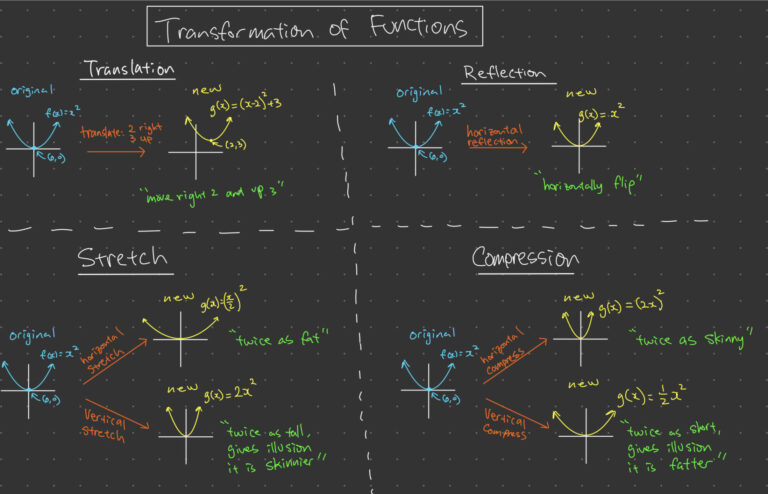
1. Translation


Translation is a fundamental transformation where every point of a shape or an equation is moved a fixed distance in a specified direction without altering its size or orientation. Here’s how you can practice:
- Graph simple shapes on a coordinate plane and translate them.
- Write equations in the form y = f(x) and shift them horizontally or vertically.
📐 Note: Translations do not change the shape or angle of the object, only its position.
2. Reflection


Reflection transforms a figure by flipping it over a line, known as the axis of reflection. You can practice this transformation by:
- Reflecting points or shapes across the x-axis, y-axis, or any line.
- Understanding how function graphs change under reflections, like y = -f(x) or y = f(-x).
3. Rotation


Rotation turns a shape around a point, known as the center of rotation, by a certain angle. To practice:
- Use geometric constructions or coordinate transformations to rotate figures.
- Understand the effect of rotations on functions, such as y = f(-x) rotated by 90 degrees.
4. Dilation


Dilation involves scaling a shape either larger or smaller without changing its shape. This transformation can be explored by:
- Scaling figures on a coordinate plane by a given factor.
- Transforming functions like y = f(ax) or y = kf(x) where a scales horizontally and k vertically.
🔍 Note: Dilation changes the size but maintains the shape of an object.
5. Function Composition
Function composition, while not a geometric transformation, plays a crucial role in understanding mathematical operations. It involves applying one function to the result of another function, symbolized as (g ∘ f)(x). Here’s how you can practice:
- Determine the domain and range of composite functions.
- Practice solving equations involving composite functions.
By integrating these transformations into your daily practice, you'll develop a deeper understanding of how mathematical objects can change and interact. This knowledge will not only make you adept at solving mathematical problems but also foster a creative approach to problem-solving.
Mathematics, at its core, is about recognizing patterns, understanding transformations, and seeing relationships in new ways. These practices will not only enhance your algebraic skills but also improve your spatial awareness and critical thinking abilities, which are invaluable in many areas of life and work.
What is the difference between translation and rotation in math?

+
Translation involves moving every point of a shape or graph a certain distance in a given direction without changing its shape, size, or orientation. Rotation, on the other hand, involves turning the shape around a point by a specified angle, which changes its orientation but not its size or shape.
How does dilation affect a graph?

+
Dilation affects a graph by changing the scale. If a graph is dilated horizontally, points are stretched or compressed along the x-axis. If dilated vertically, points move along the y-axis. This transformation changes the size of the graph but maintains its overall shape.
Can you explain function composition with an example?
+
Function composition is when you apply one function to the result of another. For example, if f(x) = x + 2 and g(x) = 3x, then (g ∘ f)(x) would be calculated as g(f(x)) = g(x + 2) = 3(x + 2) = 3x + 6.