5 Essential Tips for Solving Area of Composite Figures

When it comes to mathematical challenges in geometry, understanding how to calculate the area of composite figures ranks among the most intricate. These figures, made up of two or more simple geometric shapes, often leave students and professionals scratching their heads on where to begin. This in-depth guide will provide you with 5 essential tips for solving the area of composite figures, ensuring that you can approach these problems with confidence and accuracy.
Understanding Composite Figures

A composite figure can be imagined as a combination of simple geometric shapes such as rectangles, triangles, circles, or even trapezoids and pentagons. They arise in real-world applications from calculating the area of oddly-shaped land plots to designing unique architectural elements.
🔍 Note: Breaking down composite figures into familiar shapes is the foundation of solving these problems.
Tip 1: Break It Down
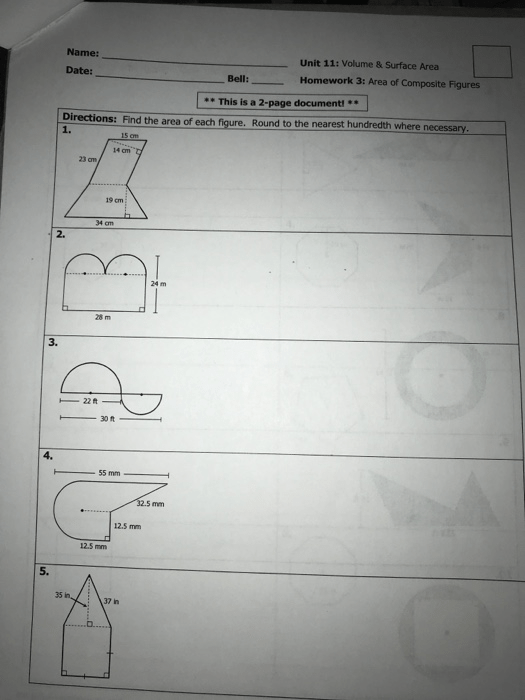
The key to mastering composite figure areas is to:
- Identify the basic shapes within the figure.
- Label all measurements and dimensions clearly.
- Calculate the area of each identified shape individually.
- Add or subtract these areas as necessary, depending on whether the shapes are overlapped or cut out.
📚 Note: Sometimes, it might be helpful to redraw the figure on grid paper to visualize the shapes more clearly.
Tip 2: Use Symmetry and Congruence

Many composite figures have symmetries or congruent parts which can be utilized to simplify your calculations:
- Look for congruent parts that can be treated as a single shape.
- Use symmetry to divide the figure into halves or mirror images, reducing the problem's complexity.
✨ Note: Recognizing symmetry can save you time and effort when calculating areas.
Tip 3: Apply Known Formulas

Once you've broken down the figure, you'll need to recall area formulas for each shape:
| Shape | Formula for Area |
|---|---|
| Rectangle | A = length × width |
| Triangle | A = ½(base × height) |
| Circle | A = πr² |
| Trapezoid | A = ½(a + b) × height |
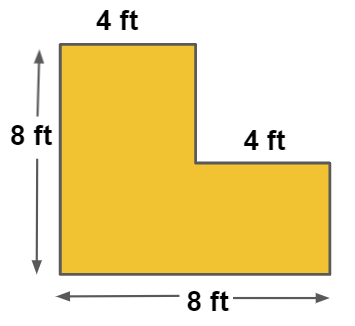
📐 Note: Remember, you might need to use the Pythagorean Theorem to find missing lengths for some shapes like triangles.
Tip 4: Address Overlaps and Subtractions

Some composite figures have parts that overlap or are subtracted from the total area:
- Identify overlapping areas or areas to be subtracted.
- Calculate these areas separately.
- Use the principle of inclusion-exclusion to add or subtract these areas to arrive at the composite figure's total area.
🧮 Note: This step requires careful attention to detail to ensure accuracy.
Tip 5: Utilize Additional Resources

If you're stumped on a particular composite figure:
- Consider using graph paper to visualize and estimate area visually.
- Make use of online area calculators or geometry software for complex shapes.
- Use real-life measurements and apply scale factors if necessary.
In conclusion, the ability to solve composite figures is a skill that blends spatial reasoning with algebraic techniques. By breaking down the figure, identifying symmetries, applying known formulas, addressing overlaps, and utilizing resources, you equip yourself with a powerful toolkit to tackle any geometry problem thrown your way. Remember, practice is the key to proficiency, and each problem solved adds to your understanding of these geometric enigmas.
What are the common shapes found in composite figures?
+
Common shapes include rectangles, squares, triangles (both right and non-right), circles, semi-circles, and various polygons like trapezoids and pentagons.
Can you find the area of an irregular composite figure?

+
Yes, by using the tips above, even irregular composite figures can be measured by breaking them down into simpler shapes, calculating each part’s area, and then combining or subtracting these areas as necessary.
How do I find the area if I don’t know all the side lengths?

+
If side lengths are missing, you might need to use geometric properties or theorems like the Pythagorean Theorem or apply scale factors if you have enough information to do so.



