Nets of 3D Shapes Worksheet: Engage and Learn Easily

Exploring the fascinating world of three-dimensional (3D) geometry is an essential part of any geometry curriculum. One of the most engaging ways to interact with 3D shapes is through the use of nets. Nets are flat patterns that can be folded to create 3D shapes, providing a hands-on learning experience that enhances understanding and retention. This worksheet aims to guide both teachers and students through the process of understanding, creating, and exploring nets of various 3D shapes.
Understanding the Basics of Nets

Nets provide a bridge between 2D and 3D worlds in mathematics. Here’s a quick overview:
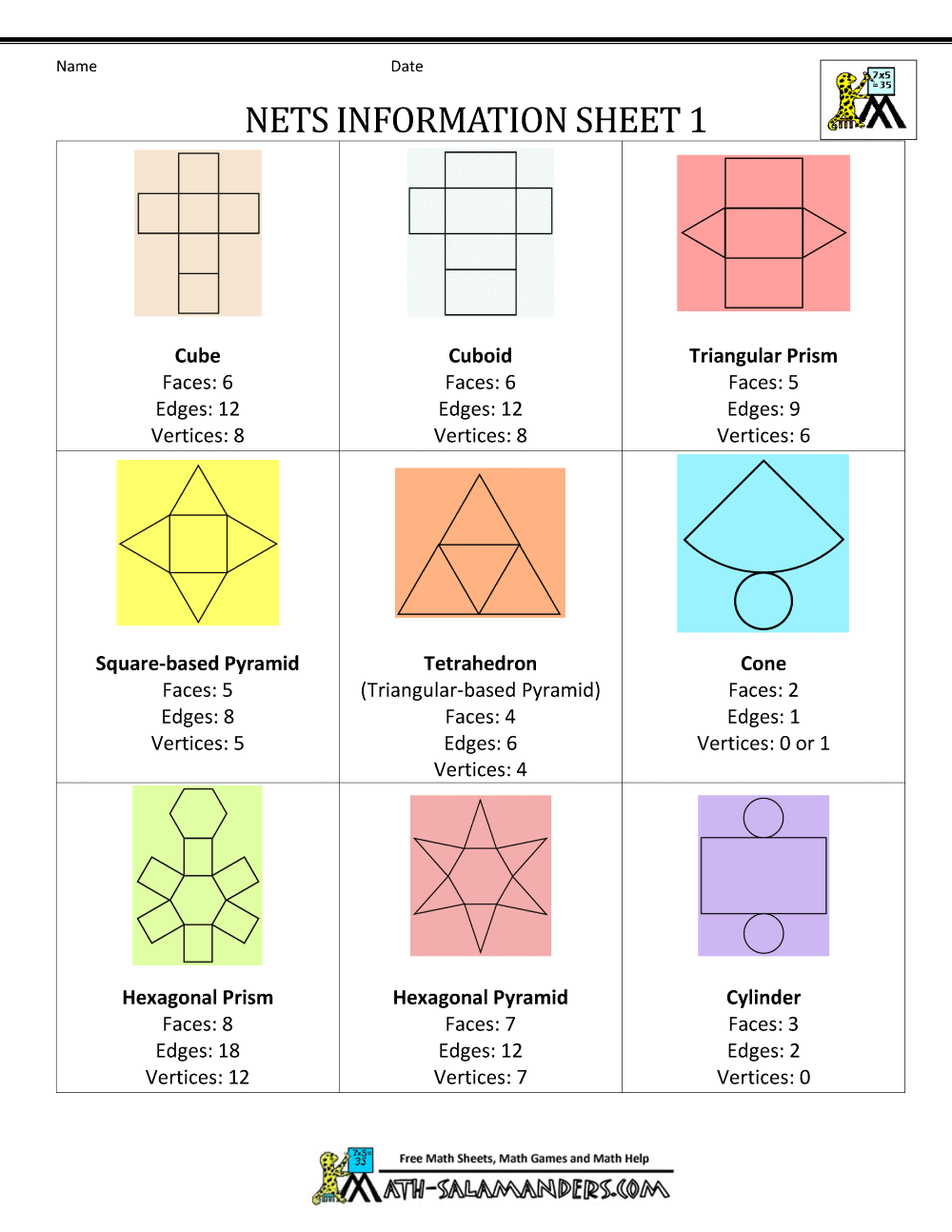
- Nets of Cube: A cube can be formed from six squares arranged in a cross pattern, with each square connected at edges.
- Nets of Cylinder: A rectangle for the body and two circles for the top and bottom, connected by the edges of the rectangle.
- Nets of Prism: Various shapes can form the faces of a prism, but at least two must be congruent.
- Nets of Pyramid: One base and triangular sides meeting at an apex.
Constructing and Visualizing Nets

Learning how to construct nets is fundamental for students. Here’s how you can engage in this process:
Step-by-Step Construction

- Select a 3D Shape: Choose a basic shape like a cube or a pyramid.
- Draw the Net: Use a ruler to ensure straight lines. For a cube, start with a central square, add four squares around it, and finish with one on top or bottom.
- Cut Out the Net: Carefully cut along the lines you’ve drawn. This is where precision matters.
- Fold: Crease the lines where faces should fold, and fold the net into the 3D shape.
- Secure: Use tape or glue to hold the shape together, though for educational purposes, practicing folding and unfolding is beneficial.
Practical Applications of Nets

The practical use of nets goes beyond academic exercises:
- Packaging and Manufacturing: Nets are used in product packaging design.
- Art and Design: Artists and designers utilize nets for 3D art projects and building structures.
- Architecture: Architects use nets to plan and visualize building layouts and elevations.
Interactive Net Creation

To make learning nets interactive:
Online Tools and Games

Here are some suggestions for engaging activities:
- NetNinja: A game where players must correctly piece together nets to form shapes before time runs out.
- Virtual Folding: Software allowing students to drag, fold, and explore virtual nets.
- 3D Net Puzzle: Physical puzzles that require fitting nets together in 3D space.
DIY Net Projects

Here are some DIY project ideas:
- Paper Models: From basic cubes to complex shapes like octahedrons, encourage students to build their own.
- Architectural Nets: Have students design simple buildings or rooms using nets.
Net Variations and Complex Shapes
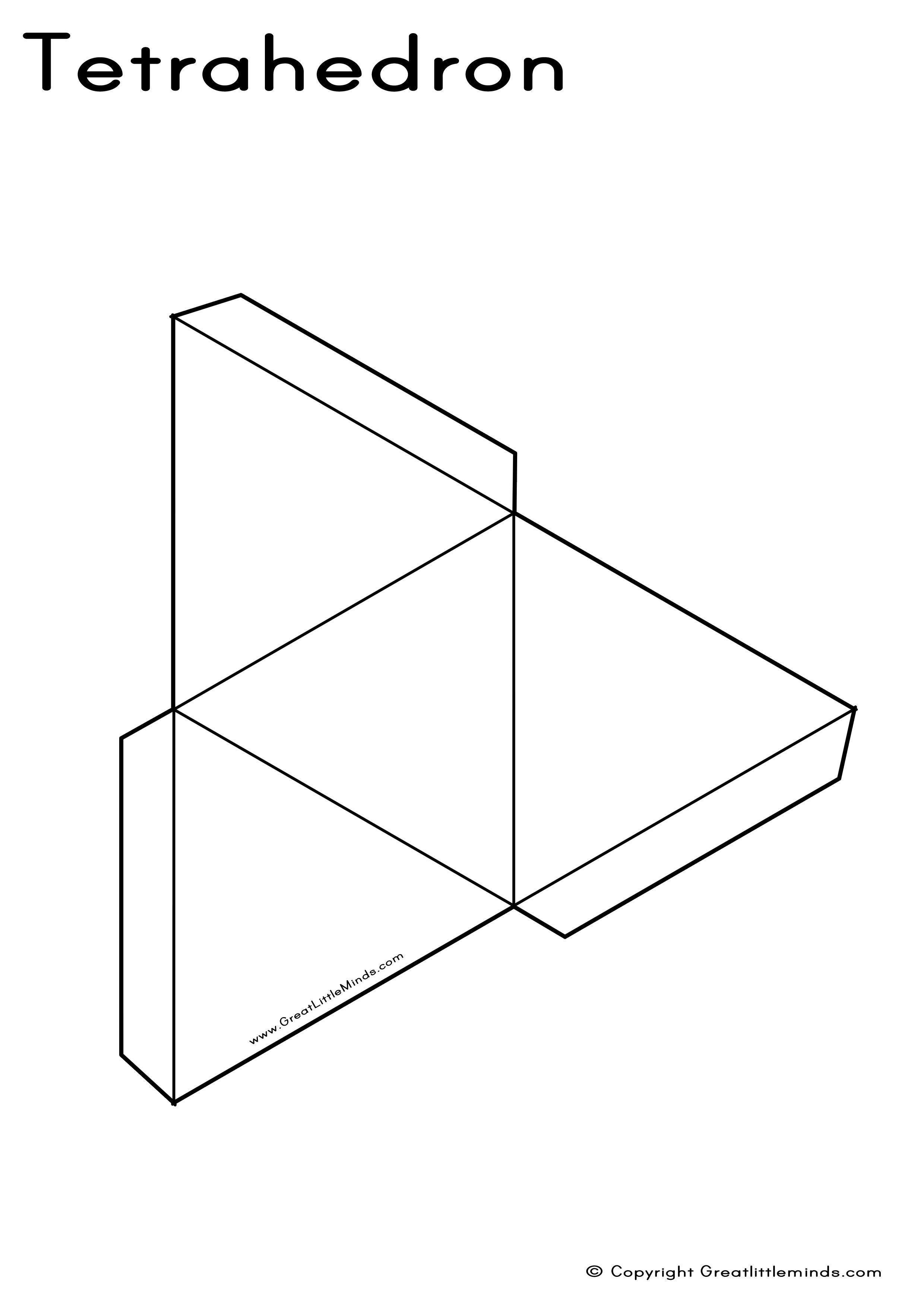
Going beyond basic shapes:
- Cylinders and Cones: These shapes have more than one correct net, allowing for discussions on design and efficiency.
- Irregular Polyhedrons: Introducing nets of shapes like icosahedrons or dodecahedrons can spark curiosity and challenge spatial reasoning.
💡 Note: While nets of basic shapes are straightforward, complex shapes might require multiple nets to fully understand their geometry.
Benefits of Using Nets in Education
Utilizing nets in education:
- Spatial Visualization: Nets help students visualize how flat shapes become three-dimensional.
- Pattern Recognition: Students learn to identify patterns in 3D shape construction.
- Problem Solving: Creating nets involves logical sequencing and problem-solving.
Engaging with nets provides a tactile, visual, and analytical learning experience, transforming abstract 3D shapes into something tangible and fun to explore. This hands-on approach not only aids in grasping the complexities of geometry but also fosters a deeper appreciation for spatial relationships, design, and even art. Through interactive activities, students can better understand the transition from 2D to 3D, enhance their problem-solving skills, and ignite their creative thinking. Nets, therefore, serve as an invaluable tool in education, bridging the gap between mathematical theory and real-world application.
Why are nets important in learning geometry?

+
Nets help students understand how three-dimensional objects are formed from two-dimensional shapes, enhancing spatial awareness and geometric reasoning.
Can nets be used for any 3D shape?

+
Most 3D shapes can be represented by nets, though some shapes like spheres have infinitely many possible nets due to their continuous curvature.
How do you know if a net is correct for a shape?

+
A net is correct if it can be folded into a 3D shape without any overlapping parts, and all faces are properly aligned with the shape’s sides.