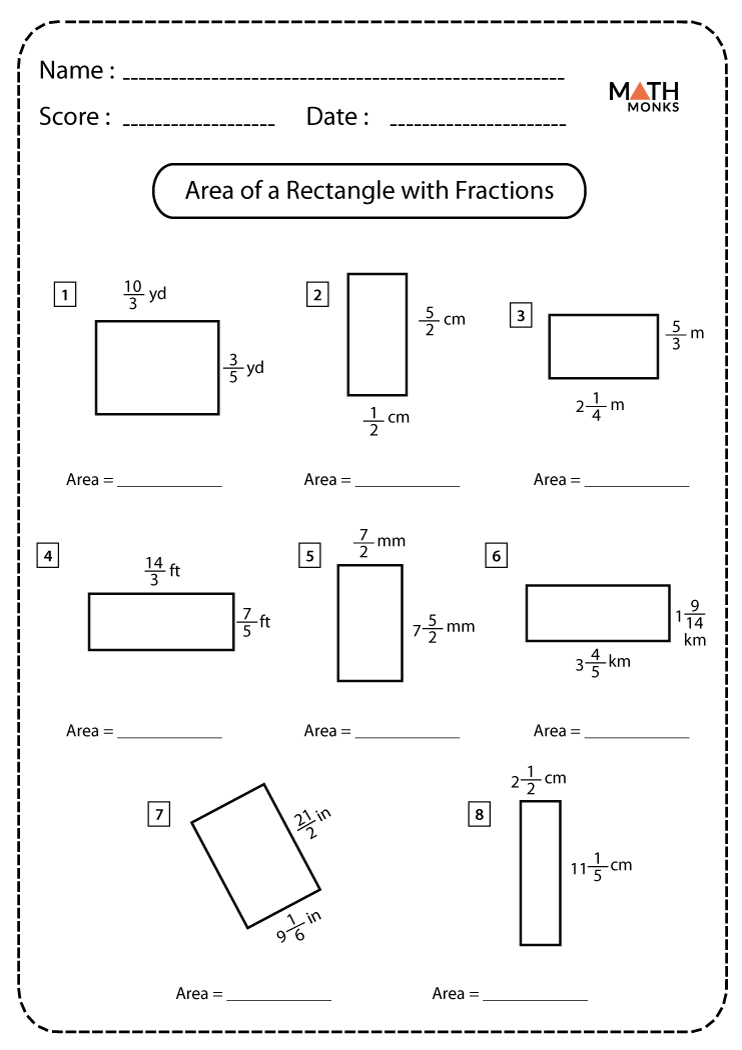
5 Tips to Solve Fraction Rectangle Area Problems Easily

If you've ever found yourself scratching your head over how to solve area problems in rectangles involving fractions, you're not alone. These problems can seem daunting at first glance, but with the right approach, they become manageable and even enjoyable. Here are five tips that will help you understand and solve these problems effortlessly:
Understand the Basics

Before diving into complex problems, make sure you understand the basics of fractions:
- The numerator represents how many parts you have.
- The denominator tells you how many parts the whole is divided into.
- To find the area of a rectangle, you multiply its length by its width.
Break Down the Problem

When dealing with fractions in rectangle area problems, breaking down the problem into simpler steps can be incredibly helpful:
- Identify the length and width. If they’re given as fractions, convert them to a common denominator.
- Multiply the fractions directly if they have common denominators. If not, adjust accordingly.
- Reduce the resulting fraction to its simplest form for your final answer.
📚 Note: Practice identifying the common denominators; it’s crucial for simplifying your calculations.
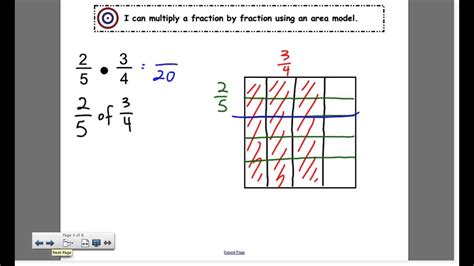
Use Visual Aids


Visualizing the problem can significantly aid in solving it:
- Draw the rectangle and divide it according to the given fractions.
- Understand the physical representation of what you’re calculating - this can help to correct any errors in your mental calculations.
- For example, if the problem states that a rectangle has a length of 3⁄4 and a width of 1⁄2, draw a rectangle and shade 3⁄4 of the length and 1⁄2 of the width.
Practice Converting Units
Converting units can sometimes make the problem simpler:
- Convert fractions to decimal forms or vice versa if it simplifies the problem.
- Knowing how to switch between different measurement units can also provide alternative perspectives or solutions to the problem.
🔍 Note: Be cautious when converting units to avoid loss of precision.
Use Real-World Examples

Relating abstract math problems to real-world scenarios can make them easier to solve:
- Think about common scenarios where fractions are used like in cooking or construction measurements.
- Ask yourself how the problem would be solved in real-life. This can often help in choosing the most logical approach.
Understanding rectangle area problems involving fractions is not just about the numbers but also about logical thinking and visual representation. By mastering these tips, you’ll be well-equipped to tackle these problems with confidence.
How do I know when to convert fractions to decimals?
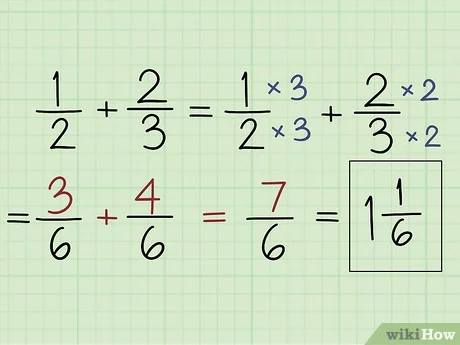
+
Convert to decimals when it simplifies the problem. If the calculations involve multiple fractions with differing denominators, decimals might be easier to handle.
What if my rectangle has fractional sides that are not similar?

+
Adjust the fractions to common denominators before multiplying or use the visual method to estimate the area.
Why do I need a common denominator to multiply fractions?

+
A common denominator simplifies the multiplication process, making it easier to work out the area without complicated conversions or corrections.



