5 Proven Methods for Solving Angles in Triangles
Triangles, one of the fundamental geometric shapes, provide a fascinating playground for mathematical enthusiasts, students, and professionals. Whether you're exploring the world of architecture, engineering, or pure mathematics, understanding the angles within triangles is essential. This article delves into five proven methods for solving angles in triangles, offering insights into both practical applications and theoretical underpinnings.
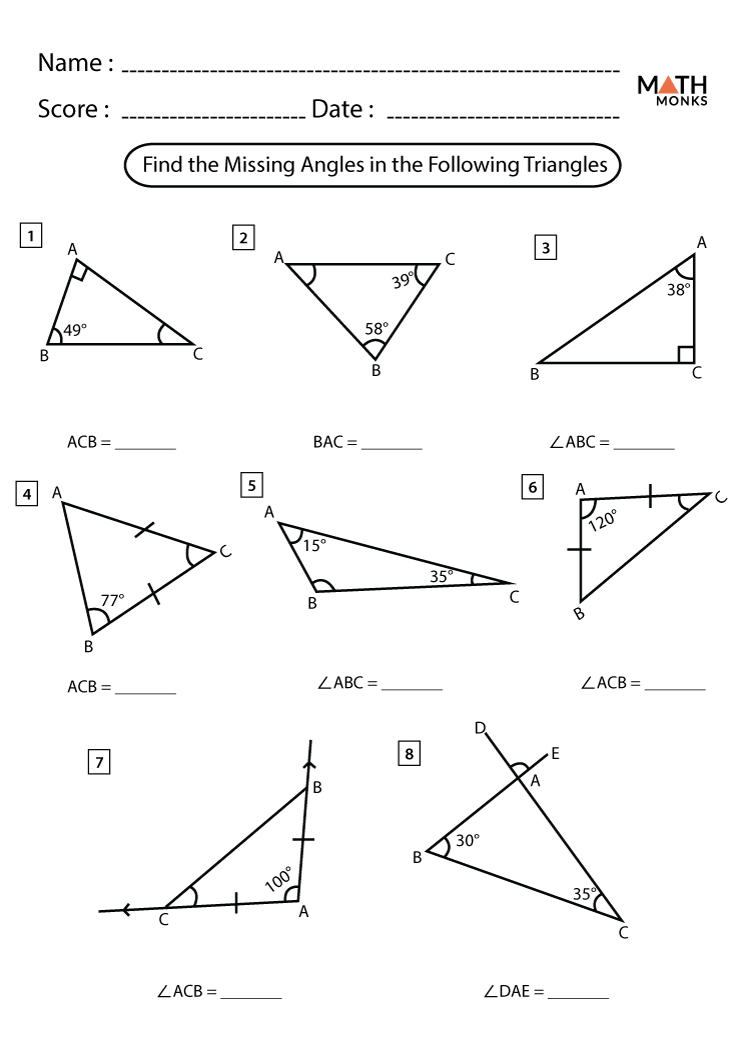
1. The Sum of Angles Theorem
The first and most basic rule when dealing with triangles is that the sum of the interior angles is always 180 degrees. This theorem, known as the Triangle Sum Theorem, allows you to solve for unknown angles by knowing at least two of the angles:
- If you know two angles, subtract their sum from 180° to find the third angle.
- Example: If a triangle has angles of 30° and 50°, the third angle is 180° - (30° + 50°) = 100°.
📝 Note: This theorem applies only to planar triangles, not to those on curved surfaces.
2. Exterior Angle Theorem

When we look at the exterior angle of a triangle, another handy property comes into play:
- The Exterior Angle Theorem states that an exterior angle is equal to the sum of the two non-adjacent interior angles.
- This can be particularly useful when only the exterior angle and one interior angle are known.
| Step | Description |
|---|---|
| 1 | Identify the exterior angle (Ex). |
| 2 | Know one interior angle (A). |
| 3 | Calculate the remaining interior angle: Ex = A + (180° - A) - 180° |

3. Law of Sines

The Law of Sines is an essential tool when dealing with angles and sides of any triangle:
- This law states that the ratio of the length of a side to the sine of the opposite angle is constant for all three sides of a triangle. Mathematically, it’s expressed as:
a/sin(A) = b/sin(B) = c/sin©
- Useful when you have:
- Two angles and any side
- Two sides and a non-included angle
📝 Note: The Law of Sines can lead to ambiguous cases where two solutions exist.
4. Law of Cosines

When the Law of Sines falls short, the Law of Cosines comes into play, particularly useful for solving triangles when:
- Three sides are known
- Two sides and the included angle are known
The formula for the Law of Cosines is:
c² = a² + b² - 2ab*cos©
📝 Note: This law can also be used for determining angles if all three sides are known.
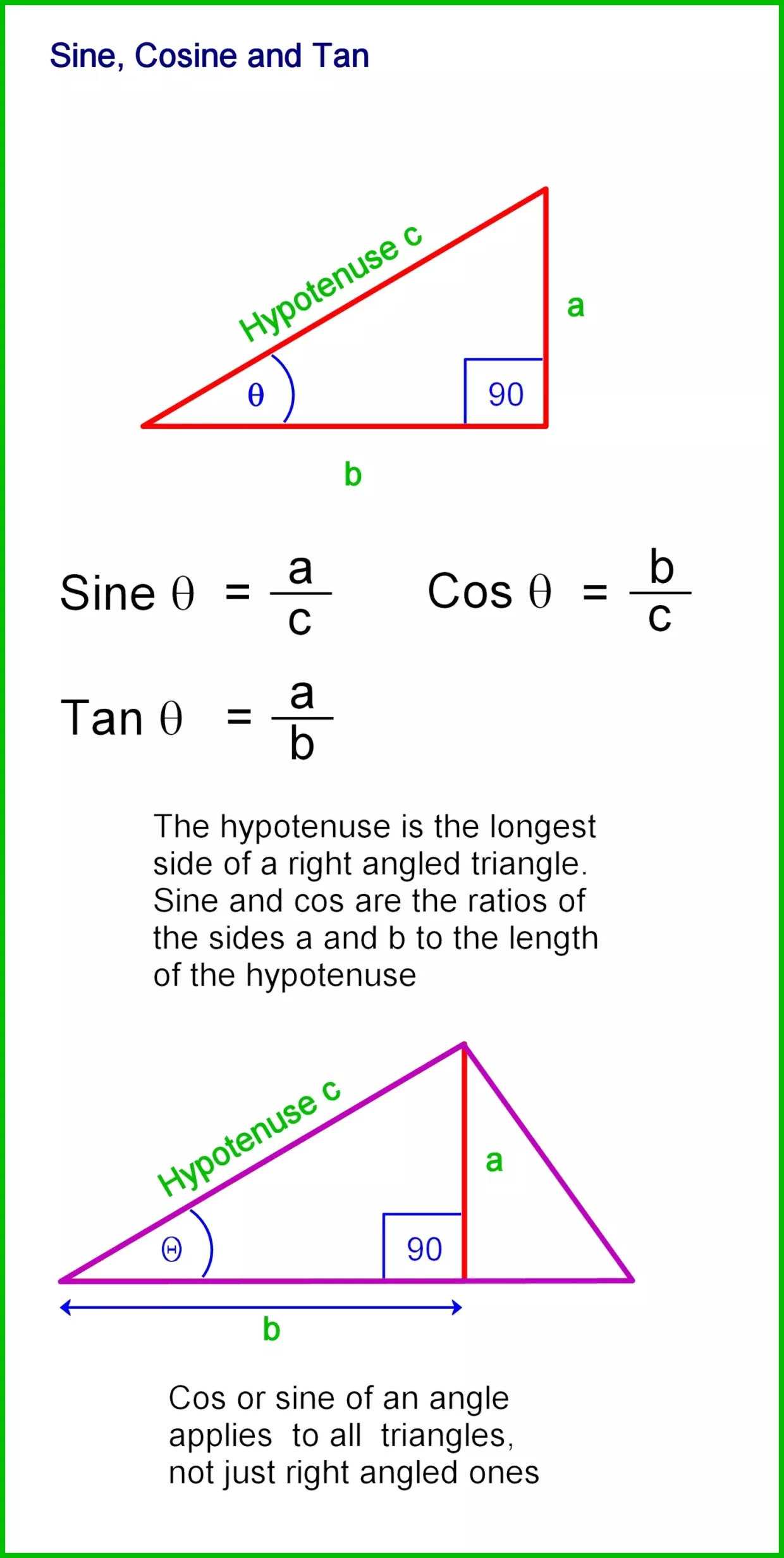
5. Trigonometric Identities and Ratios

While not exclusively a method for solving angles, using trigonometric identities can help when you have a mix of known angles and sides:
- Sine, Cosine, and Tangent identities can be used to solve angles:
- Example:
- If you know an angle and one side, use sin or cos to find another side, and then use the ratio to find another angle.
In conclusion, solving angles in triangles involves a mix of basic geometric theorems and more advanced trigonometric laws. From the straightforward Triangle Sum Theorem to the nuanced Law of Cosines, each method provides a unique toolset for different scenarios. Understanding these methods not only equips you with the ability to solve problems in geometry but also opens up a world of applications in real-world scenarios, from navigation to architecture and beyond. Whether you are navigating the classroom or the real world, these techniques are your key to mastering angles in triangles.
Why is the sum of the angles in a triangle 180°?

+
The sum of angles in a triangle equals 180° due to the parallel lines principle in Euclidean geometry. When a straight line intersects two parallel lines, the corresponding angles are equal, leading to the interior angles of a triangle summing up to 180°.
Can these methods be applied to non-right triangles?

+
Absolutely. While right triangles have certain properties due to the presence of a 90° angle, the methods discussed are universal for any type of triangle, whether acute, obtuse, or right.
How does the Law of Sines differ from the Law of Cosines?

+
The Law of Sines is used for solving triangles when angles and their opposite sides are known, while the Law of Cosines is more versatile and allows for solving when all sides or a combination of sides and an included angle are known.
Are there alternative methods to solve for angles?

+
Yes, other methods include using the circumcenter or incenter, orthocenter properties, or even applying calculus in more complex geometric problems.


