Mastering Angle Relationships Worksheet with Answers

Understanding Angle Relationships: A Comprehensive Guide
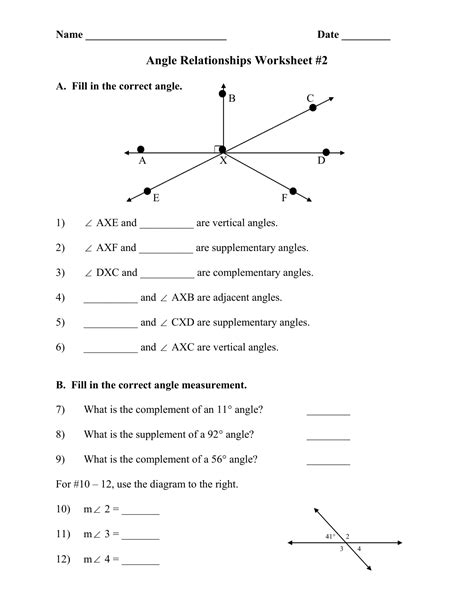
Angle relationships are a fundamental concept in geometry, and mastering them is essential for solving various mathematical problems. In this guide, we will delve into the world of angle relationships, exploring the different types, properties, and theorems that govern them. By the end of this article, you will be equipped with the knowledge and skills to tackle even the most complex angle relationship problems.
Types of Angle Relationships

Angles can be related in various ways, and understanding these relationships is crucial for solving mathematical problems. The following are some of the most common types of angle relationships:
- Complementary Angles: Two angles are complementary if their sum is 90 degrees. For example, if angle A measures 30 degrees, and angle B measures 60 degrees, then they are complementary.
- Supplementary Angles: Two angles are supplementary if their sum is 180 degrees. For example, if angle A measures 120 degrees, and angle B measures 60 degrees, then they are supplementary.
- Adjacent Angles: Two angles are adjacent if they share a common vertex and a common side. For example, if angle A and angle B share a common vertex and a common side, then they are adjacent.
- Vertical Angles: Two angles are vertical if they are formed by two intersecting lines and are opposite each other. For example, if angle A and angle B are formed by two intersecting lines and are opposite each other, then they are vertical.
Properties of Angle Relationships

Angle relationships have several properties that make them useful for solving mathematical problems. Some of the most important properties include:
- Angle Addition Postulate: The sum of the measures of two angles is equal to the measure of their sum. For example, if angle A measures 30 degrees, and angle B measures 60 degrees, then the sum of their measures is 90 degrees.
- Angle Subtraction Postulate: The difference of the measures of two angles is equal to the measure of their difference. For example, if angle A measures 120 degrees, and angle B measures 60 degrees, then the difference of their measures is 60 degrees.
- Complementary and Supplementary Properties: If two angles are complementary or supplementary, then their sum is equal to 90 or 180 degrees, respectively.
Theorems of Angle Relationships

There are several theorems that govern angle relationships, including:
- Complementary Angles Theorem: If two angles are complementary, then their sum is equal to 90 degrees.
- Supplementary Angles Theorem: If two angles are supplementary, then their sum is equal to 180 degrees.
- Vertical Angles Theorem: If two angles are vertical, then they are equal.
Worksheet with Answers

Now that we have explored the different types, properties, and theorems of angle relationships, it’s time to put your knowledge to the test. The following worksheet includes 10 problems that will help you master angle relationships.
| Problem | Answer |
|---|---|
| 1. If angle A measures 30 degrees, and angle B measures 60 degrees, are they complementary or supplementary? | Complementary |
| 2. If angle A measures 120 degrees, and angle B measures 60 degrees, are they complementary or supplementary? | Supplementary |
| 3. If two angles are adjacent and form a straight line, what is the sum of their measures? | 180 degrees |
| 4. If two angles are vertical, what is the relationship between their measures? | Equal |
| 5. If angle A measures 45 degrees, and angle B measures 45 degrees, what is the sum of their measures? | 90 degrees |
| 6. If angle A measures 120 degrees, and angle B measures 60 degrees, what is the difference of their measures? | 60 degrees |
| 7. If two angles are supplementary, what is the sum of their measures? | 180 degrees |
| 8. If two angles are complementary, what is the sum of their measures? | 90 degrees |
| 9. If angle A measures 30 degrees, and angle B measures 60 degrees, what is the sum of their measures? | 90 degrees |
| 10. If two angles are vertical, what is the relationship between their measures? | Equal |

Conclusion
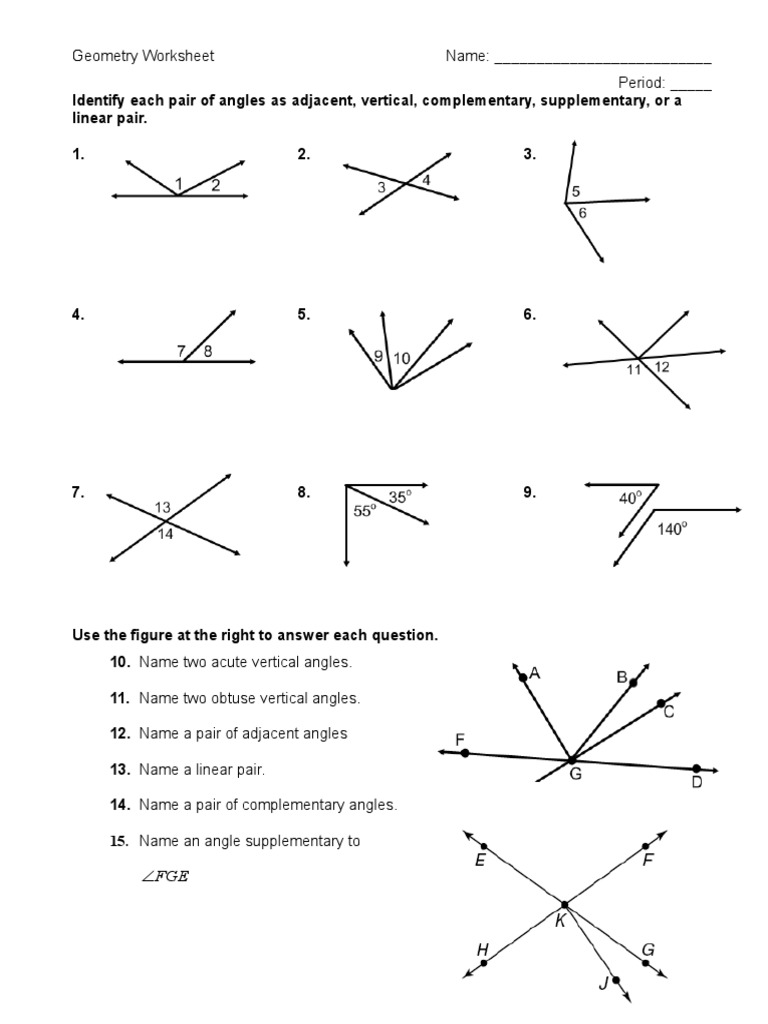
Mastering angle relationships is essential for solving various mathematical problems. By understanding the different types, properties, and theorems of angle relationships, you can tackle even the most complex problems with confidence. Remember to practice regularly and apply the concepts learned in this guide to real-world problems. With dedication and persistence, you will become proficient in angle relationships and be able to solve problems with ease.
What are the different types of angle relationships?

+
The different types of angle relationships include complementary angles, supplementary angles, adjacent angles, and vertical angles.
What is the sum of the measures of two complementary angles?

+
The sum of the measures of two complementary angles is 90 degrees.
What is the relationship between the measures of two vertical angles?

+
The measures of two vertical angles are equal.
Related Terms:
- Angle Relationships Worksheet PDF
- Angle pair Relationships worksheet
- angle relationships pdf
- angle relationships worksheet pdf
- kuta software supplementary angles
- angle pairs worksheet pdf



