5 Essential Tips for Solving Angle Proofs

In the realm of geometry, understanding and solving angle proofs can be a challenging yet rewarding endeavor. Angle proofs provide the foundation for much of geometry, from basic properties of triangles to complex theorems. Whether you're a student grappling with geometric theorems or an enthusiast diving deeper into the subject, mastering angle proofs can significantly enhance your mathematical prowess. Here are five essential tips to help you navigate through the complexities of angle proofs.
Understand Basic Concepts


Before diving into proofs, ensure you have a firm grasp on basic angle types and relationships. Key concepts include:
- Types of Angles: Acute, obtuse, right, straight, and reflex angles.
- Angle Relationships: Complementary, supplementary, adjacent, vertical, and linear pair angles.
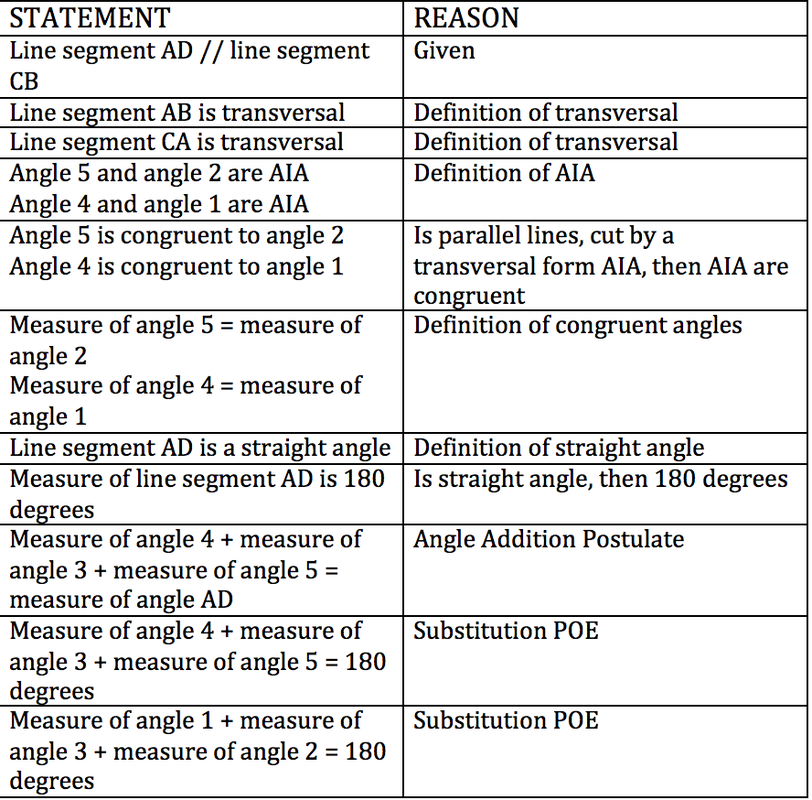
- Transversals: Understand how angles are formed when a transversal intersects parallel lines.
Use Visual Aids


Visual representation is key in geometry:
- Sketch diagrams to illustrate problems visually.
- Label all angles and relevant points clearly.
- Highlight or color-code different relationships for quick reference.
Apply Axioms and Postulates

| Postulates/Axioms | Description |
|---|---|
| Parallel Postulate | Through a point not on a given line, exactly one line can be drawn parallel to the given line. |
| Angle Addition Postulate | If point B lies in the interior of ∠AOC, then m∠AOB + m∠BOC = m∠AOC. |

Utilize these fundamental truths to build your arguments:
- Recognize when these can be directly applied.
- Remember that axioms are self-evident truths; they don’t require proof.
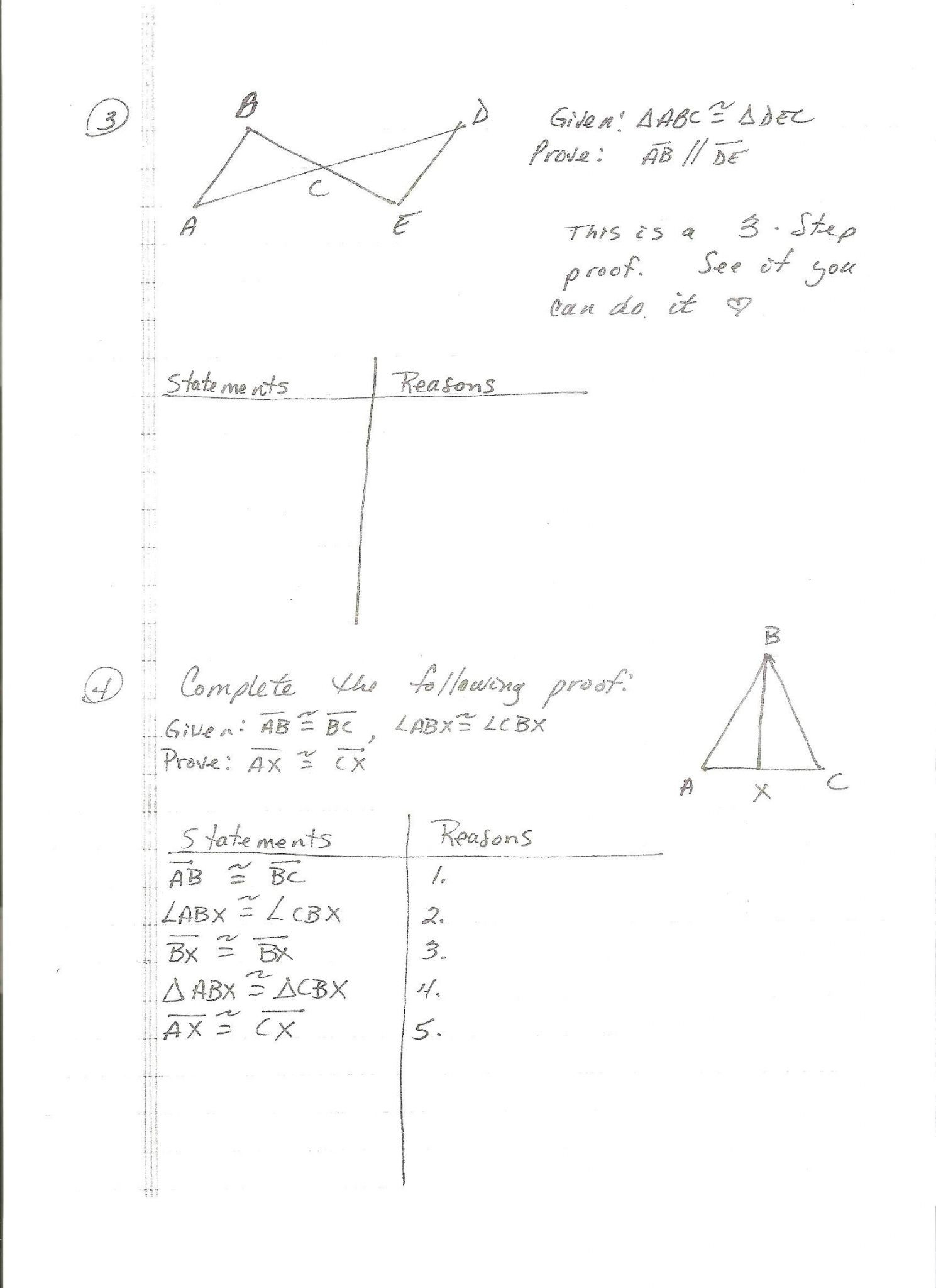
Prove Step by Step

Geometry proofs are sequential, much like a narrative:
- Start with what is given.
- Proceed with logical deductions.
- Employ definitions, properties, theorems, or axioms at each step.
- Use clear statements and justifications.
📝 Note: Be meticulous with every detail in your proof. An error at any step can lead to a false conclusion.
Practice Makes Perfect

Like any skill, proficiency in angle proofs comes from practice:
- Solve a variety of problems from textbooks or online resources.
- Join study groups or participate in forums for peer discussions.
- Reflect on your solutions, learning from mistakes, and understanding different approaches.
By consistently applying these tips, you will not only become adept at solving angle proofs but also develop a deeper understanding of geometric relationships. Geometry is a subject where visualization meets logical reasoning, and your ability to navigate through angles will enhance your overall grasp of the mathematical universe.
What are the basic types of angles in geometry?
+
The basic types of angles include acute (less than 90°), right (exactly 90°), obtuse (between 90° and 180°), straight (exactly 180°), and reflex (greater than 180°).
How can visual aids help in solving geometry proofs?
+
Visual aids like diagrams make it easier to see spatial relationships and visualize geometric properties, which can clarify the steps needed in a proof.
What is the importance of axioms in geometric proofs?

+
Axioms are the fundamental principles accepted without proof; they provide the starting point for deriving theorems, making them essential in constructing proofs.



