Master Alternate Interior Angles with Our Fun Worksheet

In the fascinating world of geometry, understanding angles and their relationships can be both a challenge and an opportunity for growth. When students dive into the topic of alternate interior angles, they encounter concepts that are essential not only for their mathematical education but also in solving real-world problems involving lines and shapes. Today, we'll explore this geometric principle through an engaging worksheet, designed to help learners of all ages master the art of identifying and calculating these angles with precision and confidence.
What Are Alternate Interior Angles?

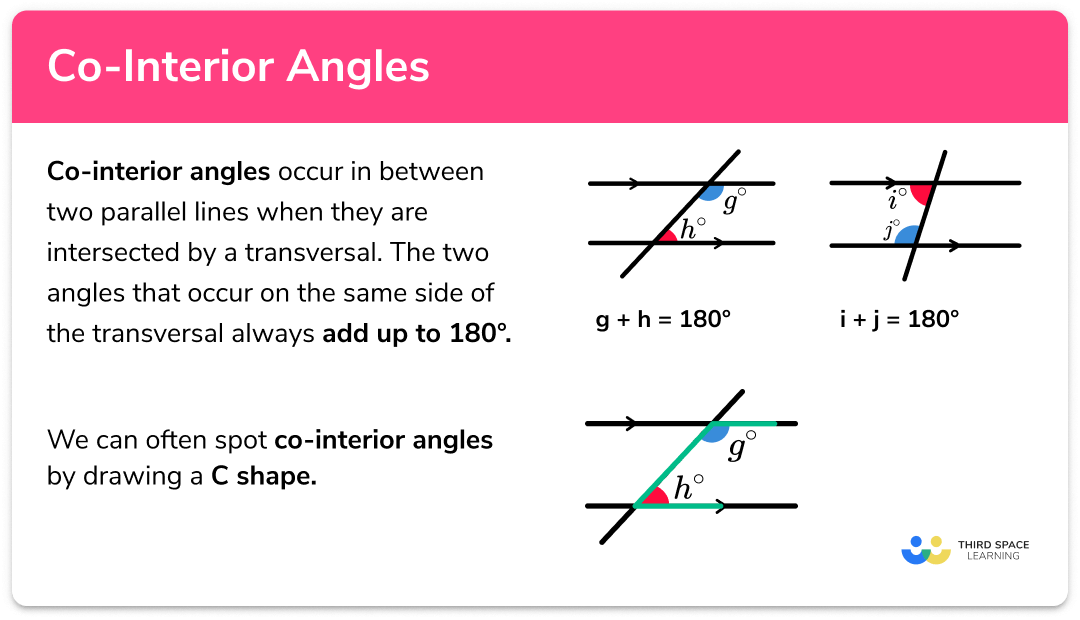
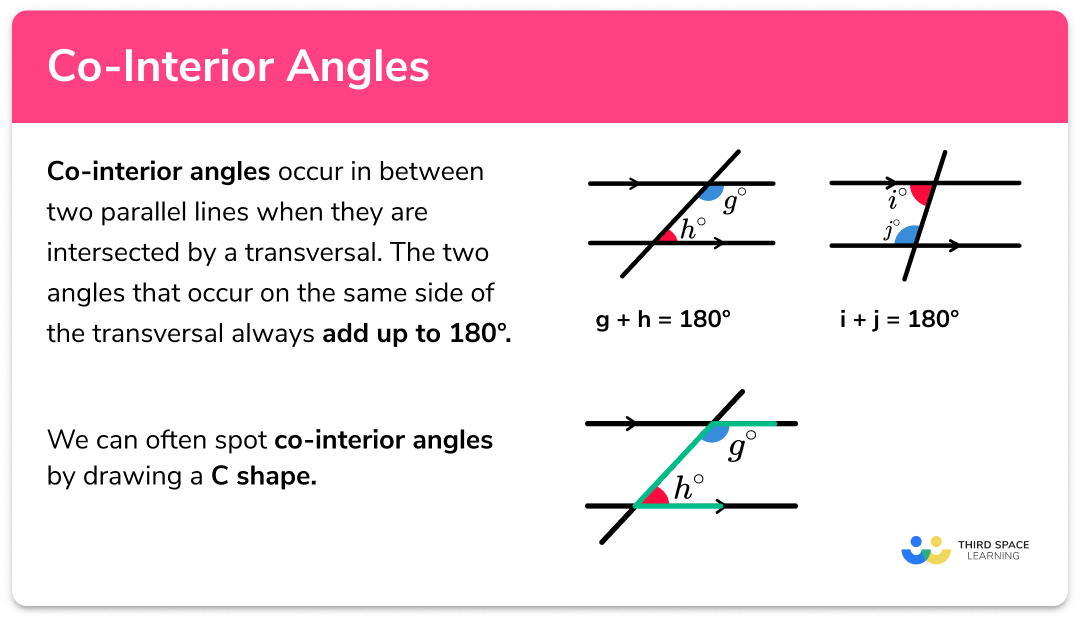
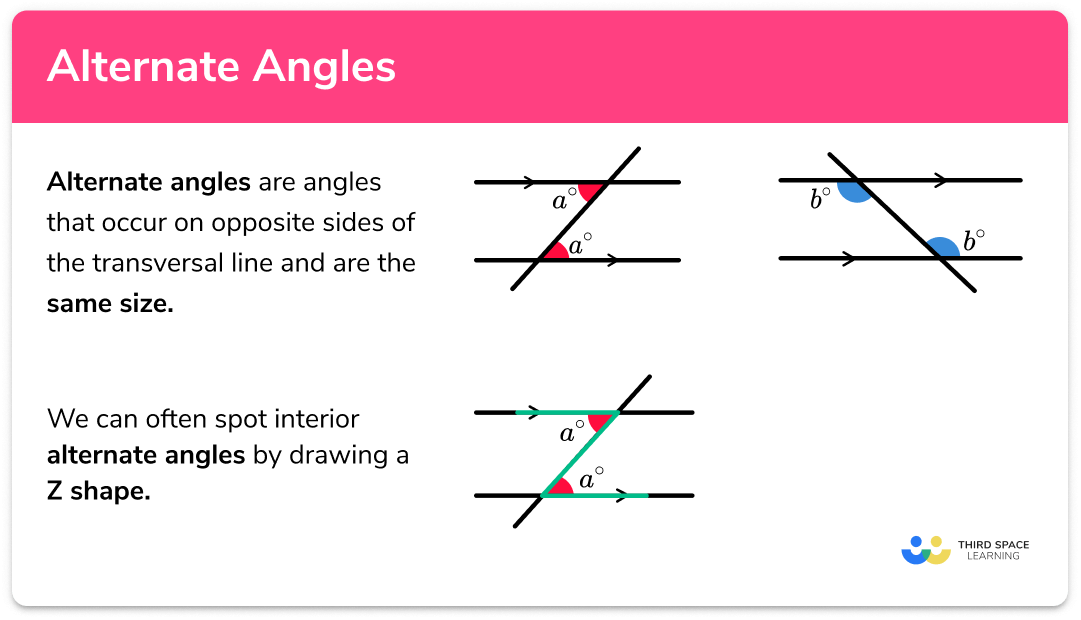
Before diving into our worksheet, let’s establish a clear understanding of what alternate interior angles are. These are pairs of angles found on opposite sides of the transversal but inside the two lines that the transversal intersects. They are:
- Opposite: They appear on opposite sides of the transversal.
- Interior: They are located within the two parallel lines, or as we’ll see in our worksheet, non-parallel lines as well.
- Alternate: One angle is found above the transversal while the other is below it.
These angles are congruent when the lines cut by the transversal are parallel, making them a crucial concept in geometric proofs and real-life applications like designing buildings or understanding optical illusions.
The Worksheet: A Journey Through Angles
Our worksheet is meticulously crafted to guide students through different exercises, progressively increasing in complexity. Here’s what to expect:
- Identification Exercises: Students start by recognizing alternate interior angles in diagrams, enhancing their visual-spatial intelligence.
- Calculation Problems: Next, they’re tasked with solving for unknown angles, which tests their algebraic and logical reasoning skills.
- Application: Real-life scenarios where students must find these angles, applying what they’ve learned in tangible situations.
- Proofs: Concluding with formal proofs to solidify the understanding that alternate interior angles are congruent in parallel lines situations.
Key Features of Our Worksheet

- Progression: Each section builds upon the last, ensuring a coherent learning experience.
- Visual Aids: Rich diagrams and illustrations to help visualize the concepts.
- Feedback Opportunities: Space for students to reflect on their work and receive feedback.
- Differentiation: Challenges are scalable, catering to various learning levels.
📝 Note: The worksheet includes hints and tips for self-assessment and provides extension activities for those who wish to delve deeper.
Engaging Students with Alternate Interior Angles
Engagement is key when mastering any concept, especially in math. Here are ways to make learning about alternate interior angles enjoyable:
- Real-World Connections: Link the angles to everyday life, like seeing them in road signs or architecture.
- Games and Competitions: Turn the identification and calculation of angles into a friendly competition or a game.
- Hands-On Activities: Use physical objects to physically create angles, making the abstract concept tangible.
- Artistic Expression: Allow students to create pieces of art or design patterns using these angles.
Throughout our journey, we've found that alternate interior angles are not just an academic concept but a tool for understanding the world around us. They appear in art, architecture, engineering, and beyond. The worksheet we've explored provides a comprehensive approach to mastering these angles:
- Through the identification exercises, learners become adept at spotting alternate interior angles in various scenarios.
- Calculation problems sharpen algebraic skills and logical thinking, pushing students to solve for unknown angles confidently.
- The application section bridges the gap between theory and practice, showing the real-world importance of these angles.
- Finally, the formal proofs solidify the understanding that when two lines are cut by a transversal and are parallel, alternate interior angles are congruent.
Our commitment to learning alternate interior angles is more than just mastering a part of geometry. It's about gaining a tool for problem-solving, understanding spatial relationships, and appreciating the mathematics that surrounds us. Whether you're designing a layout for a room, planning urban spaces, or simply appreciating the beauty of geometry in art, these angles play a fundamental role.
So, with your worksheet in hand and our fun exercises, you're now equipped to navigate the world of alternate interior angles with ease. Remember, as you delve into these angles, you're not just learning about math; you're exploring the patterns and structures that make our environment beautiful and functional. Keep practicing, keep questioning, and keep marveling at the world of angles, where the beauty of symmetry and the utility of calculation meet.
Why are alternate interior angles important?

+
Alternate interior angles are crucial in understanding the properties of parallel lines and transversals, which is fundamental in various mathematical proofs and real-world applications like engineering, architecture, and physics.
How do I remember which angles are alternate interior?
+
Remember that alternate interior angles are on opposite sides of the transversal, one above and one below, and they are inside the two lines being cut. If you think of the transversal as a line that “travels” across two lines, these angles are the ones that “alternate” from side to side within those lines.
Can you give an example of alternate interior angles in real life?
+
One common example is when you’re walking along a street with two parallel lanes. If you look at the angle where a side street intersects these lanes, the angles formed by this intersection and the parallel lanes are alternate interior angles.