5 Key Answers for Algebra 2 Cosines Worksheet

5 Key Answers for Algebra 2 Cosines Worksheet
Algebra 2 introduces students to complex trigonometric functions and applications, among which the cosine function holds significant importance. Cosine is fundamental in various mathematical scenarios from wave functions in physics to understanding periodic patterns in real-life phenomena. This blog post will guide you through five key answers related to an Algebra 2 cosines worksheet, helping students grasp these complex concepts with ease.
Understanding the Cosine Function

The cosine function is defined for all real numbers. Here are the key points:
- Definition: Cosine of an angle in a right-angled triangle is the ratio of the adjacent side to the hypotenuse.
- Unit Circle: Cosine values repeat every 360 degrees or 2π radians. On the unit circle, the cosine of an angle θ is the x-coordinate of the point where the terminal side of the angle intersects the circle.
- Equation: cos(θ) = adjacent / hypotenuse
- Graph: Cosine has an amplitude of 1 and a period of 2π, with its graph looking like a smooth wave oscillating between -1 and 1.
🤓 Note: Remember that cosine is an even function; cos(-θ) = cos(θ).
Using Cosine for Triangle Analysis

Cosine can be instrumental in solving for sides and angles in triangles:
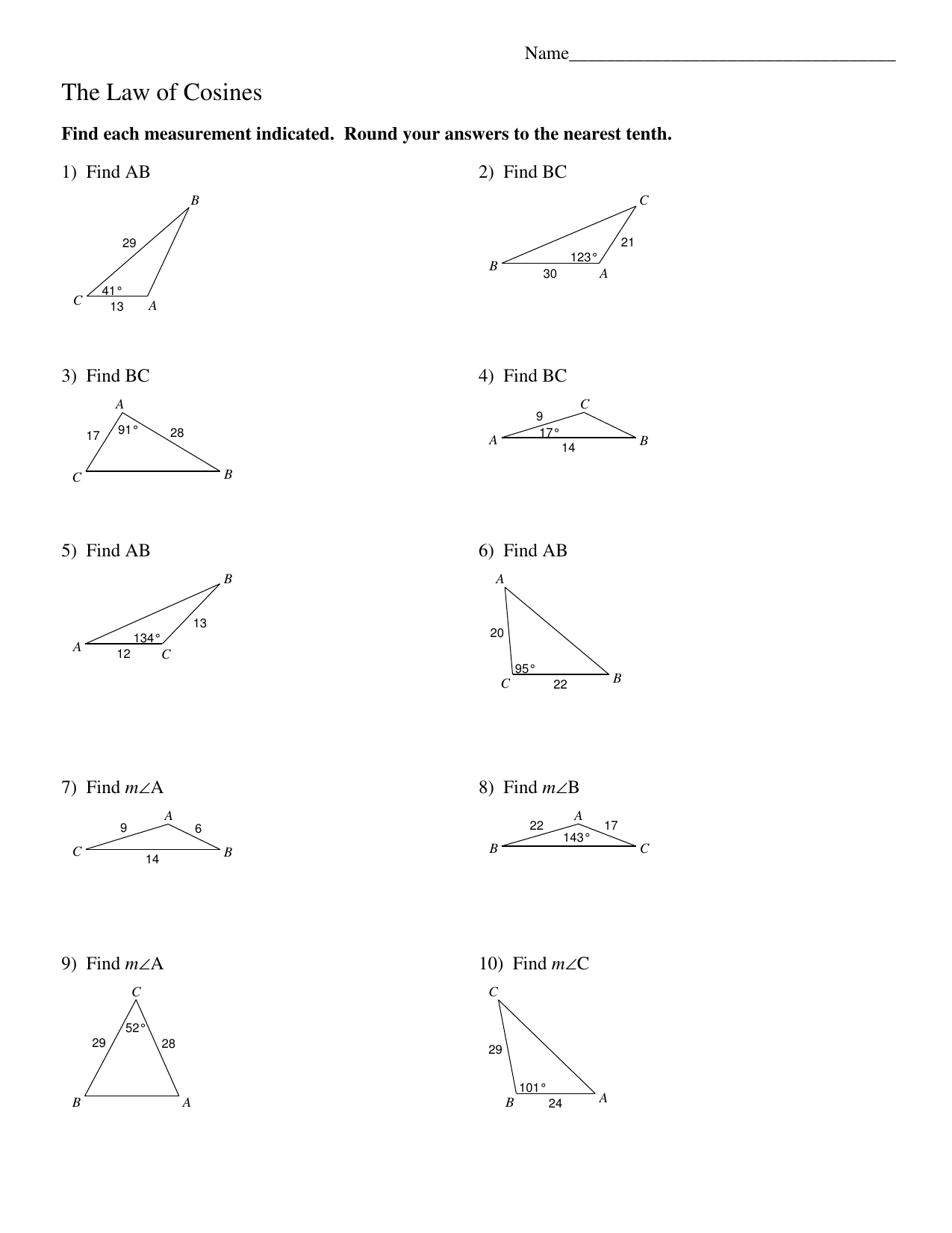
- Law of Cosines: This theorem helps calculate one side of a triangle when the lengths of the other two sides and the included angle are known: \[ c^2 = a^2 + b^2 - 2ab \cdot \cos(C) \]
- Example Calculation: If you know two sides (a = 5, b = 7) and the included angle (C = 45°), solve for the third side (c) using the Law of Cosines: \[ c^2 = 5^2 + 7^2 - 2 \cdot 5 \cdot 7 \cdot \cos(45°) \] \[ c^2 = 74 - 49.497 \] \[ c ≈ \sqrt{24.503} ≈ 4.95 \]
📝 Note: When using a calculator to find cos(45°), make sure your calculator is in degree mode!
Identities Involving Cosine

Trigonometric identities are powerful tools:
- Pythagorean Identity: sin²(θ) + cos²(θ) = 1. This identity holds true for any angle θ.
- Double Angle Formula: cos(2θ) = cos²(θ) - sin²(θ) or 2cos²(θ) - 1
- Sum and Difference Formulas: cos(a ± b) = cos(a)cos(b) ∓ sin(a)sin(b)
Proving Cosine Identities

Proving trigonometric identities using cosines:
- Start with one side of the identity and manipulate it until it matches the other side.
- Use known identities like those above.
- Example: Prove that cos(45° + θ) = cos(θ)cos(45°) - sin(θ)sin(45°): \[ cos(45° + θ) = \frac{\sqrt{2}}{2}cos(θ) - \frac{\sqrt{2}}{2}sin(θ) \]
Solving Cosine Equations

Finding solutions to cosine equations can be both interesting and challenging:
- Basic technique: If cos(x) = k, x = cos-1(k) + 2nπ or -cos-1(k) + 2nπ for all integers n, considering the periodic nature of cosine.
- Example: Solve cos(x) = 0.5 in the interval [0, 2π]: \[ x = cos^{-1}(0.5) = \frac{π}{3} \] or \[ x = 2π - \frac{π}{3} = \frac{5π}{3} \]
🎯 Note: When solving cosine equations, always remember to include the negative cosine angle for a complete solution in the given interval.
In summary, understanding the cosine function in Algebra 2 allows for a deeper comprehension of trigonometric relationships, making it easier to tackle complex problems in mathematics and physics. Whether it's analyzing triangles, using identities, or solving equations, mastering the cosine provides a robust framework for handling trigonometric scenarios effectively. This knowledge not only enhances your mathematical skills but also prepares you for advanced mathematical studies and real-world applications.
What is the difference between sine and cosine?

+
Sine and cosine are both trigonometric functions related to angles in right triangles. The sine of an angle (sin(θ)) is defined as the ratio of the length of the side opposite the angle to the hypotenuse, whereas cosine (cos(θ)) is the ratio of the length of the adjacent side to the hypotenuse. In the context of the unit circle, cosine represents the x-coordinate of the point where the terminal side of the angle intersects the unit circle, while sine represents the y-coordinate.
How can I remember the value of cosine for common angles?

+
One helpful mnemonic is “Some Old Horse Caught Another Horse Taking Oats Away,” which represents the cosine values for angles 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, and 180°. Alternatively, you can memorize the values for the first quadrant (0°, 30°, 45°, 60°, 90°) and understand how they repeat in other quadrants.
Why does the cosine graph oscillate between -1 and 1?
+
The cosine function oscillates because it represents a harmonic motion in trigonometric terms, which is characteristic of sine and cosine functions. These functions are periodic, meaning they repeat their values at regular intervals. The maximum value of cos(θ) is 1 when the angle places the terminal side along the positive x-axis, and the minimum value is -1 when the angle places it along the negative x-axis, covering all values in between as θ increases.