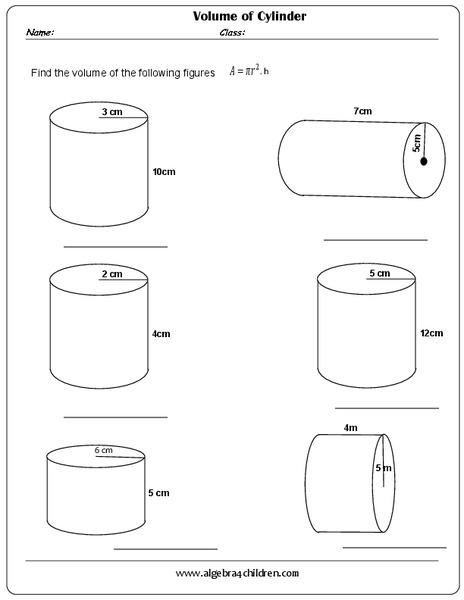
5 Tips for Mastering Quadratic Functions in Algebra 1

Quadratic functions are a fundamental part of algebra, appearing in various fields like physics, economics, and engineering. Understanding how to master these functions can set a strong foundation for higher mathematics. Here are five essential tips to help Algebra 1 students not only understand but excel in dealing with quadratic functions.
Understand the Basics

The journey to mastering quadratic functions begins with understanding their basic structure and behavior. A quadratic function is typically expressed in the standard form:
y = ax2 + bx + c
- a determines the direction and width of the parabola.
- b affects the position of the vertex and the axis of symmetry.
- c is the y-intercept, where the parabola crosses the y-axis.
Understanding how these coefficients change the graph of a quadratic function is crucial:
| Coefficient | Effect on Parabola |
|---|---|
| a > 0 | Parabola opens upward |
| a < 0 | Parabola opens downward |
| |a| > 1 | Parabola narrower |
| 0 < |a| < 1 | Parabola wider |

🧠 Note: Quadratic functions are parabolas because the degree of the polynomial is 2, leading to a unique U-shaped curve.
Solve Quadratic Equations
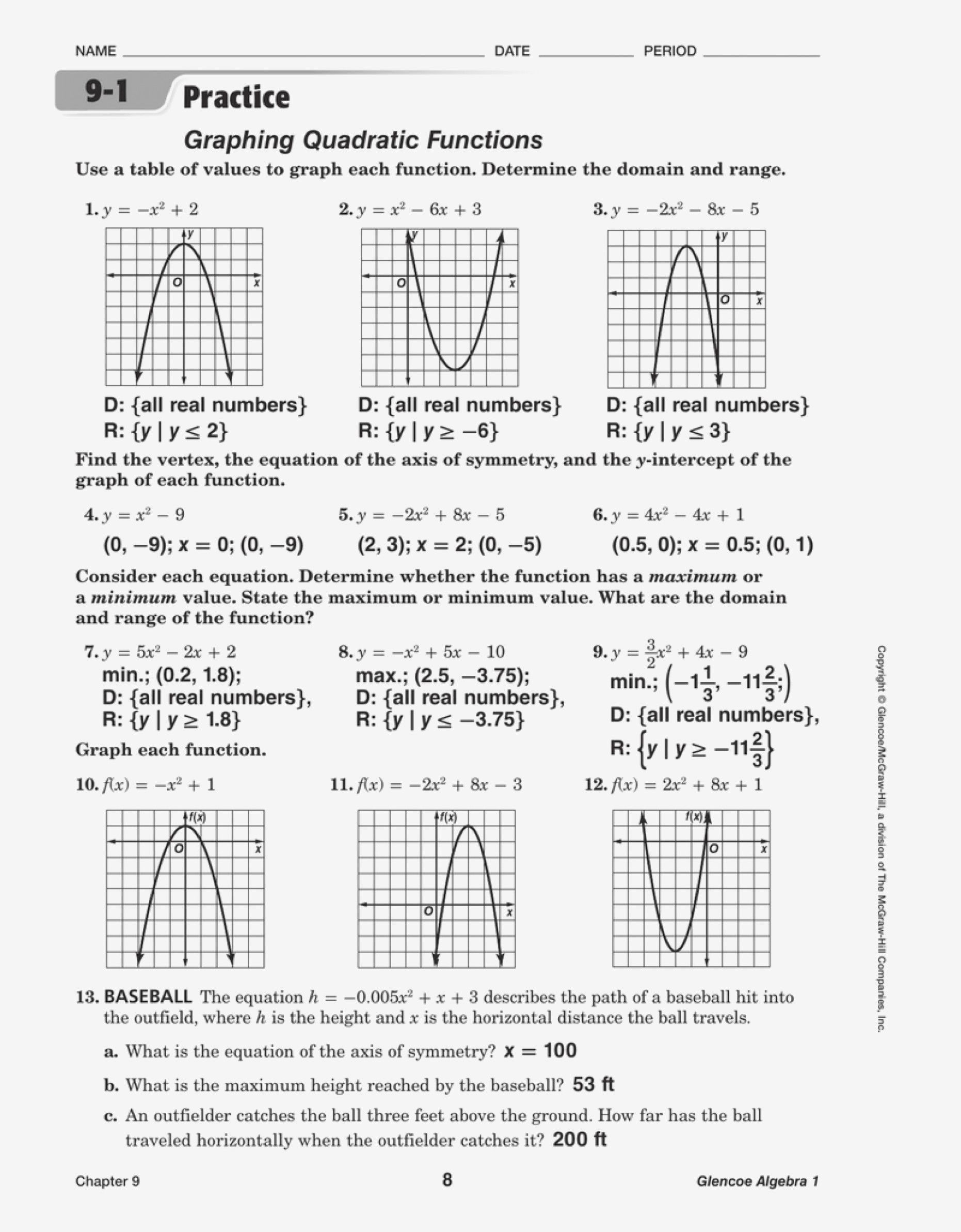
One of the core skills in dealing with quadratic functions is solving them to find the roots. Here are three primary methods:
Factoring

- Identify two numbers that add up to b and multiply to ac.
- Rewrite the middle term using these numbers.
- Factor by grouping.
Quadratic Formula

The universal solution for solving quadratic equations is given by:
x = [-b ± √(b² - 4ac)] / (2a)
- The discriminant b² - 4ac tells about the nature of roots:
- Positive discriminant means two real roots.
- Zero discriminant means one real root (touching the x-axis).
- Negative discriminant means complex roots.
Completing the Square

- Transform the equation into (x + k)2 = c.
- Find k by halving b and squaring it.
- Solve for x.
📝 Note: Practicing all three methods gives you versatility in solving any quadratic equation.
Graphing Quadratic Functions

To graph a quadratic function, you need to:
- Identify the Vertex - The vertex form y = a(x - h)2 + k directly gives the vertex at (h, k).
- Find the Axis of Symmetry - This is given by x = -b / (2a).
- Plot Intercepts - The y-intercept is c from the standard form. Solve for x-intercepts by finding the roots.
- Determine the Direction of Opening - Based on the sign of a.
- Plot Additional Points - Use symmetry to plot points on both sides of the axis of symmetry.
🎨 Note: Graphing helps visualize how changes in coefficients affect the parabola's behavior.
Understand Vertex Form and Factored Form

Besides the standard form, quadratic functions can also be expressed in vertex form or factored form:
Vertex Form

- Form: y = a(x - h)2 + k
- Where (h, k) is the vertex.
- This form directly gives you the transformation (shift or stretch) applied to the parabola.
Factored Form

- Form: y = a(x - r1)(x - r2)
- Where r1 and r2 are the roots of the function.
- Useful for understanding the x-intercepts and solving equations.
Both forms provide different insights into the function:
- Vertex form gives the location of the vertex.
- Factored form provides the roots directly.
Practice, Apply, and Analyze

No amount of theory can replace practical application:
- Practice Problems - Engage in regular problem-solving sessions.
- Real-World Applications - Understand how quadratic functions model real-life scenarios like projectile motion, profit maximization, etc.
- Error Analysis - Learn from mistakes by identifying and understanding common errors.
- Ask for Help - Don't hesitate to seek guidance from teachers or online resources.
- Study in Groups - Collaborative learning often uncovers new ways to approach problems.
By incorporating these strategies, students can significantly enhance their proficiency with quadratic functions.
Ultimately, mastering quadratic functions in Algebra 1 requires a blend of theoretical knowledge, practical application, and continuous learning. Understanding the basic structure, employing various solving methods, graphing effectively, understanding different forms of quadratic functions, and consistent practice are all vital steps in this journey. With dedication and the right approach, quadratic functions will no longer be a daunting topic but an exciting area where mathematics meets the real world.
What is the significance of the discriminant in quadratic equations?

+
The discriminant (b² - 4ac) determines the nature of the roots of a quadratic equation. If it’s positive, you have two distinct real roots; if zero, one real root; and if negative, complex roots.
How does changing the value of ‘a’ affect a quadratic function?

+
Changing the value of ‘a’ alters the parabola’s width and direction. If ‘a’ is positive, the parabola opens upward; if negative, downward. The absolute value of ‘a’ affects how narrow or wide the parabola is.
Why is it beneficial to solve quadratic equations in different forms?

+
Different forms like standard, vertex, or factored provide different insights into the function. Standard form helps in finding intercepts, vertex form directly gives the vertex, and factored form gives the roots, making it easier to solve or graph.