Master Fraction Math: Free Addition & Subtraction Worksheets

Mastering fractions is a fundamental part of mathematical education that can set students up for success in more advanced math topics such as algebra, geometry, and even calculus. This post delves deep into the world of fraction addition and subtraction, providing insights, strategies, and practical tools to help students and educators alike in mastering this core arithmetic operation. Here, we'll explore:
The Essence of Fractions

Fractions are numbers that represent parts of a whole or ratios between two numbers. They are vital for:
- Understanding and measuring quantities accurately in everyday life and in various professional fields.
- Preparing the foundation for more complex mathematical operations and concepts.

Adding and Subtracting Fractions: The Basics

Before tackling addition and subtraction, it’s crucial to understand some basic concepts:
Equivalent Fractions

These are fractions that represent the same value. For example, 1/2 is equivalent to 2/4 or 3/6.
Common Denominator

This is the key to adding or subtracting fractions. The fractions must have a common denominator to be manipulated together.
📝 Note: Always check for the least common denominator (LCD) to make operations simpler.
Improper Fractions and Mixed Numbers

An improper fraction has a numerator equal to or greater than the denominator. A mixed number combines a whole number with a fraction.

Steps to Add and Subtract Fractions

Finding the Common Denominator

Here’s how to find the common denominator:
- Identify the denominators of the fractions.
- Calculate the least common multiple (LCM) of these denominators.
- Adjust the fractions so they all have this common denominator.
| Fractions | Common Denominator | Adjusted Fractions |
|---|---|---|
| 1/2 + 3/4 | 4 | 2/4 + 3/4 |
| 1/3 + 1/4 | 12 | 4/12 + 3/12 |

Adding Fractions

- Add the numerators together.
- Keep the common denominator as the new denominator.
Subtracting Fractions

- Subtract the numerators from one another.
- Keep the common denominator as the new denominator.
📝 Note: Simplify the resulting fraction if possible by dividing both the numerator and the denominator by their greatest common divisor.
Worksheets for Practice

We’ve created a series of free PDF worksheets designed to help with:
- Adding fractions with like and unlike denominators.
- Subtracting fractions with the same and different denominators.
- Converting mixed numbers to improper fractions for easier calculations.
These worksheets are:
- Easy to download: Direct links available for quick access.
- Printable: Perfect for classroom or home practice.
- Comprehensive: Range from simple to complex problems to challenge learners at all levels.

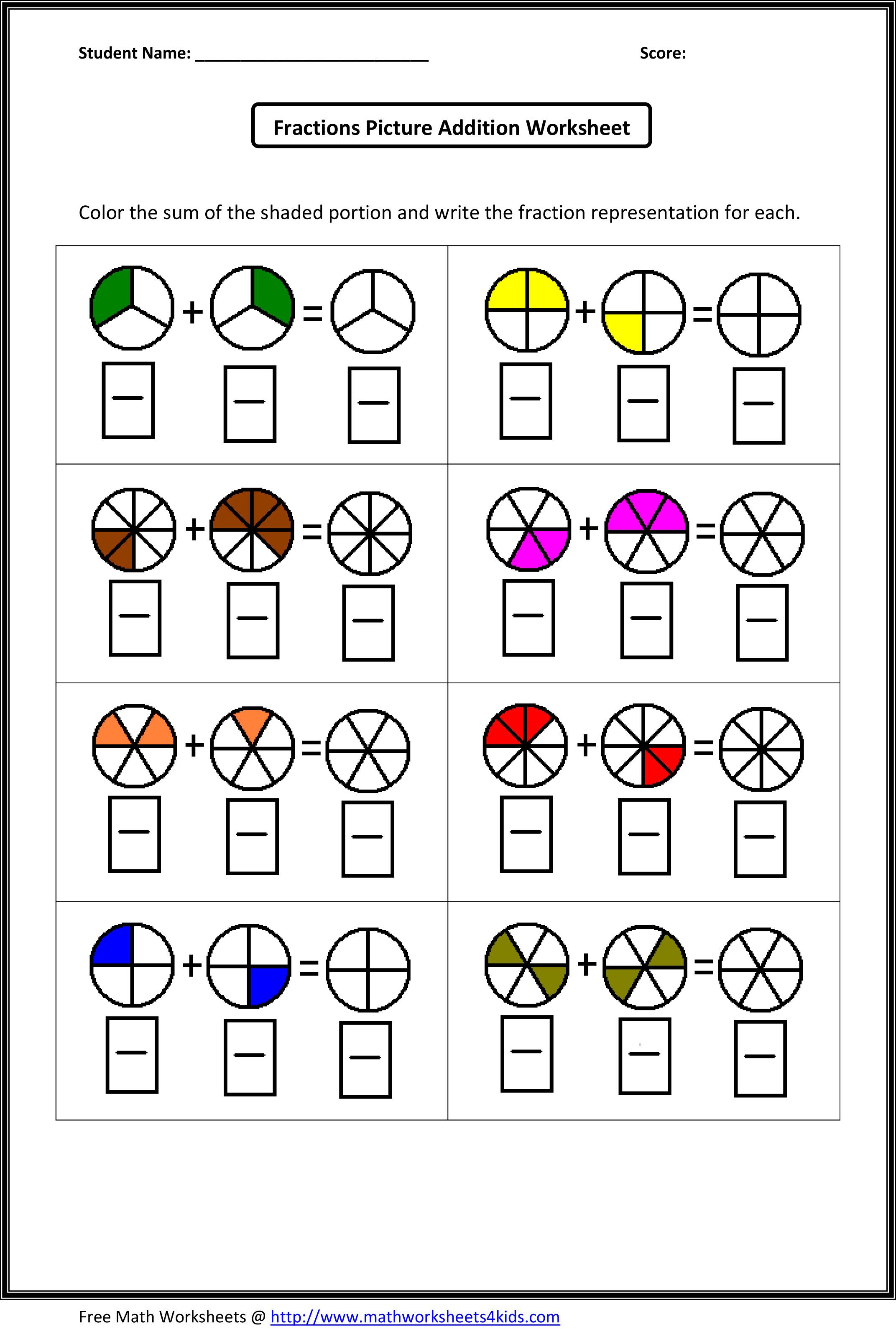
Visual Learning Techniques

Fractions can be abstract, but visual aids like:
- Number Lines: To understand the relative values of fractions.
- Pie Charts: Visual representation of fractions as parts of a whole.
- Bar Models: Helpful in problem-solving and understanding fraction operations.
📝 Note: Encourage students to draw these diagrams to solve problems visually.
Tips for Teachers and Parents

To facilitate learning:
- Use Real-life Scenarios: Cooking, measuring, or dividing items can illustrate fraction operations.
- Incorporate Games: Fraction Bingo, Fraction Wars, or card games can make learning fun.
- Employ Technology: Apps and interactive online tools can provide engaging practice.
In this comprehensive exploration of adding and subtracting fractions, we've covered the essential steps, visual techniques, and resources to help you or your students master this crucial math skill. This process is not just about learning to perform arithmetic operations; it's about understanding the concept of dividing the whole into parts, which is fundamental in both everyday life and advanced mathematical studies. Remember, the journey through fractions is one of building connections, seeing relationships, and using them to solve real-world problems. As you continue to practice with the provided worksheets, encourage the use of visual aids, and make the learning process engaging, you'll pave the way for a deeper understanding of mathematics.
Why do we need to find a common denominator when adding or subtracting fractions?

+
A common denominator allows us to treat fractions as parts of the same whole, which is necessary for operations like addition and subtraction to be meaningful. It makes it possible to directly compare or combine the fractions by giving them a common scale.
What’s the difference between adding fractions and adding mixed numbers?
+
When adding fractions, you directly add the numerators. When adding mixed numbers, you add the whole numbers separately and then deal with the fractional parts, often converting to improper fractions for ease of calculation.
How can visual aids help with learning fractions?

+
Visual aids like pie charts, number lines, and bar models provide a tangible representation of fractions, making abstract concepts more concrete and easier to understand, thus aiding in problem-solving and fostering a deeper understanding.
Can I simplify a fraction before or after adding or subtracting?

+
You can simplify before adding or subtracting by converting the fractions to their simplest forms, but it’s often easier to simplify the result after performing the operation. Simplifying beforehand might complicate finding a common denominator.