5 Ways to Master Scientific Notation Operations

Mastering Scientific Notation Operations: A Comprehensive Guide

Scientific notation is a shorthand way of writing very large or very small numbers. It is widely used in mathematics, physics, engineering, and other fields where numerical calculations are involved. In this article, we will explore five ways to master scientific notation operations, including multiplication, division, addition, and subtraction.
What is Scientific Notation?

Scientific notation is a way of expressing numbers in the form:
a × 10^n
where ‘a’ is a number between 1 and 10, and ‘n’ is an integer. For example, the number 456 can be written in scientific notation as 4.56 × 10^2. Scientific notation is useful for representing very large or very small numbers in a compact and readable form.
1. Multiplication in Scientific Notation
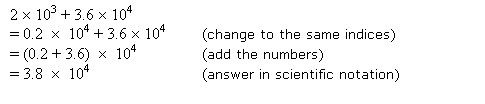
Multiplication in scientific notation is straightforward. When multiplying two numbers in scientific notation, you simply multiply the coefficients (the ‘a’ part) and add the exponents (the ‘n’ part).
Example:
(3 × 10^2) × (4 × 10^3)
= (3 × 4) × 10^(2+3)
= 12 × 10^5
= 1.2 × 10^6
Key Point: When multiplying numbers in scientific notation, make sure to add the exponents.
📝 Note: When multiplying coefficients, the result should be between 1 and 10. If the result is greater than 10, adjust the coefficient and exponent accordingly.
2. Division in Scientific Notation

Division in scientific notation is similar to multiplication. When dividing two numbers in scientific notation, you simply divide the coefficients and subtract the exponents.
Example:
(6 × 10^4) ÷ (2 × 10^2)
= (6 ÷ 2) × 10^(4-2)
= 3 × 10^2
Key Point: When dividing numbers in scientific notation, make sure to subtract the exponents.
📝 Note: When dividing coefficients, the result should be between 1 and 10. If the result is less than 1, adjust the coefficient and exponent accordingly.
3. Addition and Subtraction in Scientific Notation
Addition and subtraction in scientific notation are more complex than multiplication and division. When adding or subtracting numbers in scientific notation, you need to ensure that the exponents are the same.
Example:
(2 × 10^3) + (4 × 10^2)
First, adjust the numbers to have the same exponent:
(2 × 10^3) + (0.4 × 10^3)
= (2 + 0.4) × 10^3
= 2.4 × 10^3
Key Point: When adding or subtracting numbers in scientific notation, make sure the exponents are the same before performing the operation.
📝 Note: When adding or subtracting coefficients, the result should be between 1 and 10. If the result is greater than 10, adjust the coefficient and exponent accordingly.
4. Converting Between Standard Notation and Scientific Notation

Converting between standard notation and scientific notation is an essential skill. To convert from standard notation to scientific notation, move the decimal point to the left until you have a number between 1 and 10, then multiply by 10 raised to the power of the number of places you moved the decimal point.
Example:
456 → 4.56 × 10^2
To convert from scientific notation to standard notation, multiply the coefficient by 10 raised to the power of the exponent.
Example:
4.56 × 10^2 → 456
5. Real-World Applications of Scientific Notation

Scientific notation has numerous real-world applications in fields such as physics, engineering, and mathematics. For example, scientists use scientific notation to express the speed of light (3 × 10^8 meters per second) and the size of atoms (on the order of 10^-10 meters).
Table: Real-World Applications of Scientific Notation
| Field | Example |
|---|---|
| Physics | Speed of light: 3 × 10^8 meters per second |
| Engineering | Size of atoms: on the order of 10^-10 meters |
| Mathematics | Large numbers: 10^100 |

In conclusion, mastering scientific notation operations is essential for anyone working with large or small numbers. By understanding the basics of scientific notation and practicing multiplication, division, addition, and subtraction, you can become proficient in using this notation system. Remember to convert between standard notation and scientific notation, and apply your knowledge to real-world problems.
What is scientific notation?

+
Scientific notation is a way of expressing numbers in the form a × 10^n, where ‘a’ is a number between 1 and 10, and ‘n’ is an integer.
How do you multiply numbers in scientific notation?

+
When multiplying numbers in scientific notation, multiply the coefficients and add the exponents.
How do you convert between standard notation and scientific notation?

+
To convert from standard notation to scientific notation, move the decimal point to the left until you have a number between 1 and 10, then multiply by 10 raised to the power of the number of places you moved the decimal point. To convert from scientific notation to standard notation, multiply the coefficient by 10 raised to the power of the exponent.



