5 Easy Ways to Solve Pythagorean Theorem Problems

The Pythagorean Theorem is a foundational principle in geometry that has intrigued minds for over 2500 years. Whether you're a student in high school, a budding mathematician, or simply someone with a passion for puzzles, understanding and applying the Pythagorean Theorem can unlock a world of mathematical possibilities. Here are 5 easy ways to master this fundamental theorem, ensuring that solving Pythagorean problems becomes second nature.
Understand the Basics

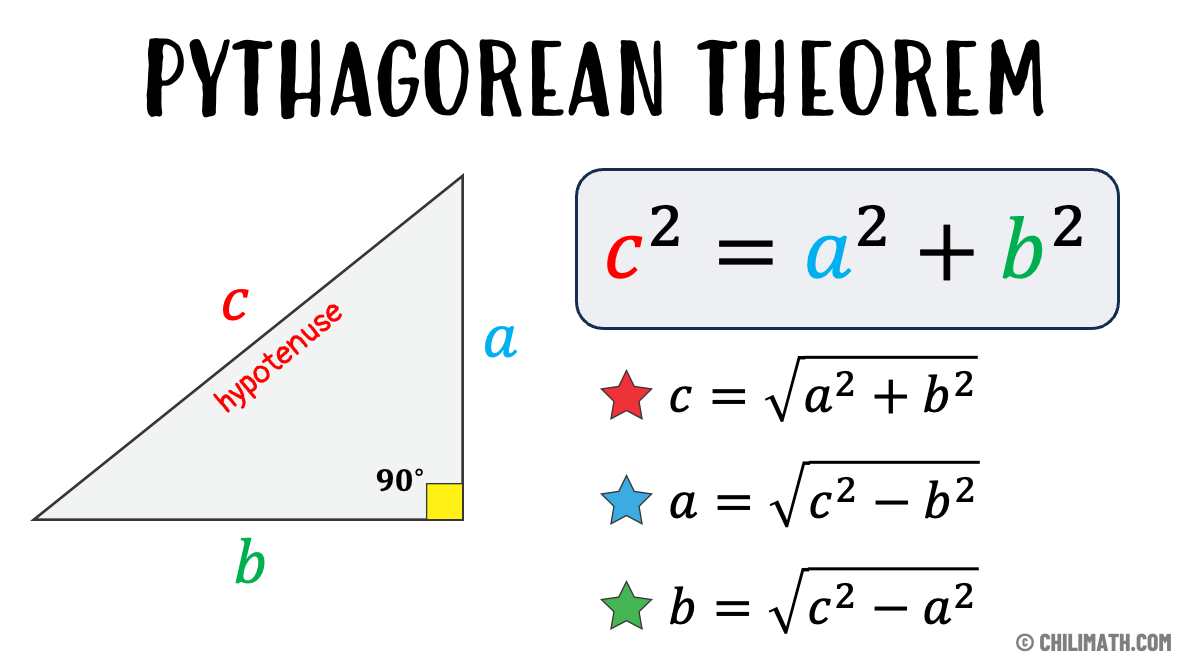
Before diving into complex problem-solving, it’s crucial to get a firm grip on what the Pythagorean Theorem really says. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b). This can be expressed with the simple formula:
c² = a² + b²This equation allows you to find any of the three sides given the lengths of the other two.
🔍 Note: Remember that this formula applies only to right-angled triangles. If your triangle isn't a right angle, this equation won't hold true.
Practice with Simple Examples
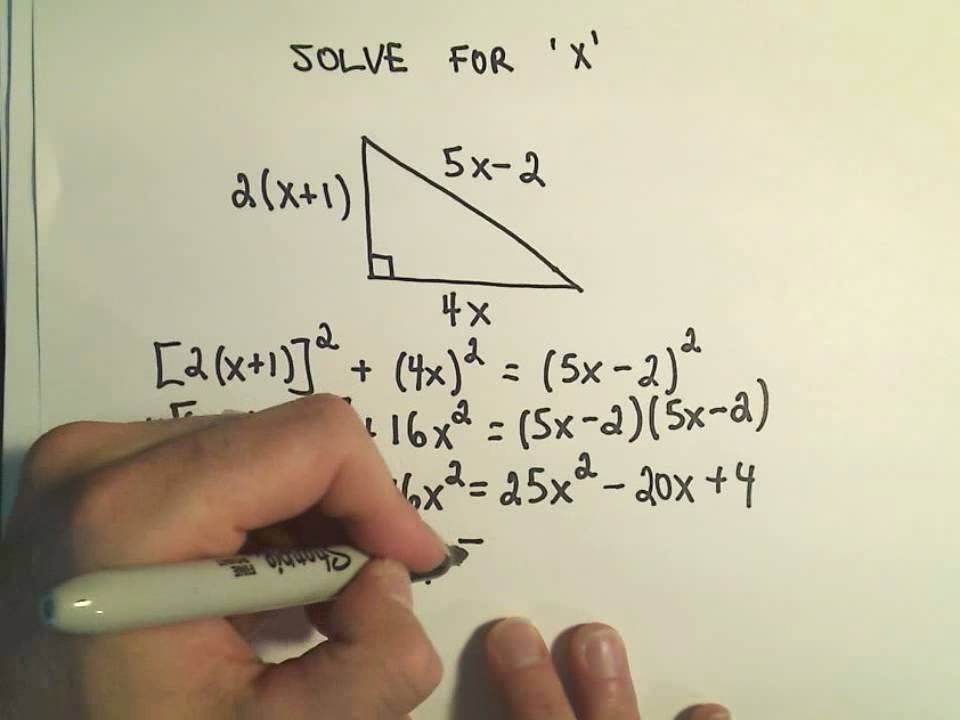
- Identify a Triangle: Start with a triangle where you know two sides are 3 units and 4 units.
- Calculate the Hypotenuse: Use the Pythagorean formula to find the length of the hypotenuse:
5² = 3² + 4² - Square the Result: Square both sides to get:
25 = 9 + 16 - Determine the Hypotenuse: Since both sides are equal, the hypotenuse is √25 = 5 units.
📚 Note: Practicing with familiar and simple numbers helps solidify your understanding of the theorem's application.
Recognize Common Pythagorean Triples
| Side ‘a’ | Side ‘b’ | Hypotenuse ‘c’ |
|---|---|---|
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 7 | 24 | 25 |
| 8 | 15 | 17 |
| 9 | 40 | 41 |

Being familiar with Pythagorean triples can save time. These are sets of positive integers, (a, b, c), such that a² + b² = c². Knowing these can help you instantly recognize solutions without complex calculations.
🧠 Note: Memorizing or at least recognizing these triples can give you an intuitive advantage when solving problems quickly.
Work with Real-World Examples

Applying the Pythagorean Theorem in real-life scenarios not only makes learning fun but also helps in visualizing its practical application:
- Finding Ladder Length: If you need a ladder to reach 9 meters up a wall, and it's placed 5 meters from the wall, how long must the ladder be?
- Side a = 5m (distance from wall)
- Side b = 9m (height up the wall)
- c² = 5² + 9² = 106
- The ladder should be at least √106 ≈ 10.3 meters long.
- Navigation: In navigation, pilots or captains might use the theorem to find the shortest distance between two points on a map, known as the 'great circle distance'.
Explore Variations and Extensions

Once you’ve got the basics down, dive into more advanced concepts:
- Generalize the Theorem: Consider what happens in different geometries or with trigonometric identities.
- Pythagorean Theorem in Three Dimensions: Explore how the theorem extends into 3D space by considering surfaces and solids.
- Proofs: There are numerous proofs for the Pythagorean Theorem. Learning a few, like the geometric proof using similar triangles, can provide deeper insights.
🔎 Note: Exploring these variations not only reinforces your understanding but also enriches your problem-solving toolkit.
Through these five methods, you'll find that the Pythagorean Theorem becomes less about memorizing a formula and more about understanding the underlying principles of geometric relationships. By grasping the basics, practicing with examples, recognizing triples, applying real-world scenarios, and exploring further, you'll be well-equipped to tackle even the most challenging problems with confidence. This journey through the Pythagorean Theorem not only enhances your mathematical skills but also highlights the beauty and interconnectedness of mathematical concepts.
Why is it called the Pythagorean Theorem?

+
The theorem is named after the Greek mathematician Pythagoras, although the concept predates him. It was attributed to him because he and his school were among the first to provide a systematic proof of this mathematical principle.
Can the Pythagorean Theorem be used for non-right angled triangles?

+
No, the Pythagorean Theorem applies exclusively to right-angled triangles. For other triangles, you would use the Law of Cosines, which generalizes the theorem for any triangle.
How does the theorem help in real life?

+
The Pythagorean Theorem has countless applications, from navigation and architecture to computer graphics. It helps determine distances, construct buildings, design video games, and much more, showcasing its significance in both theoretical and applied sciences.



