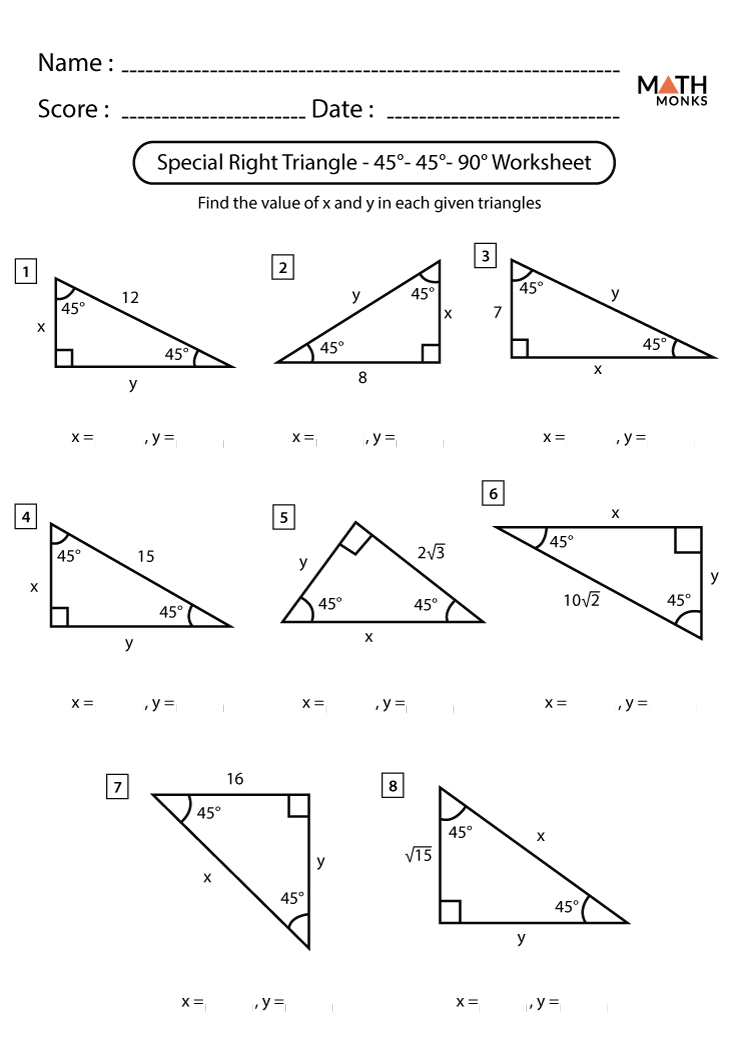
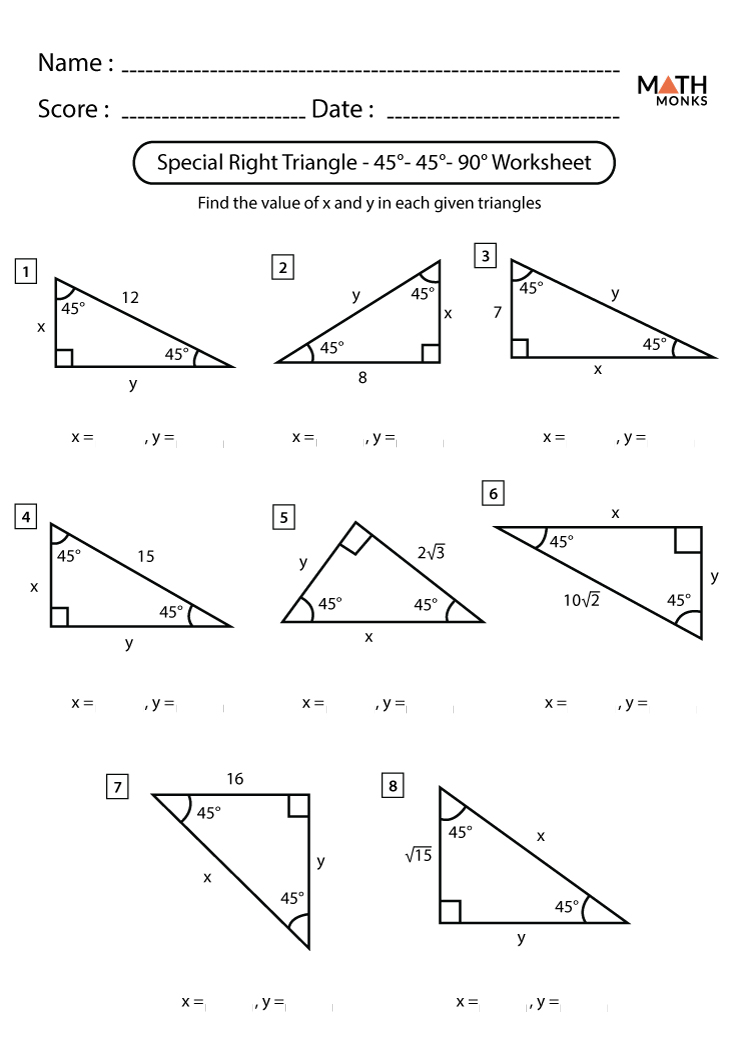
8.2 Special Right Triangles Worksheet Answers Revealed

In the realm of geometry, understanding the intricacies of special right triangles can unlock a world of possibilities, from engineering precise architectural structures to crafting complex mathematical proofs. If you're grappling with the fine details of isosceles right triangles and 30-60-90 triangles, this guide will illuminate the answers to your 8.2 Special Right Triangles Worksheet, ensuring you not only memorize but truly understand these fundamental shapes.
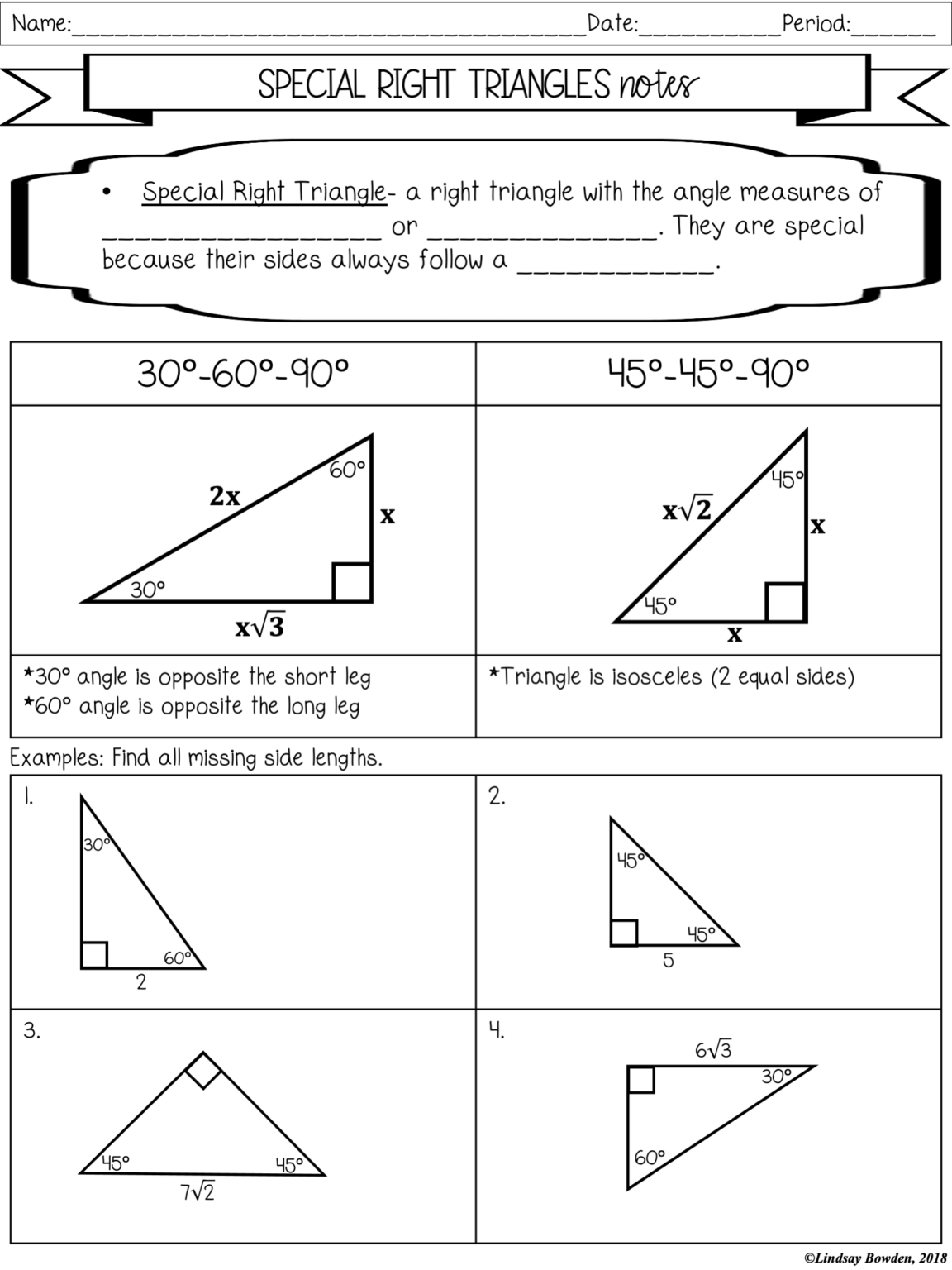
The Essence of Special Right Triangles

Before we delve into the worksheet answers, let's ground ourselves in what makes these triangles special:
- Isosceles Right Triangle: This triangle, known for its two equal sides and a right angle, adheres to the ratio of sides as 1 : 1 : √2.
- 30-60-90 Triangle: Here, the ratio is 1 : √3 : 2, with the smallest angle at 30°.
Understanding these ratios is pivotal when working through your worksheet. Now, let's reveal the answers to those questions, with each solution accompanied by the underlying mathematical reasoning.
Worksheet Answers

The following table compiles answers for typical questions found in 8.2 Special Right Triangles Worksheets, providing a clear look at how to approach these problems:
| Question | Answer | Reasoning |
|---|---|---|
| 1. In an isosceles right triangle, if the legs are 4 units each, what is the length of the hypotenuse? | 4√2 units | The hypotenuse in an isosceles right triangle is leg x √2. |
| 2. For a 30-60-90 triangle with a short leg of 5 units, calculate the other two sides. | Longer leg: 5√3 units, Hypotenuse: 10 units | The ratios for a 30-60-90 triangle are 1 : √3 : 2. Thus, short leg = 5, longer leg = 5√3, and hypotenuse = 2x5 = 10. |
| 3. If the hypotenuse of an isosceles right triangle is 8 units, find the length of each leg. | 4√2 units each | Using the relationship leg = hypotenuse / √2, each leg is 8 / √2 = 8√2 / 2 = 4√2 units. |

🔍 Note: It's beneficial to memorize these ratios as they are the key to solving such problems efficiently.
The above examples not only give you the answers but also guide you through the logic and mathematical foundations behind each calculation. This approach ensures a deeper understanding, making you adept at tackling these triangles in various contexts.
As we move forward, remember that these triangles are not only interesting from an academic standpoint but also crucial for real-world applications. From designing building structures to analyzing forces in physics, the principles of special right triangles are everywhere. By mastering these shapes, you're not just answering worksheet problems but unlocking the door to a wider world of mathematical applications.
Real-World Applications
- Architecture: Special right triangles help in constructing stable roof structures and calculating the correct angles for support beams.
- Physics: They're essential for understanding vector components, force resolution, and the mechanics of inclined planes.
- Navigation: Sailors and pilots often use these triangles to chart courses, ensuring precise angles and distances.
🔍 Note: The practical application of these triangles extends beyond the classroom, making them indispensable for many professions.
Beyond the Worksheet
When you're not busy working through worksheets, there are numerous ways to deepen your understanding of special right triangles:
- Mathematical Proofs: Explore and write proofs demonstrating the properties of these triangles.
- Interactive Tools: Use geometry software or apps to manipulate these triangles virtually, observing how changes in side lengths affect angles and ratios.
- Visual Representation: Sketch or build models of these triangles to understand their visual attributes better.
The journey of mastering special right triangles is one of discovery. With each problem you solve and each application you understand, you're not just learning formulas; you're equipping yourself with a powerful tool in your mathematical arsenal. The answers provided here are a stepping stone to a broader and more profound appreciation of geometry.
Why are these triangles called ‘special’?
+
These triangles are called ‘special’ because of their unique side length ratios and angle measures, which provide predictable and easily calculable dimensions. These ratios simplify many geometric calculations.
How do these triangles relate to the Pythagorean Theorem?

+
The Pythagorean Theorem (a² + b² = c²) is fundamental in proving the relationships within these triangles. The special ratios can be derived from this theorem, making these triangles particularly useful in practical applications where precision is crucial.
Are there any other types of ‘special’ triangles?
+
Yes, besides isosceles right and 30-60-90 triangles, there are other triangles with unique properties like the 45-45-90 triangle, which is similar to the isosceles right triangle but with a different ratio. There are also less common triangles like the 5-12-13 or 8-15-17 triangles, which are Pythagorean triples.