5 Simple Tricks to Solve Exponents Easily

Understanding how to simplify and solve exponents can significantly enhance your mathematical prowess, be it for academic purposes, competitive exams, or even practical applications in daily life. This blog post explores five simple yet effective tricks that can make exponentiation not just easy but also enjoyable.
Understanding Exponent Basics

Before we dive into the tricks, it’s vital to have a firm grasp on what exponents are and how they function.
- Definition: An exponent or power signifies how many times a number, called the base, is multiplied by itself.
- Example: In 34, the base is 3, and the exponent is 4, so 34 = 3 × 3 × 3 × 3 = 81.
📝 Note: Exponents are often referred to as powers or indices.
Trick #1: Power of Zero

One of the fundamental rules of exponents is that any number raised to the power of zero is equal to 1.
- Example: 50 = 1, (-7)0 = 1, π0 = 1
This rule helps in simplifying expressions involving zero powers, making them a quick step in solving problems.
Trick #2: Negative Exponents

Negative exponents indicate division rather than multiplication. To convert a negative exponent to a positive one:
- Example: x-n = 1/xn
- Tip: This trick is particularly useful for simplifying fractions where exponents appear in the denominator.
⚠️ Note: When dealing with negative exponents, the sign of the exponent changes upon division.
Trick #3: Multiplying Exponents with the Same Base
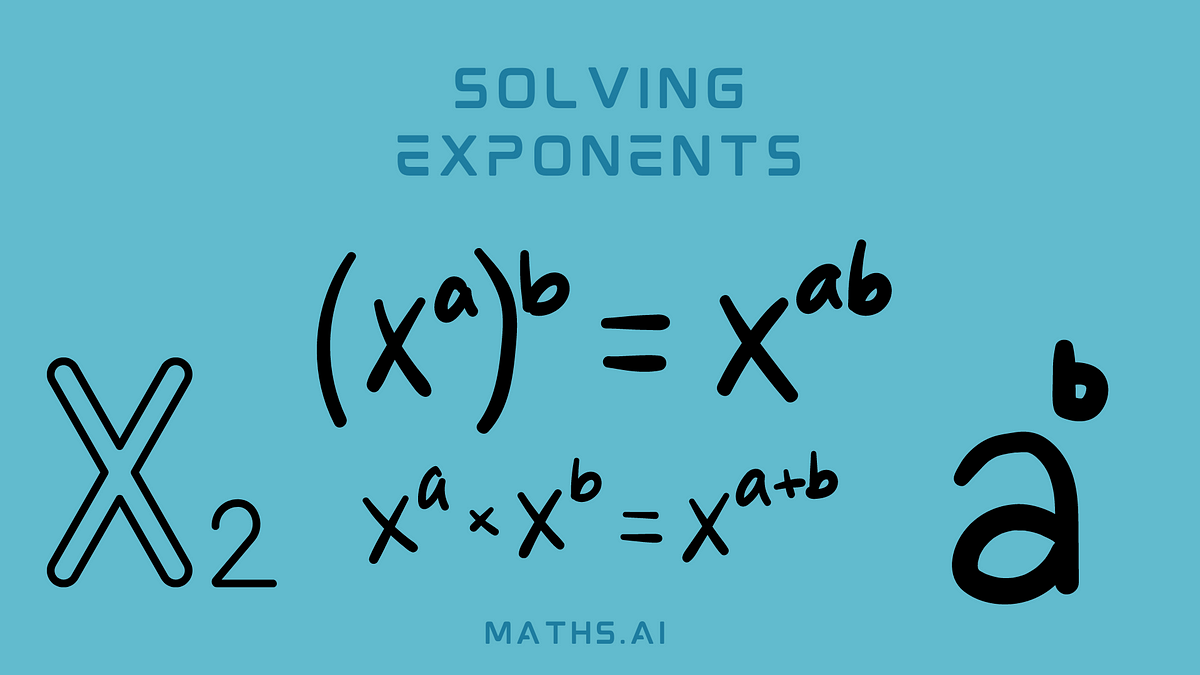
When multiplying numbers with the same base, you add their exponents.
- Example: a3 * a4 = a3+4 = a7
- This simplifies the multiplication process immensely.
Trick #4: Dividing Exponents with the Same Base

Similar to multiplication, when dividing numbers with the same base, you subtract their exponents.
- Example: a8 / a5 = a8-5 = a3
This trick is helpful for simplifying expressions with fractions.
Trick #5: Exponent Power Rule

When raising a power to another power, you multiply the exponents.
- Example: (a3)4 = a3*4 = a12
This rule simplifies complex exponent expressions efficiently.
🔎 Note: Recognizing and applying these patterns can drastically reduce the complexity of your calculations.
In summary, these five tricks provide a robust foundation for tackling exponents with ease. By understanding and applying the power of zero, negative exponents, exponent multiplication, division, and the power of powers, you can navigate through complex mathematical scenarios with confidence. With practice, these principles will not only speed up your calculations but also deepen your mathematical intuition.
What happens when the base of an exponent is negative?

+
If the base of an exponent is negative, the result depends on whether the exponent is even or odd. An odd exponent keeps the base’s sign: (-2)3 = -8, whereas an even exponent results in a positive value: (-2)2 = 4.
Can these exponent rules be used with variables?

+
Yes, these rules apply to variables just as they do to numbers, provided the variables represent the same base. For example, x3 * x2 = x5.
How do you simplify an exponent to a zero power?

+
Any number or variable raised to the power of zero equals 1. For instance, 50 = 1, x0 = 1 for any x except 0.