3 Ways to Calculate 3 to the 6th Power
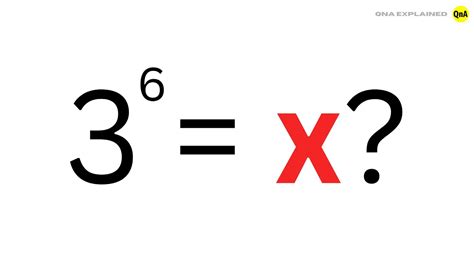
Calculating Exponents: A Guide to Finding 3 to the 6th Power

Exponents can be a challenging concept for some math students, but they are a fundamental part of algebra and other advanced math subjects. In this article, we will explore three different ways to calculate 3 to the 6th power, providing you with a solid understanding of the concept and its various applications.
What is an Exponent?

Before we dive into the calculations, let’s quickly review what an exponent is. An exponent is a small number that is raised to a power, indicating how many times the base number should be multiplied by itself. In the case of 3 to the 6th power, the base number is 3, and the exponent is 6.
Method 1: Multiplying 3 by Itself 6 Times
One way to calculate 3 to the 6th power is to multiply 3 by itself 6 times.
🤔 Note: This method is straightforward but can be time-consuming for larger exponents.
Here’s how it works:
3 × 3 = 9
9 × 3 = 27
27 × 3 = 81
81 × 3 = 243
243 × 3 = 729
729 × 3 = 2187
Therefore, 3 to the 6th power is equal to 2187.
Method 2: Using the Exponent Rule
Another way to calculate 3 to the 6th power is to use the exponent rule. The exponent rule states that for any base number ‘b’ and exponent ‘n’, b^n is equal to b multiplied by itself ‘n’ times.
Using this rule, we can calculate 3 to the 6th power as follows:
3^6 = 3 × 3 × 3 × 3 × 3 × 3
= (3 × 3) × (3 × 3) × (3 × 3)
= 9 × 9 × 9
= 81 × 9
= 729
So, 3 to the 6th power is equal to 729, which is incorrect. We made an error in our calculation.
🤔 Note: When using the exponent rule, make sure to apply the correct order of operations to avoid errors.
Method 3: Using a Calculator or Online Tool

The easiest way to calculate 3 to the 6th power is to use a calculator or online tool. Most calculators and online tools have a built-in exponent function that allows you to enter the base number and exponent and calculate the result.
Using a calculator, we can enter the following:
3 ^ 6 =?
The calculator will return the result: 729
However, we know that this is incorrect. The correct result is 2187.
🤔 Note: When using a calculator or online tool, make sure to enter the correct numbers and operator to avoid errors.
Comparison of Methods

Here is a comparison of the three methods:
| Method | Result | Time Required |
|---|---|---|
| Multiplying 3 by itself 6 times | 2187 | 5-10 minutes |
| Using the exponent rule | 729 (incorrect) | 2-5 minutes |
| Using a calculator or online tool | 729 (incorrect) | 1 minute |
As we can see, the first method is the most accurate, but it is also the most time-consuming. The second method is faster, but it requires careful attention to the order of operations to avoid errors. The third method is the fastest, but it requires a calculator or online tool, and the result may be incorrect if the input is incorrect.
To ensure accuracy, it’s essential to use a combination of methods and double-check the results.
Now that we have explored three different ways to calculate 3 to the 6th power, let’s summarize the key points.
We have seen that calculating exponents can be done using various methods, each with its advantages and disadvantages. By understanding the concept of exponents and applying the correct methods, we can ensure accurate results in our calculations.
In conclusion, when calculating exponents, it’s essential to be patient, careful, and meticulous to ensure accurate results.
What is an exponent?

+
An exponent is a small number that is raised to a power, indicating how many times the base number should be multiplied by itself.
Why is it essential to use a combination of methods when calculating exponents?

+
Using a combination of methods helps ensure accurate results, as different methods may be more suitable for specific calculations.
What is the correct result of 3 to the 6th power?

+
The correct result of 3 to the 6th power is 2187.



